P4747 [CERC2017] Intrinsic Interval 题解

题目链接：Intrinsic Interval

讲讲析合树如何解决这种问题，其实这题很接近析合树的板题的应用。

增量法进行析合树建树时，需要用 ST 表预处理出 \(max\) 和 \(min\) 以便 \(O(1)\) 查询极差，然后线段树去维护 \([l,r]\) 上的极差减区间端点做差即 \(diff-(r-l)\)，当这玩意等于 \(0\) 时容易知道，\([l,r]\) 就是一个连续段，而我们观察到这个东西是 \(\ge 0\) 的，很容易证的，区间极差一定大于等于端点做差。因为这个是排列，所以一定最多有 \(r-l\) 个连续的数，这样使得极差至少都是 \(r-l\)，不会小于它。所以我们线段树维护个区间最小值，当然因为还有增量变化，所以再维护个区间加操作，这玩意是单调不升的，就能线段树上二分出 \(L_i\)，这个 \(L_i\) 是使得 \([L_i,curr]\) 为连续段的最左边的点，显而易见的，我们需要用当前节点 \(curr\) 不断向左合并一直到这个节点为止。

考虑每次加入一个节点对线段树维护有何影响，容易观察到如果 \(max\) 变大了，那么显然需要去掉原来的 \(max\) 加入新的 \(max\)，\(min\) 只有可能变小，那么很显然原来极差是 \(max-min\)，此时应该加上原来的 \(min\) 减去新的 \(min\) 即可。这个最大最小值变化只需要维护单调栈就行了，维护单调递增和递减栈。相邻的栈节点他们的最大或者最小值是相同的，加入了新的节点使得被弹出了，这个时候就更改了相邻节点的最大最小值，这个时候就需要更改它们的线段树贡献了。

加入这个节点构成析合森林就老规矩，三种情况分讨：

1. 这个栈顶节点是合点，且可以和它的最右儿子的左端点区间形成连续段，符合合点性质，直接作为这个栈顶节点的右儿子。

2. 本身可以和它作为一个连续段，那就构造一个新的节点作为合点，作为它俩的父亲就行了。

3. 这个时候需要一堆节点合并成一个新的连续段，新搞一个根，然后不断地弹栈找到这个形成连续段的点，这一堆点不符合合点相邻形成连续段的性质，所以这一堆连续段合并起来的新节点是一个析点。

注意往右添加移动 \([l,r]\) 中的 \(r\)，时，显然 \(diff-(r-l)\) 整体会 \(-1\)，注意去掉就行。

这样一来析合树就建完了。

本题做法

很显然的是，查询区间的两个端点的 \(lca\) 即是满足的一个连续段，但它不一定是答案说的包含这个区间的 “最小” 连续段。具体的分讨：

1. 如果这个 \(lca\) 是析点，显然析点对应的区间就是答案了，因为析点的相邻子节点并不能拼成连续段，只能由所有节点拼凑。

2. 如果这个 \(lca\) 是合点，显然根据合点的性质，它的任意相邻儿子可以拼成连续段，我们只需要找到这两个对应的到 \(lca\) 链上的两个相邻子区间形成的连续段更小。

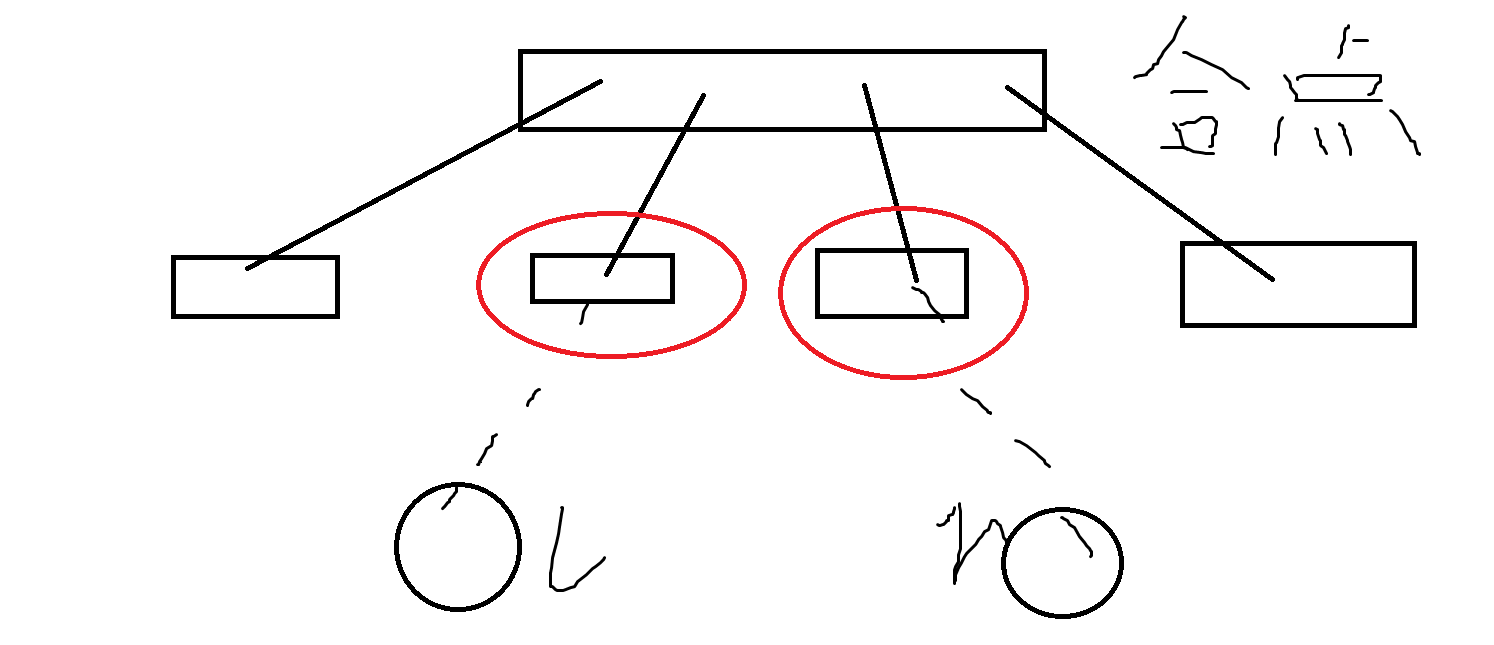
如图，\(l\) 和 \(r\) 对应的最小连续段应该为红色圆圈两个连续段的组合才是答案。所以倍增找到 \(lca\) 深度 \(+1\) 的那个点就行了，具体的相当于找 \(k\) 级祖先，找到 \(deep[l/r]-deep[lca]-1\) 级祖先即是这个点。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize("Ofast,unroll-loops")
// #pragma GCC optimize(2)

// #define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}

template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 2e5 + 10;
constexpr int T = 25;
int a[N], n;

//查询极差
struct
{
    int stMin[N][T], stMax[N][T];
    int LOG2[N];

    void build()
    {
        forn(i, 2, n)LOG2[i] = LOG2[i >> 1] + 1;
        const int k = LOG2[n] + 1;
        forn(i, 1, n)stMax[i][0] = stMin[i][0] = a[i];
        forn(j, 1, k)
        {
            forn(i, 1, n-(1<<j)+1)
            {
                stMin[i][j] = min(stMin[i][j - 1], stMin[i + (1 << j - 1)][j - 1]);
                stMax[i][j] = max(stMax[i][j - 1], stMax[i + (1 << j - 1)][j - 1]);
            }
        }
    }

    int queryRange(const int l, const int r) const
    {
        const int k = LOG2[r - l + 1];
        return max(stMax[l][k], stMax[r - (1 << k) + 1][k]) - min(stMin[l][k], stMin[r - (1 << k) + 1][k]);
    }
} ST;

//是否是连续段
inline bool isContinue(const int l, const int r)
{
    return ST.queryRange(l, r) == r - l;
}

//维护Diff-(r-l)最小值(单调递增),线段树上二分找第一个为0的点,即为最近第一个满足点
struct
{
    struct Node
    {
        int Min, Add;
    } node[N << 2];

#define Min(x) node[x].Min
#define Add(x) node[x].Add

    void push_up(const int curr)
    {
        Min(curr) = min(Min(ls(curr)),Min(rs(curr)));
    }

    void push_down(const int curr)
    {
        if (Add(curr))
        {
            Min(ls(curr)) += Add(curr), Min(rs(curr)) += Add(curr);
            Add(ls(curr)) += Add(curr), Add(rs(curr)) += Add(curr);
            Add(curr) = 0;
        }
    }

    void add(const int curr, const int l, const int r, const int val, const int s = 1, const int e = n)
    {
        if (l <= s and e <= r)
        {
            Min(curr) += val, Add(curr) += val;
            return;
        }
        const int mid = s + e >> 1;
        push_down(curr);
        if (l <= mid)add(ls(curr), l, r, val, s, mid);
        if (r > mid)add(rs(curr), l, r, val, mid + 1, e);
        push_up(curr);
    }

    int query(const int curr = 1, const int l = 1, const int r = n)
    {
        const int mid = l + r >> 1;
        if (l == r)return l;
        push_down(curr);
        if (!Min(ls(curr)))return query(ls(curr), l, mid);
        return query(rs(curr), mid + 1, r);
    }
} Seg;

//析合树节点
struct DCT
{
    int type, left, right, rightL; //0是析点,1是合点
    DCT() = default;

    DCT(const int left, const int right, const int type = 0, const int rightL = 0)
        : type(type),
          left(left),
          right(right), rightL(rightL)
    {
    }
} dct[N];

int dctRoot;
#define left(x) dct[x].left
#define right(x) dct[x].right
#define type(x) dct[x].type
#define rightL(x) dct[x].rightL
int cnt;
int stMax[N], stMin[N], maxCnt, minCnt; //两种单调栈
stack<int> st; //析合森林节点
#define maxTop a[stMax[maxCnt]]
#define minTop a[stMin[minCnt]]
#define root st.top()
vector<int> child[N]; //析合树邻接表
int node[N]; //每个点所在析合树节点编号
//维护为(Max-Min)-(r-l)>=0,去Max需要减,取Min则是加
inline void build()
{
    forn(i, 1, n)
    {
        while (maxCnt and a[i] >= maxTop)Seg.add(1, stMax[maxCnt - 1] + 1, stMax[maxCnt], -maxTop), maxCnt--;
        while (minCnt and a[i] <= minTop)Seg.add(1, stMin[minCnt - 1] + 1, stMin[minCnt], minTop), minCnt--;
        Seg.add(1, stMax[maxCnt] + 1, i, a[i]), Seg.add(1, stMin[minCnt] + 1, i, -a[i]);
        stMax[++maxCnt] = stMin[++minCnt] = i;
        dct[node[i] = ++cnt] = DCT(i, i);
        const int L = Seg.query();
        int curr = cnt;
        //需要将这个连续段的所有本原连续段的节点解决了
        while (!st.empty() and left(root) >= L)
        {
            if (type(root) and isContinue(rightL(root), i))
            {
                //合点且最后一个点可以和当前点形成连续段,所以做儿子
                right(root) = i;
                rightL(root) = left(curr);
                child[root].push_back(curr);
                curr = root;
                st.pop();
            }
            else if (isContinue(left(root), i))
            {
                //本身和它连续就合并节点成为合点
                dct[++cnt] = DCT(left(root), i, 1,left(curr)); //构造新的合点,当前节点就是最右节点,栈顶则是左节点
                child[cnt].push_back(root);
                child[cnt].push_back(curr);
                st.pop();
                curr = cnt;
            }
            else
            {
                //不断合并往左找连续段
                child[++cnt].push_back(curr);
                do child[cnt].push_back(root), st.pop();
                while (!isContinue(left(root), i));
                dct[cnt] = DCT(left(root), i); //作为一个析点
                child[cnt].push_back(root);
                st.pop();
                curr = cnt;
            }
        }
        st.push(curr);
        Seg.add(1, 1, i, -1); //因为r+1,所以max-min-(r-l)整体-1
    }
    dctRoot = root; //析合树的根也即是析点
}

int fa[N][T + 1];
int deep[N];

inline void dfs(const int curr, const int pa)
{
    deep[curr] = deep[pa] + 1;
    fa[curr][0] = pa;
    forn(i, 1, T)fa[curr][i] = fa[fa[curr][i - 1]][i - 1];
    for (const auto nxt : child[curr])dfs(nxt, curr);
}

inline int LCA(int x, int y)
{
    if (deep[x] < deep[y])swap(x, y);
    forv(i, T, 0)if (deep[fa[x][i]] >= deep[y])x = fa[x][i];
    if (x == y)return x;
    forv(i, T, 0)if (fa[x][i] != fa[y][i])x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}

//k级祖先
inline int kthRoot(int curr, int k)
{
    while (k)
    {
        const int step = ST.LOG2[k];
        curr = fa[curr][step];
        k -= 1 << step;
    }
    return curr;
}

int ansL, ansR;
//查找答案
inline void query(const int l, const int r)
{
    const int L = node[l], R = node[r];
    const int lca = LCA(L, R);
    //如果是lca是合点应该跳到合点下面一个点上的两个连续段依旧可以拼成连续段,析点自然是左右两边了
    if (type(lca))ansL = left(kthRoot(L,deep[L]-deep[lca]-1)), ansR = right(kthRoot(R,deep[R]-deep[lca]-1));
    else ansL = left(lca), ansR = right(lca);
    cout << ansL << " " << ansR << endl;
}

int q;

inline void solve()
{
    cin >> n;
    forn(i, 1, n)cin >> a[i];
    ST.build(); //建ST表
    build(); //建析合树
    dfs(dctRoot, 0);
    cin >> q;
    forn(i, 1, q)
    {
        int l, r;
        cin >> l >> r;
        query(l, r);
    }
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

\[时间复杂度：建树\ O(n\log{n})，查询\ O(m\log{n})
\]