卡特兰数-Catalan数

卡特兰数的含义：

说到卡特兰数，就不得不提及卡特兰数序列。卡特兰数序列是一个整数序列。其通项公式是我们从中取出的就叫做第n个卡特兰数数，前几个卡特兰数数是：1,
1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, …运用卡特兰数能够解决很多实际问题上的计数问题

卡特兰数的几个基本性质以及变形公式：（提示括号一上n一下m表示n中选择m个的组合数）

1、-->>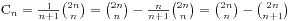

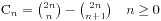
2、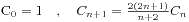

3、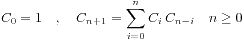

4、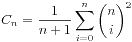

以上的推导公式为其基本性质总结，假设有计数问题可以装换为以上几个公式那么他们就是卡特兰数的变形

直接运用卡特兰数的公式：f(n+1)=(4*n-6)/n*f(n)进行计算。

卡特兰数变形运用：

n个+1和n个-1构成2n项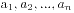。其部分和满足的序列个数等于卡特兰数。

证明：

我们如果不满足条件的序列个数为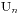，那么就有。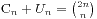

接着就是求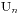了，我们如果有一个最小的k令。

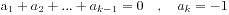因为这里k是最小的(注k为最小的令的值，所以在K之前肯定是>=0的)，所以必有，而且k是一个奇数不是偶数。此时我们仅仅将前k项中的+1变为-1。将-1变为+1,那么对于0-2*n。就能得到一个有(n+1)个+1和(n-1)个-1的序列了。如此。从2*n中提取出n+1个+1或者n-1个-1,便是我们所求的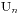，数值大小为 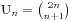。那么我们就得到了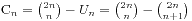就是我们基本性质中的第一个。

变形：

1.将-1看成右括号。+1看成左括号，就变成了合法括号表达式的个数。

2.n+1个数连乘。乘法顺序有种

3.n个节点的二叉树的全部可能形态数为

我们考虑随便取一个节点作为根，那么他左边和右边的儿子节点个数就确定了。假定根节点标号为x，那么左子树的标号就从1到x-1,共x-1个，右子树的标号就从x+1到n。共n-x个，那么我们的x从1取到n，就获得了全部的情况数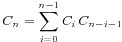就是我们基本性质中的第三个

4.对于一个n*n(记住是n*n，当然，假设你使用n*m也可。可是须要改变公式)的正方形网格，每次我们能向右或者向上移动一格，那么从左下角到右上角的全部在副对角线右下方的路径总数为。

我们将一条水平边记为+1,垂直边记为-1,那么就组成了一个n个+1和n个-1的序列。我们所要保证的就是前k步中水平边的个数不小于垂直边的个数。换句话说前k个元素的和非负即，就是我们证明的第一个。

5.凸n+2边形进行三角形切割（仅仅连接顶点对形成n个三角形）数：下面是n=4的情况

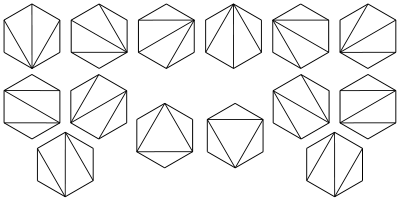
6.n个数入栈后的出栈的排列总数是。比如1,2,3入栈的出栈排序有123，132，213，231和321五种

7.对于集合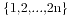的不交叉划分的数目为,不交叉划分即两个区间能够包括或者相离，可是不能够交叉，就像两个圆之间的关系一样。能够圆包括圆。相离。可是不能相交

8.n层的阶梯分割为n个矩形的切法数也是。例如以下图所看到的：（下面为n=4的情况）

证明暂无

9.在一个2*n的格子中填入1到2n这些数值使得每一个格子内的数值都比其右边和上边的全部数值都小的情况数也是。

10.平面上连接能够形成凸包的2n个点分成2个一组连成n条线段。两两线段之间不相交的情况总数是，