7-ZIP可以打开,右击提取到当前目录即可

 

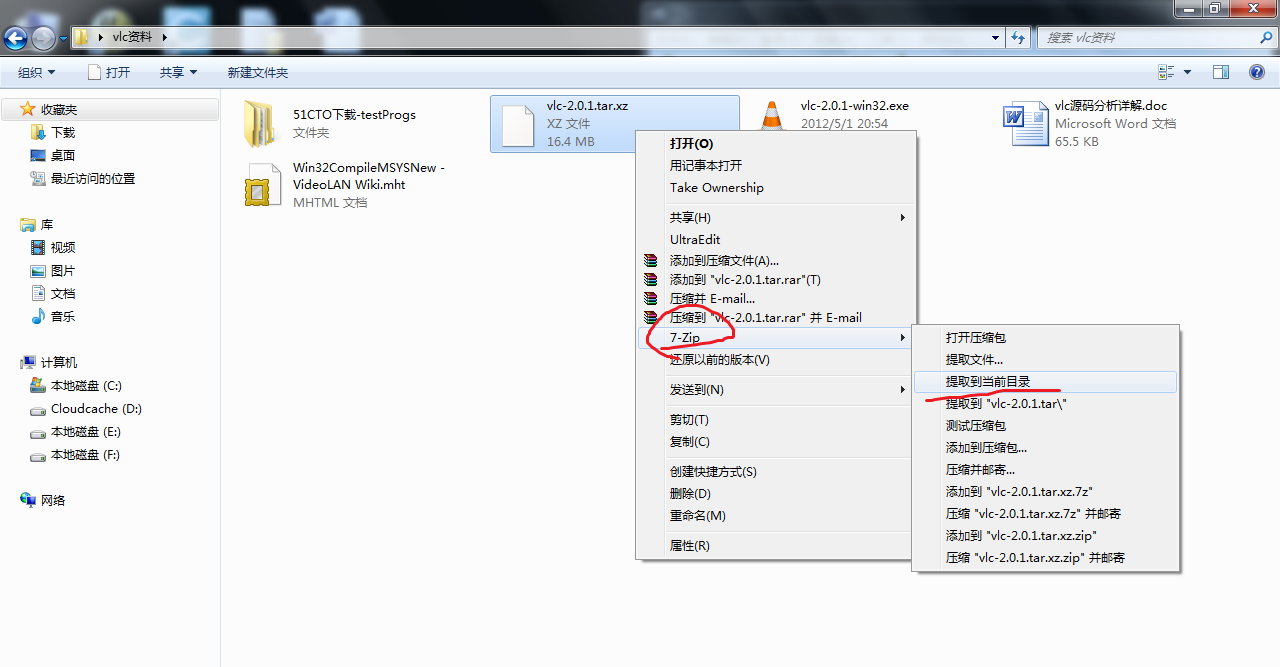
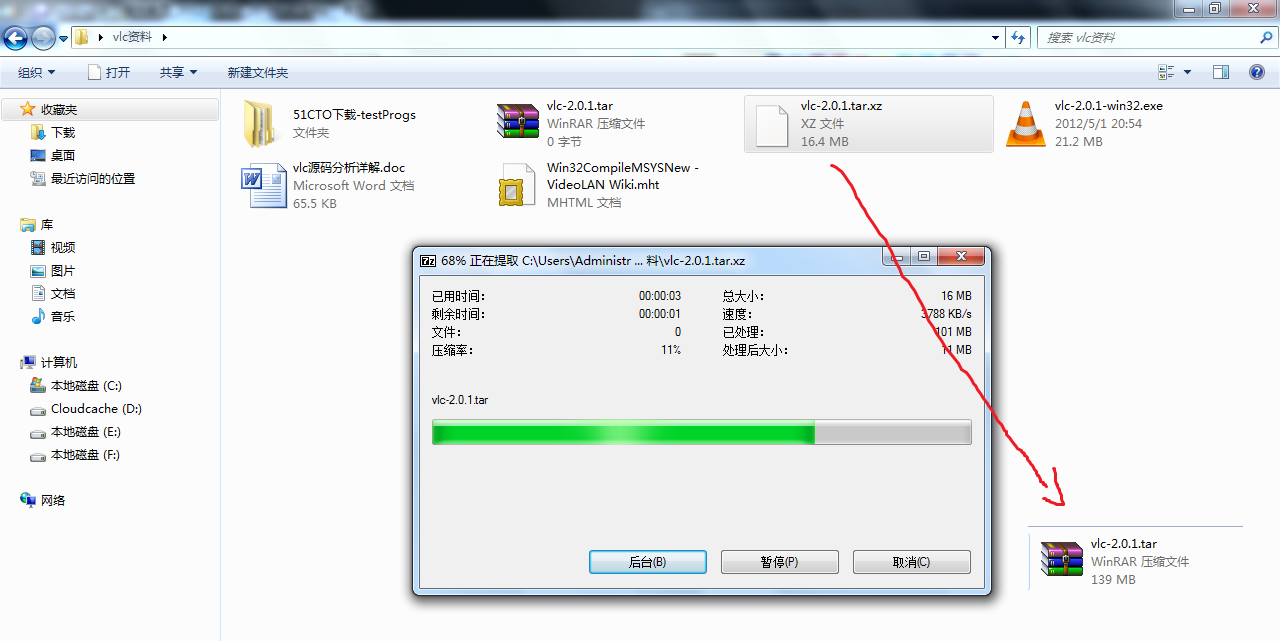
发现这个压缩比例还是相当不一般的,都快十倍了.

百科知识 .tar.xz文件如何打开的更多相关文章

  1. 百科知识 .e,.ec文件如何打开

    1 .e是易语言源文件,你可以从以下网址下载e语言编程环境: http://www.xiazaiba.com/html/409.html   2 安装之后会自动关联.e文件.   3 打开一个e语言文 ...

  2. (转)tar.xz文件如何解压

    XZ压缩最新压缩率之王 xz这个压缩可能很多都很陌生,不过您可知道xz是绝大数Linux默认就带的一个压缩工具. 之前xz使用一直很少,所以几乎没有什么提起. 我是在下载phpmyadmin的时候看到 ...

  3. tar.xz文件解压

    原文:http://blog.csdn.net/rheostat/article/details/7614451 感谢CSDN的<帝都码农> ======================= ...

  4. tar.xz文件如何解压

    1. tar.xz介绍 XZ压缩最新压缩率之王 xz这个压缩可能很多都很陌生,不过您可知道xz是绝大数linux默认就带的一个压缩工具. 之前xz使用一直很少,所以几乎没有什么提起. 2. 压缩 ta ...

  5. tar.xz文件如何解压 (已验证）

    XZ压缩最新压缩率之王 xz这个压缩可能很多都很陌生,不过您可知道xz是绝大数linux默认就带的一个压缩工具. 之前xz使用一直很少,所以几乎没有什么提起. 我是在下载phpmyadmin的时候看到 ...

  6. linux下tar.xz 文件解压

    在linux下下载源码文件安装时有些会遇到tar.xz文件的解压,习惯了tar解压缩,第一次遇到.xz文件还是有点迷惑,google 如下,解压这种格式的文件需要xz工具,如果xz工具没有安装,则安装 ...

  7. tar.xz 文件如何解压

    XZ压缩最新压缩率之王 xz这个压缩可能很多都很陌生,不过您可知道xz是绝大数linux默认就带的一个压缩工具. 之前xz使用一直很少,所以几乎没有什么提起. 我是在下载phpmyadmin的时候看到 ...

  8. tar.xz文件怎样解压

    XZ压缩最新压缩率之王 xz这个压缩可能非常多都非常陌生,只是您可知道xz是绝大数linux默认就带的一个压缩工具. 之前xz使用一直非常少,所以差点儿没有什么提起. 我是在下载phpmyadmin的 ...

  9. .tar.xz文件的解压方法

    废话不多说: 直接看 方法一: tar -xvJf ***.tar.gz 方法二: 先减压成 .tar 格式的文件, 再解压 .tar #xz是一个工具, 系统中没有安装,需要下载 xz -d *** ...

随机推荐

  1. 记一次运行spark程序遇到的权限问题

    设置回滚点在本地运行时正常,在集群时就报错,后来是发现ceshi这个目录其他用户没有写的权限,修改其他用户的权限就好了 hdfs dfs - /ceshi

  2. Python全栈开发第二期课表

     day01-python 全栈开发-基础篇                 01 开课介绍 01:55:13 ★  02 开课介绍02 01:28:31 ★  03 开课介绍03 00:22:55 ...

  3. 面试问题整理Andorid版本 date: 2017-1-12 21:14:36 categories: 技术

    Acitivty的四中启动模式与特点. standard:默认的启动模式 singleTop:适合那种接受通知启动的页面,比如新闻客户端之类的,可能会给你推送好几次 ,但是每次都是打开同一张页面调用o ...

  4. BZOJ 4819 [Sdoi2017]新生舞会 ——费用流 01分数规划

    比值最大 分数规划 二分答案之后用费用流进行验证. 据说标称强行乘以1e7换成了整数的二分. 不过貌似实数二分也可以过. #include <map> #include <cmath ...

  5. Qtree

    Qtree Ⅰ 题意:https://vjudge.net/problem/SPOJ-QTREE 带修路径查询最大边权 sol :树链剖分,之后每条重链就是一个连续的区间,拿线段树维护即可  简单讲讲 ...

  6. linux--bash: redis-server: 未找到命令

    linux 安装redis过程中出现了异常,make不通过,异常如下: [root@localhost redis-2.8.3]# make cd src && make all ma ...

  7. Android ARM指令学习

    在逆向分析Android APK的时候,往往需要分析它的.so文件.这个.so文件就是Linux的动态链接库,只不过是在ARM-cpu下编译的.所以学习Android下的ARM指令很重要.目前,市面上 ...

  8. 使用Collectors.toMap遇到NullPointerException

    这个坑也是踩过好几次了,记录一笔. 当试图使用Collectors.toMap将一个stream收集为Map的时候,若构造map的valueMapper返回null时,则会报NullPointerEx ...

  9. hdu 4870 rating(高斯消元求期望)

    Rating Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)Total Sub ...

  10. LA 6450 social advertising(dfs剪枝)

    6450 Social AdvertisingYou have decided to start up a new social networking company. Other existing ...