MIP启发式算法：local branching

*本文主要是记录并分享最近学习到的知识，算不上原创

*参考文献见链接

本文主要是讲述local branching算法，主要以M. Fischetti的论文 “Local braching”和Pierre Hansen的论文“Variable neighborhood search and local branching”为参考文献。

https://link.springer.com/article/10.1007/s10107-003-0395-5

https://www.sciencedirect.com/science/article/pii/S0305054805000894

引言

local branching可以说的上集合了启发式算法和精确算法的特质，读者既可以从local search的角度去理解它，也可以从branch and bound的角度去认识它。

接下来，我会从local search的角度去认识local branching，也建议读者先用local search的思想去认识它。

local branching 以local search为核心框架，它的特色在于定义邻域结构的方式：借用variable fixing heuristic的思想，利用hamming distance概念构造不等式，从而确定了邻域。这些不等式可以被称为local branching cuts。local branching 的优点在于可以在求解早期就获得不错的解。

Hamming distance

首先，我们说一下hamming distance。

hamming distance是一种关于距离的定义。我们自然可以想到这种距离的定义不是唯一的，我们可以用其他的合适的距离公式来定义邻域结构。hamming distance用来判断两个字符串的差异（“距离”），指的是两个字符串中对应字符不相同的数目。

例如：

s1：1 0 1 0

s2：1 1 0 0

hamming distance为2。

所以说，如果当前解如s1, 我们将邻域结构定义为“hamming distance ≤1”，那么邻域就是{{0 0 1 0}, {1 1 1 0},{1 0 0 0}, {1 0 1 1}}。

对于0-1规划问题而言，由于变量只能取值0或1，所以用hamming distance来刻画两个解的“距离”，是很合适的，但是，对于一般的整数规划问题或者混合整数规划问题，用hamming distance来刻画两个解的“距离”，会有些不太贴切，做些调整是有必要的。所以，个人认为，利用hamming distance来构造不等式的local branching更适合于0-1规划问题，或者说大部分变量都是0-1变量的问题。

local branching 的过程

local braching 的特殊之处就在于定义邻域结构的方式，所以我们首先弄清楚local braching是如何定义邻域的。

定义邻域结构

basic local braching的过程

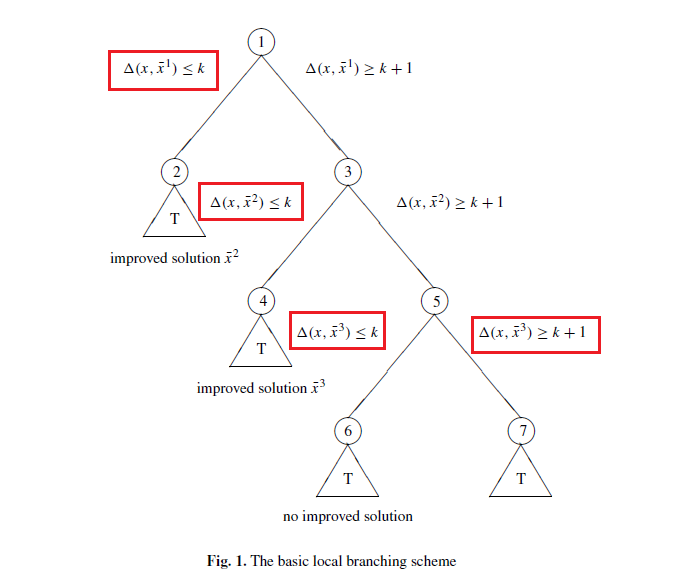
（1）生成初始解：生成初始解，比如通过Cplex求解获得初始解；

（2）定义邻域和候选解：将local braching cuts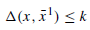加到原问题中，调用Cplex求解新问题的最优解，求解后恢复成原问题（删掉刚加的local branching cuts）；

（3）确定新解：如果Cplex求得的新问题的最优解优于当前解，就用最优解替代当前解，作为新解，并且将加入到原问题中，避免重复搜索；

（4）迭代：重复上述搜索过程，直到Cplex求得的新问题的最优解劣于当前解。此时，加入，调用Cplex求取最优解。

general local braching的过程

general local braching 相较于basic local braching，考虑到了：

（1）Time limit on left-branch nodes

（2）Diversification

general local braching的伪代码（local branching + Cplex）

参考文献

Fischetti, M. and Lodi, A., 2003. Local branching. Mathematical programming, 98(1-3), pp.23-47.

Hansen, P., Mladenović, N. and Urošević, D., 2006. Variable neighborhood search and local branching. Computers & Operations Research, 33(10), pp.3034-3045.