POJ1523(割点所确定的连用分量数目,tarjan算法原理理解)

SPF

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7406		Accepted: 3363

Description

Consider the two networks shown below. Assuming that data moves around these networks only between directly connected nodes on a peer-to-peer basis, a failure of a single node, 3, in the network on the left would prevent some of the still available nodes from communicating with each other. Nodes 1 and 2 could still communicate with each other as could nodes 4 and 5, but communication between any other pairs of nodes would no longer be possible.

Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.

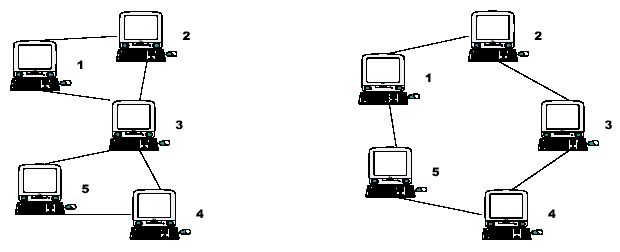
Input

The input will contain the description of several networks. A network description will consist of pairs of integers, one pair per line, that identify connected nodes. Ordering of the pairs is irrelevant; 1 2 and 2 1 specify the same connection. All node numbers will range from 1 to 1000. A line containing a single zero ends the list of connected nodes. An empty network description flags the end of the input. Blank lines in the input file should be ignored.

Output

For each network in the input, you will output its number in the file, followed by a list of any SPF nodes that exist.

The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.

Sample Input

1 2
5 4
3 1
3 2
3 4
3 5
0

1 2
2 3
3 4
4 5
5 1
0

1 2
2 3
3 4
4 6
6 3
2 5
5 1
0

0

Sample Output

Network #1
  SPF node 3 leaves 2 subnets

Network #2
  No SPF nodes

Network #3
  SPF node 2 leaves 2 subnets
  SPF node 3 leaves 2 subnets
题意:问将某个点删除可产生多少个连通分量。
思路：考察对tarjan算法原理理解，解释见代码。

#include"cstdio"
#include"cstring"
using namespace std;
const int MAXN=;
struct Edge{
    int to,next;
}es[MAXN*];
int V,E;
int head[MAXN];
inline int max(int u,int v)
{
    return u > v? u: v;
}
inline int min(int a,int b)
{
    return a > b? b: a;
}
void add_edge(int u,int v)
{
    es[E].to=v;
    es[E].next=head[u];
    head[u]=E++;
    V=max(max(u,v),V);
}
bool flag;
int root;
int subnets[MAXN];
int index;
int dfn[MAXN],low[MAXN];
void tarjan(int u,int fa)
{
    int son=;
    dfn[u]=low[u]=++index;
    for(int i=head[u];i!=-;i=es[i].next)
    {
        int v=es[i].to;
        if(!dfn[v])
        {
            tarjan(v,u);
            son++;
            low[u]=min(low[u],low[v]);
            if((u==root&&son>)||(u!=root&&dfn[u]<=low[v]))
            {
                flag=true;
                subnets[u]++;
                //u->v  该边导致u成为割点
                //当dfn[u]==low[v]时u->v为返祖边,u、v处于同一双连通分量中
                //当dfn[u]<low[v]时u->v为割边
                //删除割点u产生的连通数目为:u所在的连通分量数目+与u所连接的割边的数目+1(边:fa->u)
            }
        }
        else if(v!=fa) low[u]=min(low[u],dfn[v]);
    }
}
int main()
{
    int cas=;
    int u,v;
    while(true)
    {
        v=-;
        index=;
        memset(subnets,,sizeof(subnets));
        memset(dfn,,sizeof(dfn));
        memset(low,,sizeof(low));
        memset(head,-,sizeof(head));
        V=-,E=;
        flag=false;
        while(scanf("%d",&u)&&u)
        {
            scanf("%d",&v);
            add_edge(u,v);
            add_edge(v,u);
        }
        if(v==-)    break;
        root=V;
        tarjan(root,-);
        printf("Network #%d\n",++cas);
        if(flag)
        {
            for(int i=;i<=V;i++)
            {
                if(subnets[i]>)
                {
                    printf("  SPF node %d leaves %d subnets\n",i,subnets[i]+);//加上fa->u该边所连接的连通分量
                }
            }
        }
        else    printf("  No SPF nodes\n");
        printf("\n");
    }
    return ;
}