【NOIP2016】愤怒的小鸟搜索

题目描述

Kiana 最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 (0,0)(0,0) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 y=ax^2+bxy=ax2+bx 的曲线，其中 a,ba,b 是Kiana 指定的参数，且必须满足 a < 0a<0，a,ba,b 都是实数。

当小鸟落回地面（即 xx 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 nn 只绿色的小猪，其中第 ii 只小猪所在的坐标为 \left(x_i,y_i \right)(xi,yi)。

如果某只小鸟的飞行轨迹经过了 \left( x_i, y_i \right)(xi,yi)，那么第 ii 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过 \left( x_i, y_i \right)(xi,yi)，那么这只小鸟飞行的全过程就不会对第 ii 只小猪产生任何影响。

例如，若两只小猪分别位于 (1,3)(1,3) 和 (3,3)(3,3)，Kiana 可以选择发射一只飞行轨迹为 y=-x^2+4xy=−x2+4x 的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有 TT 个关卡，现在 Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入输出格式

输入格式：

第一行包含一个正整数 T，表示游戏的关卡总数。

下面依次输入这 T 个关卡的信息。每个关卡第一行包含两个非负整数 n,m n,m，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 n行中，第 i行包含两个正实数 xi,yi，表示第 i 只小猪坐标为 (xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 m=0，表示Kiana输入了一个没有任何作用的指令。

如果 m=1，则这个关卡将会满足：至多用 ⌈n/3+1⌉ 只小鸟即可消灭所有小猪。

如果 m=2，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少 ⌊n/3⌋ 只小猪。

保证 1≤n≤18，0≤m≤2，0<xi,yi<10，输入中的实数均保留到小数点后两位。

上文中，符号⌈c⌉ 和 ⌊c⌋ 分别表示对 c 向上取整和向下取整，例如：\lceil 2.1 \rceil = \lceil 2.9 \rceil = \lceil 3.0 \rceil = \lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。

输出格式：

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

输入输出样例

输入样例#1：

输出样例#1：

1

1

输入样例#2：

输出样例#2：

输入样例#3：

输出样例#3:

说明

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同，22只小猪分别位于(1.00,3.00)(1.00,3.00)和 (3.00,3.00)(3.00,3.00)，只需发射一只飞行轨迹为y = -x^2 + 4xy=−x2+4x的小鸟即可消灭它们。

第二个关卡中有55只小猪，但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6xy=−x2+6x上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

------------------------------------------------------------------

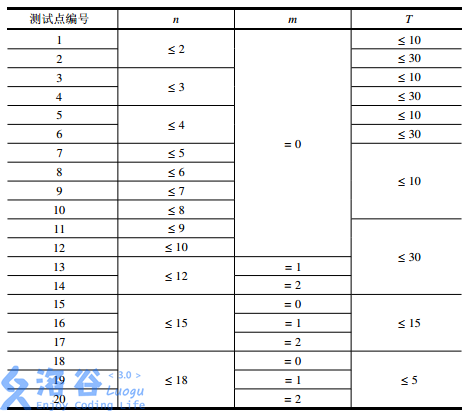
听说这道题要用状压.....但基于现在我能避开DP就尽量避开Dp的策略我选择爆搜一波（悄悄撒花

其实搜并没有什么思维难度甚至用不上题目给的m的信息

对于每只猪了，存在两种情况：

1.和之前的某猪连成线我们可以暴力枚举算出抛物线的系数用na[i]和nb[i]记录

2.不和之前的某猪连成线那么就加入单独成线的行列之中用 dx[i]和dy[i]记录

每次dfs传入三个信息(now,u,v)// now当前猪 u被安排过了 v各自成一条线

P.S. :当时以为找之前的猪和从单个猪的行列中取出一只猪暴力会GG 结果居然就这么水过去了？？？？

MARK：

1.请注意哪些数组需要开为double

2.判断两个浮点数相同的方式：做差之后小于某精度

double eps=1e-8;

bool cmp(double a,double b)

{

　　return( fabs(a-b)<eps );

}

3.ans的剪枝和更新条件、方式

以下代码

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #include<cmath>

 #define N 50

 using namespace std;

 struct node

 {

     double x,y;

 }e[N];

 int n,m,ans;

 double na[N],nb[N];

 double dx[N],dy[N];

 double eps=1e-;

 bool cmp(double a,double b)

 {

     return( fabs(a-b)<eps );

 }

 void dfs(int now,int u,int v)//now当前猪 u被安排 v各自一条线

 {

     if(u+v>=ans) return;

     if(now>n)

     {

         ans=u+v;

         return;

     }

     bool flag=;

     for(int i=;i<=u;i++)

         if( cmp(e[now].x*e[now].x*na[i]+e[now].x*nb[i],e[now].y) )//之前在线上

         {

             dfs(now+,u,v);

             flag=;

             break;

         }

     if(!flag)

     {

         for(int i=;i<=v;i++)//选择和之前的猪连成一线

         {

             if( cmp(e[now].x,dx[i]) ) continue;

             double a=(dx[i]*e[now].y-e[now].x*dy[i])/(e[now].x*e[now].x*dx[i]-e[now].x*dx[i]*dx[i]);

             double b=(e[now].y-a*e[now].x*e[now].x)/(e[now].x);

             if(a<)

             {

                 na[u+]=a; nb[u+]=b;//记下这条线

                 double piu=dx[i],biu=dy[i];

                 for(int j=i;j<=v;j++)//暴力哭了的减单

                 {

                      dx[j]=dx[j+];

                      dy[j]=dy[j+];

                 }

                 dfs(now+,u+,v-);

                 for(int j=v;j>=i;j--)//暴力哭了的加单

                 {

                      dx[j]=dx[j-];

                      dy[j]=dy[j-];

                 }

                 dx[i]=piu; dy[i]=biu;

             }

         }

         //选择不和现在的猪构成一个新线

         dx[v+]=e[now].x;

         dy[v+]=e[now].y;

         dfs(now+,u,v+);

     }

 }

 int main()

 {

     int t;

     scanf("%d",&t);

     while(t--)

     {

         scanf("%d%d",&n,&m);

         for(int i=;i<=n;i++)

             scanf("%lf%lf",&e[i].x,&e[i].y);

         ans=;

         dfs(,,);

         printf("%d\n",ans);

     }

     return ;

 }

 /*

 1

 5 2

 1.00 5.00

 2.00 8.00

 3.00 9.00

 4.00 8.00

 5.00 5.00

 */