hihoCoder [Offer收割]编程练习赛83 D 生成树问题

题目

从 Kruskal 算法的角度来思考这个问题。

考虑 $n$ 个点的“空图”（即没有边的图）。
先将 $m_2$ 条无权值的边加到图中，得到一个森林。

按边权从小到大的顺序枚举 $m_1$ 条有权值的边。
对于边 $e\colon(u, v, w)$，若将 $e$ 加入图中之后

(i) 会形成环，这意味着 $u$ 到 $v$ 的路径上的所有边的权值都不大于 $w$；

(ii) 不会形成环，则将其加入图中。

我们需要解决的问题：$m_2$ 条原本无权值的边在形如“$u$ 到 $v$ 的路径上的所有边的权值都不大于 $w$”的约束之下，每条边的最大权值是多少。

可以用树链剖分来帮助计算。
复杂度 $O(n\log^2n)$

正确性

首先，容易证明上述算法为每条原本无权值的边所确定的权值能够使得这些边出现在某个最小生成树中（充分性）。
其次，假设上述算法为某条原本无权值的边 $(u,v)$ 所确定的权值为 $w$，若将边 $(u,v)$ 的权值改为 $w+1$，则这条边必然不存在于任意一棵生成树中（必要性）

猜想
其实对 $m_1$ 条边按权值排序是不必要的，按什么顺序枚举这 $m_1$ 条边对结果并无影响。

这猜想是错的。

反列

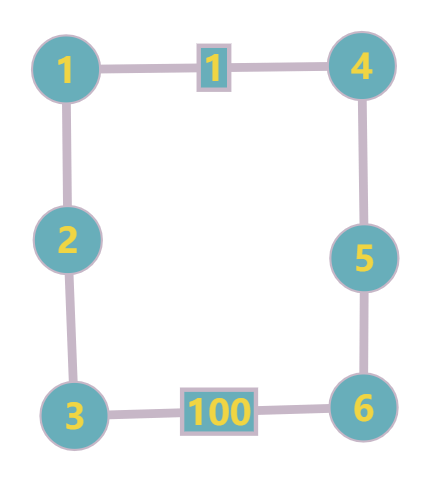
Implementation

https://gist.github.com/GoBigorGoHome/6787ee01dbf1a2ba411d8baeea75e4a2

---

（以下内容有误）

另一种解法

我们不必把最小生成树真实的形态存下来。
按照上面的分析，我们只要知道在我们构造的那棵最小生成树中任意两点间的路径上有哪些边就可以了。

形式化地说，考虑两棵树 $T$，$T'$，它们的边集分别为 $E$，$E'$，我们要构造一个 $E$ 到 $E'$ 的双射，使得在这两棵树中，任意两点 $u,v$ 之间的路径的边集都相等，即 $\forall u, v$，$E(u,v) = E'(u,v)$

我们发现在 Kruskal 算法中，并查集合并子树时，如果按秩合并且不采用路径压缩，那么最后得到的树就符合上述要求。

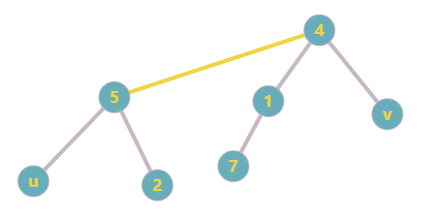
以上图为例，将设我们要往图中加入边 $(u,v)$，那么我们可以把边 $(4,5)$ 当作边 $(u,v)$，可以证明在并查集对应的树中点 $a$ 到点 $b$ 需要经过边 $(4,5)$ 当且仅当在原生成树中从点 $a$ 到点 $b$ 需要经过边 $(u,v)$ 。