Codeforces 906D Power Tower（欧拉函数 + 欧拉公式）

题目链接  Power Tower

题意  给定一个序列，每次给定$l, r$

　　 求$w_{l}^{w_{l+1}^{w_{l+2}^{...^{w_{r}}}}}$  对m取模的值

根据这个公式

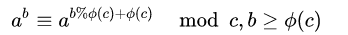
每次递归计算。

因为欧拉函数不断迭代，下降到$1$的级别大概是$log(m)$的，那么对于每一次询问最多需要递归$log(m)$次

注意每次求解欧拉函数的时候要用map存下来，方便以后查询

#include <bits/stdc++.h>

using namespace std;

#define rep(i, a, b)	for (int i(a); i <= (b); ++i)
#define dec(i, a, b)	for (int i(a); i >= (b); --i)

typedef long long LL;

const int N = 1e5 + 10;

int n, q;
LL a[N];
LL m;
map <LL, LL> f;

LL phi(LL n){
	if (f.count(n)) return f[n];
	LL ans = n, z = n;
	for (LL i = 2; i * i <= n; ++i){
		if (n % i == 0){
			ans -= ans / i;
			while (n % i == 0) n /= i;
		}
	}

	if (n > 1) ans -= ans / n;
	return f[z] = ans;
}

LL Pow(LL a, LL b, LL mod){
	LL ret = 1;
	LL fl  = a >= mod;
	for (; b; b >>= 1){
		if (b & 1){
			ret *= a;
			if (ret >= mod) fl = 1, ret %= mod;
		}

		a *= a;
		if (a >= mod) a %= mod, fl = 1;
	}

	return ret + fl * mod;
}

LL solve(int l, int r, LL mod){
	if (l == r) return a[l];
	if (mod == 1) return 1;
	return Pow(a[l], solve(l + 1, r, phi(mod)), mod);
}

int main(){

	scanf("%d%lld", &n, &m);
	rep(i, 1, n) scanf("%lld", a + i);

	scanf("%d", &q);
	while (q--){
		int x, y;
		scanf("%d%d", &x, &y);
		printf("%lld\n", solve(x, y, m) % m);
	}

	return 0;
}