●BZOJ 4289 PA2012 Tax

●赘述题目

算了，题目没有重复的必要。

注意理解：对答案造成贡献的是每个点，就是了。

举个栗子：

对于如下数据：

2 1

1 2 1

答案是 2；

●题解

方法：建图(难点)+最短路。

先来几个链接：（他们为我解题提供了思路，但有些部分看得我有点mengbi）

●http://blog.csdn.net/pure_w/article/details/55060079

●http://www.cnblogs.com/clrs97/p/5046933.html

●建图：

1.把原图的双向边拆成两条单向边（权值不变）。并把每条单向边看成一个点（称为新图点）；

2.建立源点S，S向1号点的出边（新图点）建单向边，权值为那些出边的权值。

3.建立汇点T，n号点的入边（新图点）向T建单向边，权值为那些入边的权值。

效果如下：

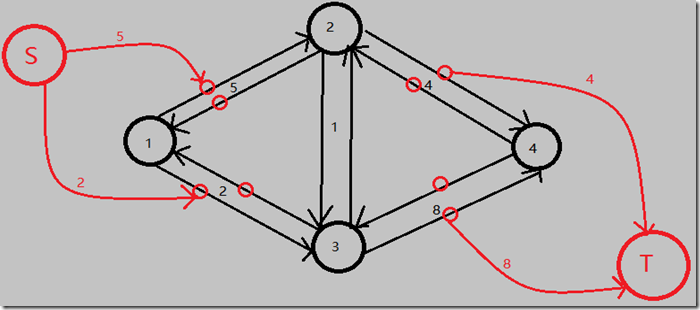
接下来是比较暴力的建边

(4.)枚举每个原图点X，把它的每条入边（新图点）向每条出边（新图点）建边，权值为这两条出入边的较大权值。（这样导致边巨多）

然后是比较优化的建边

4.（似乎叫差分边），枚举每个原图点X，先把它的出边（新图点）从小到大排序，排序后相邻的出边（新图点）间建两条有向边，小的指向大的边权为两者权值之差，大的指向小的边权为0。再枚举它的每个入边（新图点），向该原图点X的与该入边（新图点）权值相同的出边建边（为什么一定存在权值相同的入边和出边呢？因为我们把无向边变成了两个有向边），权值就为该相同权值。

（4.）和4.的建图效果如下：

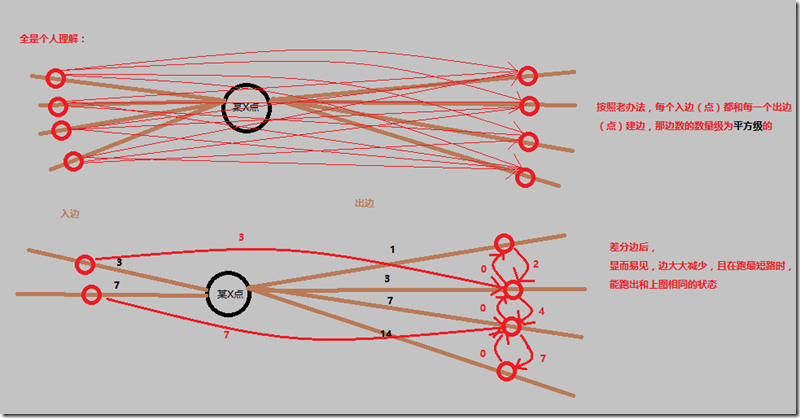
最后，新图已经建好，用4.建完图后，点和边的数量都可以接受，跑一个dijkstra就好啦！

●代码

#include<cstdio>
#include<cstring>
#include<queue>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
struct node{
	int p;long long d;
	bool operator <(const node &rtm) const {return d>rtm.d;}
};
struct edge{
	int to,co,next;
}e[400005*2],E[2000000];
int headin[100005],headout[100005],head[400010],nextout[400005*2],nextin[400005*2];
int st[200005];
int n,m,dnt=2,ent=1,S,T,cnt,p;
ll dis[400010];
bool vis[400010];
bool cmp(int x,int y) {return e[x].co<e[y].co;}
void add(int u,int v,int c){
	e[dnt]=(edge){v,c,0};  nextout[dnt]=headout[u];
	e[dnt]=(edge){v,c,0};  nextin[dnt]=headin[v];
	headout[u]=headin[v]=dnt++;

	e[dnt]=(edge){u,c,0};  nextout[dnt]=headout[v];
	e[dnt]=(edge){u,c,0};  nextin[dnt]=headin[u];
	headout[v]=headin[u]=dnt++;
}
void ADD(int u,int v,int c) {E[ent]=(edge){v,c,head[u]}; head[u]=ent++;}
void make_something(int x){
	cnt=0;
	for(int i=headout[x];i;i=nextout[i]) st[++cnt]=i;
	sort(st+1,st+cnt+1,cmp);
	for(int i=1;i<cnt;i++) ADD(st[i],st[i+1],e[st[i+1]].co-e[st[i]].co),ADD(st[i+1],st[i],0);
	for(int i=headin[x];i;i=nextin[i]) p=i^1,ADD(i,p,e[i].co);
}
void dijkstra(){
	node u; int v;
	memset(dis,0x7f,sizeof(dis));
	priority_queue <node> q;
	q.push((node){S,0}); dis[S]=0;
	while(!q.empty()){
		u=q.top(); q.pop();
		if(vis[u.p]) continue;  vis[u.p]=1;
		for(int i=head[u.p];i;i=E[i].next){
			v=E[i].to;
			if(!vis[v]&&dis[v]>dis[u.p]+E[i].co){
				dis[v]=dis[u.p]+E[i].co;
				q.push((node){v,dis[v]});
			}
		}
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1,a,b,c;i<=m;i++) scanf("%d%d%d",&a,&b,&c),add(a,b,c);
	// 建源点和汇点
	S=dnt++; T=dnt++;
	for(int i=headout[1];i;i=nextout[i]) ADD(S,i,e[i].co);
	for(int i=headin[n];i;i=nextin[i]) ADD(i,T,e[i].co);
	//枚举每一个原图点
	for(int i=1;i<=n;i++) make_something(i);
	dijkstra(); printf("%lld",dis[T]);
	return 0;
}