洛谷P2402 奶牛隐藏（网络流，二分答案，Floyd）

洛谷题目传送门

了解网络流和dinic算法请点这里（感谢SYCstudio）

题目

题目背景

这本是一个非常简单的问题，然而奶牛们由于下雨已经非常混乱，无法完成这一计算，于是这个任务就交给了你。(奶牛混乱的原因看题目描述)

题目描述

在一个农场里有n块田地。某天下午，有一群牛在田地里吃草，他们分散在农场的诸多田地上，农场由m条无向的路连接，每条路有不同的长度。

突然，天降大雨，奶牛们非常混乱，想要快点去躲雨。已知每个田地都建立有一个牛棚，但是每个牛棚只能容纳一定数量的牛躲雨，如果超过这个数量，那多出的牛只能去别的田地躲雨。奶牛们每移动1的距离花费1时间，奶牛们想知道它们全部都躲进牛棚，最少需要多少时间。(即最后一头奶牛最少要花多久才能躲进牛棚)。

输入输出格式

输入格式：

第一行输入两个整数N,M。N表示田地块数，M表示路径数。

接下来N行，每行两个整数S,P，分别表示该田地现在有几头牛以及该田地的牛棚最多可以容纳多少牛。

接下来M行，每行3个整数A,B,C，表示存在一条路径连接A,B，并且它的长度为C。

输出格式：

一个整数表示所有奶牛全都躲进牛棚所用的最少时间。如果无法使全部奶牛都躲进牛棚，输出-1。

输入输出样例

输入样例#1：

3 4

7 2

0 4

2 6

1 2 40

3 2 70

2 3 90

1 3 120

输出样例#1：

110

说明

样例解释

1号点的两只牛直接躲进1号牛棚，剩下的5只中，4只跑去2号点，还有一只从1->2->3,3号点的2只牛也直接躲进去，这样最慢的牛花费的时间是110。

数据范围

对于100%的数据，N<=200 M<=1500

思路分析

想到网络流不难。建一个超级源点连向每块田地，容量就是这块田里牛的数量。还要建一个超级汇点，从每块田地连向它，容量就是棚子所能容纳的牛数量。只要满流了（即总流量等于总牛数），就说明当前解可行。

然而，对于田地之间的边又该如何处理呢？这里是最容易想偏的。。。。。。

其实我第一眼以为是取最后一次最大费用

跑最小费用最大流，每条田地之间的边费用就是它们的长度。这样貌似可以哈

然而很快就把这种诡异的办法给自己推翻掉了。

例子很简单。。。。。。

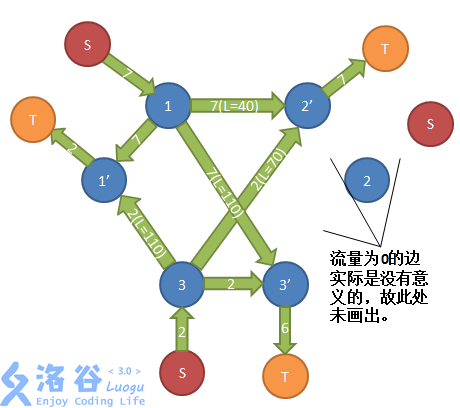
这张图的意思是，有3块田，1、2处各有一头牛，2、3处各有一个容量为1的棚。如果建费用流的图，就会长这个样子对吧。

试想一下跑费用流会发生什么。。。。。。

第一次，由S->2->T,没有费用；

第二次，由S->1->2->3->T,费用为2，跑完了。

然而，滑稽了。事实上，我们可以让两头牛一起动，1->2,2->3,最大的费用只有1。

因为费用流每次把最短的挑走了，使我们反而找不到答案。所以万万不能跑费用流了。

---

对于这种无法直接建模的题目，考虑二分答案。把每两点之间的最短距离用Floyd算出来，然后两两连边，边的容量均为INF。每次二分最长时间的取值，只把边长（即花费时间的长度）小于等于当前mid的边加进去，然后跑最大流。如果流满了就说明可行，把上界调至当前mid。否则把下界调至mid+1。一次次来，直到找到最终答案。

然而，数据范围超过了int，每次二分还要重新加边，再跑一遍dinic，时限可不能这么玩的！

于是，有必要来减少二分次数了。

既然点数是有限的，那么它们两两相连所产生的边数也不多，顶多几万条。而longlong取值范围太大了，即使二分，也需要跑五六十下（假如没卡INF大小的话），卡了以后也还是不小。

所以，可以把边按长度离散化，在边的集合上进行二分。把点两两之间的最短距离用floyd算出来以后，按长度sort一下，再按次序加入边集合中。还要按照长度的取值范围分成若干个小集合（即离散化）。因为已经有序了，所以直接在离散化后的序列上二分就好了。

加上一个比较方便的做法。把每个值在边集中的对应位置也记录下来。二分完，跑最大流最小割的时候，在这个位置之后的边（也就是边长比mid大的边，因为sort加离散化后较长的边加在了后面）都直接跳过。这样做又省去了重新建边的时间。

---

然后我就WA了，连样例都没过

调试了下发现，当我二分到70的时候，居然满流了。。。。。。

原来我没拆点，结果1<->2长度40的边和2<->3长度70的边连起来了。。。。。。

所以一定要拆点！！！边加两次就是了。

边的容量可以不用开到INF了，等于起点对应的牛数量就可以了（从那里只能跑出那么多牛嘛）。说不定可以优化常数

附上样例建图

吐槽一句TM这题目数据范围也没给清楚

所以还是要开longlong的，实测开intWA一个点。。。。。。

具体细节就看下面代码吧。加了不少优化，32s成功冲到当前本题rank1开了O2，欢迎超越。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
#define R register int
#define RL register LL
const int N=1009,M=200009;
const LL INF=1ll<<50;
struct EDGE{
    int a,b;
    LL l;
}e[M];//两点之间的连边存在这里排序
int S=0,T,SZ,he[N],ne[M],to[M],q[N],d[N],cur[N],grp[M];
LL LIM,f[M],mem[M],val[M],g[N][N];
#define G c=getchar()
#define in(z) G;\
    while(c<'-')G;\
    z=c&15;G;\
    while(c>'-')z*=10,z+=c&15,G;
#define min(x,y) x<y?x:y
#define min2(x,y) if(x>y)x=y
#define add(U,V,F)\
    to[++p]=V;ne[p]=he[U];he[U]=p;mem[p]=F;\
    to[++p]=U;ne[p]=he[V];he[V]=p;
inline bool cmp(EDGE x,EDGE y){return x.l<y.l;}
inline bool bfs()
{
    memset(d+1,0,SZ);
    for(R h=0,t=1;h<t;++h)
        for(R i=he[q[h]];i;i=ne[i])
            if(i<LIM&&f[i]&&!d[to[i]])
                d[q[t++]=to[i]]=d[q[h]]+1;
    return d[T];
}//i<LIM忽略编号超过限制的边
LL dfs(R u,RL mf)
{
    if(u==T)return mf;
    for(R&i=cur[u];i;i=ne[i])
        if(i<LIM&&f[i]&&d[to[i]]==d[u]+1)
        {
            RL cf=dfs(to[i],min(f[i],mf));
            if(cf){f[i]-=cf;f[i^1]+=cf;return cf;}
        }
    return 0;
}//以上是dinic模板
int main()
{
    R n,m,p=1,h=0,t=0,i,j,k,u,v;
    RL s,sum=0,res;
    register char c;
    in(n);in(m);T=n*2+1;SZ=(T+1)<<2;//S,T就是源汇点啦，SZ维护数组的长度
    for(i=1;i<=n;++i)
    {
        in(s);add(S,i,s);sum+=s;//统计一下牛的总数也就是总流量
        in(s);add(i+n,T,s);
    }
    for(i=1;i<=n;++i){add(i,i+n,mem[(i<<2)-2])};//mem之前存下了对应点的牛数
    for(i=1;i<=n;++i)
        for(j=1;j<i;++j)
            g[i][j]=INF;
    while(m--)
    {
        in(u);in(v);if(u<v){t=u;u=v;v=t;}
        in(s);min2(g[u][v],s);
    }
    for(k=1;k<=n;++k)
        for(i=1;i<=n;++i)
        {
            if(k==i)continue;
            s=k>i?g[k][i]:g[i][k];
            if(t==INF)continue;
            for(j=1;j<(min(k,i));++j)
                min2(g[i][j],s+g[k][j]);
            for(j=k+1;j<=i;++j)
                min2(g[i][j],s+g[j][k]);
        }//以上是Floyd，只用了半个矩阵，可能跑的快点吧
    for(i=1;i<=n;++i)
        for(j=1;j<i;++j)
            if(g[i][j]!=INF)
                e[h++]=(EDGE){i,j,g[i][j]};//加进去准备排序
    sort(e,e+h,cmp);
    s=0;
    for(i=0;i<h;++i)
    {
        if(s<e[i].l)//离散化，s放的是上一块的取值
        {			//值增加了，处理上一块
            grp[t]=p+1;//grp记下取值在边集数组中对应位置
            val[t++]=s;//val记下上一块的值
            s=e[i].l;//更新s
        }
        add(e[i].a,e[i].b+n,mem[(e[i].a<<2)-2]);
        add(e[i].b,e[i].a+n,mem[(e[i].b<<2)-2]);
    }
    grp[t]=p+1;val[t++]=s;
    grp[t]=p+3;val[t]=-1;//收下尾
    h=1;
    while(h!=t)//二分开始
    {
        LIM=grp[m=(h+t)>>1];//确定限制，dinic时忽略编号超过此限制的边
        memcpy(f,mem,(p+1)<<3);//每次把记好的边流量copy一下再跑
        res=0;
        while(bfs())
        {
            memcpy(cur,he,SZ);//加当前弧优化
            while((s=dfs(S,INF)))
                res+=s;
        }
        sum==res?t=m:h=m+1;
    }
    printf("%lld",val[h]);
    return 0;
}