源代码放在我的github上，想细致了解的可以访问：TriangleCount on github

一、实验要求

1.1 实验背景

        图的三角形计数问题是一个基本的图计算问题,是很多复杂网络分析(比如社交网络分析)的基础。目前图的三角形计数问题已经成为了 Spark 系统中 GraphX 图计算库所提供的一个算法级 API。本次实验任务就是要在 Hadoop 系统上实现图的三角形计数任务。

1.2 实验任务

        一个社交网络可以看做是一张图(离散数学中的图)。社交网络中的人对应于图的顶点;社交网络中的人际关系对应于图中的边。在本次实验任务中,我们只考虑一种关系——用户之间的关注关系。假设“王五”在 Twitter/微博中关注了“李四”,则在社交网络图中,有一条对应的从“王五”指向“李四”的有向边。图 1 中展示了一个简单的社交网络图,人之间的关注关系通过图中的有向边标识了出来。本次的实验任务就是在给定的社交网络图中,统计图中所有三角形的数量。在统计前,需要先进行有向边到无向边的转换,依据如下逻辑转换:

IF ( A→B) OR (B→A) THEN A-B
        “A→B”表示从顶点 A 到顶点 B 有一条有向边。A-B 表示顶点 A 和顶点 B 之间有一条无向边。一个示例见图 1,图 1 右侧的图就是左侧的图去除边方向后对应的无向图。
        **请在无向图上统计三角形的个数**。在图 1 的例子中,一共有 3 个三角形。
        本次实验将提供一个 [Twitter 局部关系图][1]作为输入数据(给出的图是有向图),请统计该图对应的无向图中的三角形个数。

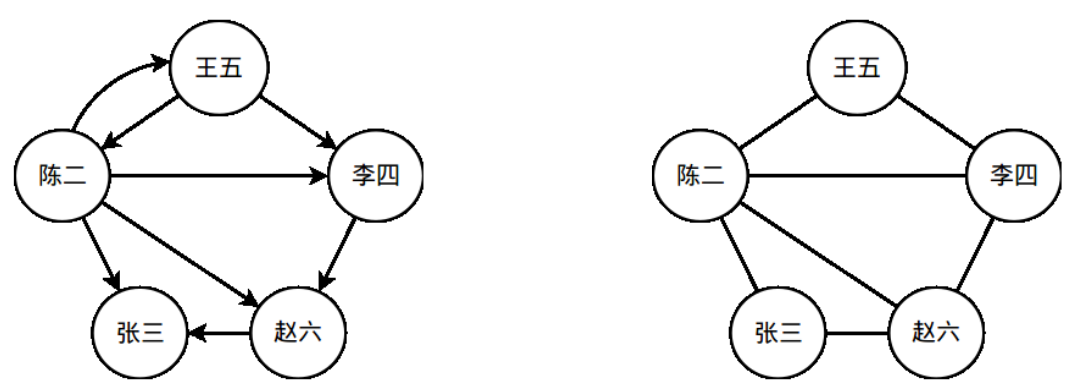
图 1 一个简单的社交网络示例。左侧的是一个社交网络图,右侧的图是将左侧图中的有向边转换为无向边后的无向图。

1.3 输入说明

        输入数据仅一个文件。该文件由若干行组成,每一行由两个以空格分隔的整数组成:

A B

A,B 分别是两个顶点的 ID。这一行记录表示图中具有一条由 A 到 B 的有向边。整个图的结构由该文件唯一确定。

下面的框中是文件部分内容的示例:

  1. 87982906 17975898
  2. 17809581 35664799
  3. 524620711 270231980
  4. 247583674 230498574
  5. 348281617 255810948
  6. 159294262 230766095
  7. 14927205 5380672

1.4 扩展

  • 扩展一：挑战更大的数据集!使用 Google+的社交关系网数据集作为输入数据集。

  • 扩展二：考虑将逻辑转换由or改为and的三角形个数是多少，改变后的逻辑转换如下：

IF ( A→B) AND (B→A) THEN A-B

二、实验设计与实现

2.1 算法设计

  • step1：统计图中每一个点的度，不关心是入度还是出度，然后对统计到的所有点的度进行排序
  • step2：将图中每一条单向边转换成双向边，对于图中a->b and b->a的两条边，分别转换后需要去重，在转换后的图中筛选出小度指向大度的边来建立邻接表，然后对每个点的邻接点按从小到大进行排序
  • step3：对原图中的边进行转换，确保每条边是由数值小的点指向数值大的点并去重，然后遍历每一条边：求边的两个端点对应的邻接点集的交集大小即为包含这条边的三角形个数。对每条边对应的三角形个数进行累加即可得到全图包含的三角形个数。

2.2 程序设计

  • 根据算法步骤将程序设计成4个job来实现：

    1. job:OutDegreeStat用于对每个点的度进行统计，在类OutDegreeStat中实现
    2. job:SortedOutDegree用于对所有点的度进行排序，在类OutDegreeStat中实现，在job1之后运行
    3. job:EdgeConvert用于建立存储小度指向大度的边的邻接表，在类EdgeConvert中实现
    4. job:GraphTriangleCount用于遍历每条边求端点对应邻接点集的交集来对三角形进行计数，在类GraphTriangleCount中实现

2.3 程序实现

  • job:OutDegreeStat的实现：

    1. Map阶段：(vertex1: Text, vertex2: Text) -> (vertex1: Text, 1: IntWritable) and (vertex2: Text, 1: IntWritable)，实现代码如下：

      1. public static class OutDegreeStatMapper extends Mapper<Object, Text, Text, IntWritable> {
      2.         private final IntWritable one = new IntWritable(1);
      4.         @Override
      5.         public void map(Object key, Text value, Context context)
      6.                 throws IOException, InterruptedException {
      7.             String line = value.toString();
      8.             StringTokenizer itr = new StringTokenizer(line);
      9.             Text vertex1 = new Text(itr.nextToken());
      10.             Text vertex2 = new Text(itr.nextToken());
      11.             if (!vertex1.equals(vertex2)) {
      12.                 context.write(vertex1, one);
      13.                 context.write(vertex2, one);
      14.             }
      15.         }
      16.     }

    2. Reduce阶段：(vertex: Text, degree: Iterable<IntWritable>) -> (vertex: Text, degreeSum: IntWritable)，实现代码如下：

      1. public static class OutDegreeStatReducer extends Reducer<Text, IntWritable, Text, IntWritable> {
      2.         @Override
      3.         public void reduce(Text key, Iterable<IntWritable> values, Context context)
      4.                 throws IOException, InterruptedException {
      5.             int sum = 0;
      6.             for (IntWritable val: values) {
      7.                 sum += val.get();
      8.             }
      9.             context.write(key, new IntWritable(sum));
      10.         }
      11.     }

    3. Combiner阶段：Combiner逻辑与Reduce逻辑一致，只是为了减少数据量从而减少通信开销

  • job:SortedOutDegree的实现：

    1. Map阶段：由于mapreduce的reduce阶段会按key进行排序，为了按度进行排序，只需用hadoop自带的InverseMapper类对键值对做逆映射(vertex: Text, degree: IntWritable) -> (degree: IntWritable, vertex: Text)即可。
    2. Reduce阶段：无需设置Reducer类，hadoop的Reduce阶段自动会对degree进行排序

  • job:EdgeConvert的实现：

    1. Map阶段：(vertex1: Text, vertex2: Text) -> (vertex1: Text, vertex2: Text) and (vertex2: Text, vertex1: Text)，实现代码如下：

      1.  public static class EdgeConvertMapper extends Mapper<Object, Text, Text, Text> {
      2.         @Override
      3.         public void map(Object key, Text value, Context context)
      4.                 throws IOException, InterruptedException {
      5.             StringTokenizer itr = new StringTokenizer(value.toString());
      6.             Text vertex1 = new Text(itr.nextToken());
      7.             Text vertex2 = new Text(itr.nextToken());
      8.             if (!vertex1.equals(vertex2)) {
      9.                 context.write(vertex1, vertex2);
      10.                 context.write(vertex2, vertex1);
      11.             }
      12.         }
      13.     }

    2. Reduce阶段：在setup函数中读取存储节点度的文件，在reduce函数中(vertex1: Text, vertex2List: iterable<Text>) -> (vertex1 with minimal degree: Text, vertex2 with maximal degree: Text)，在对邻接表节点进行排序时，要重写一个String Comparator，让String按它所表示的数值大小进行比较，实现代码如下：

      1. public static class EdgeConvertReducer extends Reducer<Text, Text, Text, Text> {
      2.         private Map<String, Integer> degree;
      3.         private Map<String, Boolean> edgeExisted;
      4.         private URI[] cacheFiles;
      6.         @Override
      7.         public void setup(Context context)
      8.                 throws IOException, InterruptedException {
      9.             degree = new HashMap<String, Integer>();
      11.             //读取存储节点度的文件
      12.             Configuration conf = context.getConfiguration();
      13.             cacheFiles = context.getCacheFiles();
      14.             for (int i = 0; i < cacheFiles.length; i++) {
      15.                 SequenceFile.Reader reader = new SequenceFile.Reader(conf, SequenceFile.Reader.file(new Path(cacheFiles[i])));
      16.                 IntWritable key = new IntWritable();
      17.                 Text value = new Text();
      18.                 int cnt = 0;
      19.                 while (reader.next(key, value)) {
      20.                     degree.put(value.toString(), cnt);
      21.                     cnt++;
      22.                 }
      23.                 reader.close();
      24.             }
      25.         }
      27.         @Override
      28.         public void reduce(Text key, Iterable<Text> values, Context context)
      29.                 throws IOException, InterruptedException{
      30.             Text vertex = new Text();
      31.             List<String> outvertex = new ArrayList<String>();
      32.             edgeExisted = new HashMap<String, Boolean>();  //记录已处理边以避免重复统计
      33.             for (Text val: values) {
      34.                 if (!edgeExisted.containsKey(val.toString())) {
      35.                     edgeExisted.put(val.toString(), true);
      36.                     //比较边两个端点的度大小
      37.                     if (degree.get(val.toString()) > degree.get(key.toString())) {
      38.                         outvertex.add(val.toString());
      39.                     }
      40.                 }
      41.             }
      42.             //对邻接节点从小到大进行排序，方便后续求交集
      43.             Collections.sort(outvertex, new ComparatorString());
      44.             for (String vt: outvertex) {
      45.                 vertex.set(vt);
      46.                 context.write(key, vertex);
      47.             }
      48.         }
      49.     }
      51.     //继承String比较器按它所表示的数值大小进行比较
      52.     public static class ComparatorString implements Comparator<String> {
      53.         public int compare(String a, String b) {
      54.             if (a.length() > b.length()) {
      55.                 return 1;
      56.             } else if (a.length() < b.length()){
      57.                 return -1;
      58.             } else {
      59.                 return a.compareTo(b);
      60.             }
      61.         }
      62.     }

  • job:GraphTriangleCount的实现：

    1. Map阶段：以job:EdgeConvert的输出文件作为读入，该文件不包含重复边因此无需判断转换，直接按原样映射(vertex1: Text, vertex2: Text) -> (vertex1: Text, vertex2: Text)即可，实现代码如下：

      1. public static class GraphTriangleCountMapper extends Mapper<Text, Text, Text, Text> {
      2.         @Override
      3.         public void map(Text key, Text value, Context context)
      4.                 throws IOException, InterruptedException{
      5.             context.write(key, value);
      6.         }
      7.     }

    2. Reduce阶段：在setup函数中读取存储小度指向大度的邻接表文件，在reduce函数中(vertex1: Text, vertex2List: Iterable<Text>) -> ("TriangleNum": Text, triangleNum: LongWritable)，在cleanup函数中写当前这个reducer的三角形计数结果，实现代码如下：

      1. public static class GraphTriangleCountReducer extends Reducer<Text, Text, Text, LongWritable> {
      2.         private final static String edgePath = TriangleCountDriver.HDFS_PATH + TriangleCountDriver.EdgeConvertPath;  //邻接表文件路径
      3.         private Map<String, Integer> vexIndex;  //存储节点的邻接表索引
      4.         private ArrayList<ArrayList<String>> vec = new ArrayList<ArrayList<String>>();  //存储全局邻接表
      5.         private long triangleNum = 0;
      7.         @Override
      8.         public void setup(Context context)
      9.                 throws IOException, InterruptedException {
      10.             int cnt = 0;
      11.             String lastVertex = "";
      12.             String sv, tv;
      13.             ArrayList<String> outVertices = new ArrayList<String>();
      14.             vexIndex = new TreeMap<String, Integer>();
      15.             //获取文件系统的接口
      16.             Configuration conf = context.getConfiguration();
      17.             FileSystem fs = FileSystem.get(conf);
      18.             //读取小度指向大度的边邻接表
      19.             for (FileStatus fst: fs.listStatus(new Path(edgePath))) {
      20.                 if (!fst.getPath().getName().startsWith("_")) {
      21.                     SequenceFile.Reader reader = new SequenceFile.Reader(conf, SequenceFile.Reader.file(fst.getPath()));
      22.                     Text key = new Text();
      23.                     Text value = new Text();
      24.                     while (reader.next(key, value)) {
      25.                         sv = key.toString();
      26.                         tv = value.toString();
      27.                         if (!sv.equals(lastVertex)) {
      28.                             if (cnt != 0) vec.add(outVertices);
      29.                             vexIndex.put(sv, cnt);
      30.                             cnt++;
      31.                             outVertices = new ArrayList<String>();
      32.                             outVertices.add(tv);
      33.                         } else {
      34.                             outVertices.add(tv);
      35.                         }
      36.                         lastVertex = sv;
      37.                     }
      38.                     reader.close();
      39.                 }
      40.             }
      41.             vec.add(outVertices);
      42.         }
      44.         @Override
      45.         public void reduce(Text key, Iterable<Text> values, Context context)
      46.                 throws IOException, InterruptedException{
      47.             for (Text val: values)
      48.                 if (vexIndex.containsKey(val.toString()))
      49.                     //调用求交集函数获取包含边(key,val)的三角形个数
      50.                     triangleNum += intersect(vec.get(vexIndex.get(key.toString())), vec.get(vexIndex.get(val.toString())));
      51.         }
      53.         @Override
      54.         public void cleanup(Context context) throws IOException, InterruptedException{
      55.             //将计数结果写入文件
      56.             context.write(new Text("TriangleNum"), new LongWritable(triangleNum));
      57.         }
      59.         //求有序集合的交集
      60.         private long intersect(ArrayList<String> avex, ArrayList<String> bvex) {
      61.             long num = 0;
      62.             int i = 0, j = 0;
      63.             int cv;
      64.             while (i != avex.size() && j != bvex.size()) {
      65.                 if (avex.get(i).length() > bvex.get(j).length()) {
      66.                     cv = 1;
      67.                 } else if (avex.get(i).length() < bvex.get(j).length()) {
      68.                     cv = -1;
      69.                 } else {
      70.                     cv = avex.get(i).compareTo(bvex.get(j));
      71.                 }
      72.                 if (cv == 0) {
      73.                     i++;
      74.                     j++;
      75.                     num++;
      76.                 } else if (cv > 0) {
      77.                     j++;
      78.                 } else {
      79.                     i++;
      80.                 }
      81.             }
      82.             return num;
      83.         }
      84.     }

2.4 扩展2的设计与实现

  • 对于a->b and b->a then a-b的条件，只需改变job:EdgeConvert的实现即可，新建一个job:UndirectionalEdgeConvert:

    1. Map阶段：以原数据文件作为输入进行映射转换：(vertex1: Text, vertex2: Text) -> ((vertex1, vertex2): Text, flag: Text) and ((vertex2, vertex1): Text, flag:Text)，按vertex1进行分区，其中flag作为节点序标记，用于帮助在Reducer中对双向边进行判断，如果输入的vertex1 > vertex2则flag置1，如果vertex1 < vertex2则flag置0，实现代码如下：

      1.  public static class UndirectionalEdgeConvertMapper extends Mapper<Object, Text, Text, Text> {
      2.         @Override
      3.         public void map(Object key, Text value, Context context)
      4.                 throws IOException, InterruptedException {
      5.             StringTokenizer itr = new StringTokenizer(value.toString());
      6.             String vertex1 = itr.nextToken();
      7.             String vertex2 = itr.nextToken();
      8.             String flag = "0";  //节点序标记，帮助Reducer判断双向边
      9.             if (!vertex1.equals(vertex2)) {
      10.                 if (vertex1.compareTo(vertex2) > 0) flag = "1";
      11.                 context.write(new Text(vertex1 + '\t' + vertex2), new Text(flag));
      12.                 context.write(new Text(vertex2 + '\t' + vertex1), new Text(flag));
      13.             }
      14.         }
      15.     }

    2. Reduce阶段：((vertex1, vertex2): Text, flagList: Iterable<Text>) -> (vertex1 with minimal degree: Text, vertex2 with maximal degree: Text)，如果flagList既包含0又包含1，则(vertex1, verex2)属于双向边，然后判断如果vertex2的度大于vertex1，则将vertex2加入到vertex1的邻接表中，reduce函数部分的实现代码如下：

      1. @Override
      2. public void reduce(Text key, Iterable<Text> values, Context context)
      3.     throws IOException, InterruptedException{
      4.     String[] term = key.toString().split("\t");
      5.     //如果邻接表出点变了则写出lastkey为出点的邻接表
      6.     if (!lastKey.equals(term[0])) {
      7.         if (outvertex.size() != 0) {
      8.             Text vertex = new Text();
      9.             Text lastKeyText = new Text(lastKey);
      10.             Collections.sort(outvertex, new EdgeConvert.ComparatorString());
      11.             for (String vt: outvertex) {
      12.                 vertex.set(vt);
      13.                 context.write(lastKeyText, vertex);
      14.             }
      15.             outvertex = new ArrayList<String>();
      16.         }
      17.     }
      19.     //判断(term[0], term[1])是否是双向边
      20.     boolean flag0 = false, flag1 = false;
      21.     for (Text val: values) {
      22.         if (val.toString().equals("0")) flag0 = true;
      23.         else flag1 = true;
      24.     }
      25.     if (flag0 && flag1) {
      26.         if (degree.get(term[1]) > degree.get(term[0])) {
      27.             outvertex.add(term[1]);
      28.         }
      29.     }
      30.     lastKey = term[0];
      31. }

三、性能分析与优化

3.1 性能分析

  • 该算法的性能瓶颈在遍历每一条边然后边两个端节点对应邻接表的交集，然后对每个顶点出发的邻接表进行排序也比较耗时，算法整体的时间复杂度是O(E1.5)，E为边的数目
  • 目前这个1.0版本的实现鲁棒性比较好，节点编号用Text存储，所以无论节点编号多大都可以存储以及比较，输入的图可以允许重复边的出现，不会影响结果的正确性。但由于mapreduce涉及大量的排序过程，用Text存储节点也就意味着使用字符串排序，字符串之间的比较当然比整型比较开销大，从而会影响程序的整体性能。除此之外，hadoop需要对数据进行序列化之后才能在网络上传输，数据以文本文件输入导致大量的数据序列化转换也会降低程序性能。

3.2 性能优化

2.0版本，在1.0的版本上进行了数据储存和表示方面的优化，相同实验环境(6个Reducer，每个Reducer2G物理内存，Reducer中的java heapsize -Xmx2048m)跑Goolge+数据能快50s左右，具体优化细节如下：

  • 将离散化稀疏的节点转换成顺序化的，这样就可以用IntWritabel表示节点(前提是节点数未超过INT_MAX)而不用Text来表示节点编号，这样就可以避免字符串排序，减少map和reduce阶段的排序开销
  • 将原始Text输入文件转换成Sequence，因为hadoop传输在网络上的数据是序列化的，这样可以避免数据的序列化转换开销。但是由于数据是串行转换的，影响整体性能，但是可以在第一次运行过后存起来，以后运行直接加载sequence的数据文件即可。这一步是和第一步顺序化节点一起完成的，转换后的sequence文件存储的是顺序化的节点表示的边。
  • 在a->b and b->a then a-b的条件下，在获取小度指向大度的边集任务中，mapper需要将一条边的点对合并为key以在reducer中判断是否是双向边，看似只能用Text来存储了，实则这里有一个trick，在对节点顺序化之后的节点数通常不会超过INT_MAX，因此可以使用考虑将两个int型表示的节点转换成long,key存储在高32位，value存储在低32位，通过简单的位操作即可实现，这样mapper输出的key就是long而非Text，从而避免了字符串的比较排序，由于mapreduce涉及大量排序过程，因此在涉及程序的时候尽量用一些trick避免用Text表示key.

四、程序运行结果及时耗

实验环境：CPU型号Intel(R) Xeon(R) CPU E5-2630 v2 @ 2.60GHz，双物理CPU，单CPU6核12线程，所以一共24个虚拟核，程序设置6个reducer，每个reducer配置2GB物理内存，reducer中的java heapsize配置-Xmx2048m

"or"表示if a->b or b->a then a-b的情况，"and"表示if a->b and b->a then a-b的情况

  • 1.0版本的测试结果：
数据集 三角形个数 Driver程序在集群上的运行时间(秒)
Twitter(or) 13082506 127s
Google+(or) 1073677742 278s
Twitter(and) 1818304 125s
Goolge+(and) 27018510 156s
  • 2.0版本的测试结果(不包含输入文件转换的时间)：
数据集 三角形个数 Driver程序在集群上的运行时间(秒)
Twitter(or) 13082506 115s
Google+(or) 1073677742 230s
Twitter(and) 1818304 118s
Goolge+(and) 27018510 181s

评估：2.0版本相对1.0版本在节点数据类型上作了优化，当数据量很大的时候，or情况的性能有显著的提升，Google+数据比1.0版本快了差不多50s左右，但是and情况下2.0版本跑Google+数据性能却下降了，个人猜测可能是job:UnidirectionalEdgeConvert中的Mapper，Reducer，Partitioner，比较函数中涉及大量的位操作或者int与long之间的类型转换，这个开销比1.0版本的对字符串排序开销更大。目前没有很好的想法来避免频繁的位操作与类型转换，有idea的朋友可以给我留言~

基于mapreduce实现图的三角形计数的更多相关文章

  1. MapReduce教程(一)基于MapReduce框架开发<转>

    1 MapReduce编程 1.1 MapReduce简介 MapReduce是一种编程模型,用于大规模数据集(大于1TB)的并行运算,用于解决海量数据的计算问题. MapReduce分成了两个部分: ...

  2. <<一种基于δ函数的图象边缘检测算法>>一文算法的实现。

    原始论文下载: 一种基于δ函数的图象边缘检测算法. 这篇论文读起来感觉不像现在的很多论文,废话一大堆,而是直入主题,反倒使人觉得文章的前后跳跃有点大,不过算法的原理已经讲的清晰了.     一.原理 ...

  3. 基于mapreduce的大规模连通图寻找算法

    基于mapreduce的大规模连通图寻找算法 当我们想要知道哪些账号是一个人的时候往往可以通过业务得到两个账号之间有联系,但是这种联系如何传播呢? 问题 已知每个账号之间的联系 如: A B B C ...

  4. Luogu P2807 三角形计数

    题目背景 三角形计数(triangle) 递推 题目描述 把大三角形的每条边n等分,将对应的等分点连接起来(连接线分别平行于三条边),这样一共会有多少三角形呢?编程来解决这个问题. 输入输出格式 输入 ...

  5. Java实现三角形计数

    题: 解: 这道题考的是穷举的算法. 一开始看到这道题的时候,本能的想到用递归实现.但使用递归的话数据少没问题,数据多了之后会抛栈溢出的异常.我查了一下,原因是使用递归创建了太多的变量, 每个变量创建 ...

  6. 基于MapReduce的贝叶斯网络算法研究参考文献

    原文链接(系列):http://blog.csdn.net/XuanZuoNuo/article/details/10472219 论文: 加速贝叶斯网络:Accelerating Bayesian ...

  7. 洛谷 P2807 三角形计数

    P2807 三角形计数 题目背景 三角形计数(triangle) 递推 题目描述 把大三角形的每条边n等分,将对应的等分点连接起来(连接线分别平行于三条边),这样一共会有多少三角形呢?编程来解决这个问 ...

  8. nvGRAPH三角形计数和遍历示例

    nvGRAPH三角形计数和遍历示例 #include " stdlib.h" #include" inttypes.h" #include" stdi ...

  9. 跟我学Python图像处理丨基于灰度三维图的图像顶帽运算和黑帽运算

    摘要:本篇文章结合灰度三维图像讲解图像顶帽运算和图像黑猫运算,通过Python调用OpenCV函数实现. 本文分享自华为云社区<[Python图像处理] 十三.基于灰度三维图的图像顶帽运算和黑帽 ...

随机推荐

  1. document_index_data.go

    package types type DocumentIndexData struct {     // 文档全文(必须是UTF-8格式),用于生成待索引的关键词     Content string ...

  2. BZOJ_3048_[Usaco2013 Jan]Cow Lineup _双指针

    BZOJ_3048_[Usaco2013 Jan]Cow Lineup _双指针 Description Farmer John's N cows (1 <= N <= 100,000) ...

  3. P2P综述

    原文参见:http://www.lotushy.com/?p=113 [TOC] 什么是P2P P2P全称是Peer-to-peer.P2P计算或P2P网络是一种分布式应用架构.它将任务或负载分发给P ...

  4. ELK 架构之 Elasticsearch、Kibana、Logstash 和 Filebeat 安装配置汇总（6.2.4 版本）

    相关文章: ELK 架构之 Elasticsearch 和 Kibana 安装配置 ELK 架构之 Logstash 和 Filebeat 安装配置 ELK 架构之 Logstash 和 Filebe ...

  5. Vue-CLI和脚手架

    但我们学习Vue时,很多教程都会说到用Vue-CLI构建项目,那么什么是脚手架?什么是Vue-CLI?为什么要用脚手架,好处在哪?以及为何我们用Vue开发项目时要用到Vue-CLI? 首先,CLI为c ...

  6. SpringBoot进阶教程(二十八)整合Redis事物

    Redis默认情况下,事务支持被禁用,必须通过设置setEnableTransactionSupport(true)为使用中的每个redistplate显式启用.这样做会强制将当前重新连接绑定到触发m ...

  7. JDK和Tomcat安装和配置过程

    Jdk: 第一步:在下载JDK 第二步:安装 更改安装路径 *JDK配置: JAVA_HOME 环境变量  D:\jdk1.7.0 CLASSPATH 环境变量   .,%JAVA_HOME%\lib ...

  8. 开源ERP Odoo仓存功能模块深度应用（一）

    基本功能 库位 库位是一个逻辑存货区,可以是一个物理库区,可以是一个货架.货架上的一个货位.库位可以有子库位 库位有虚拟库位和实际库位,实际库位是实际存放货物的库位,虚拟库位是因复式库存记账而虚构的库 ...

  9. 联发科MT8788基带处理器介绍

    MT8788设备具有集成的蓝牙.fm.wlan和gps模块,是一个高度集成的基带平台,包括调制解调器和应用处理子系统,启用LTE/LTE-A和C2K智能设备应用程序.该芯片集成了工作在2.0GHz的A ...

  10. 底部导航栏-----FragmentTabHost

    [说明] 1.主界面上添加父容器:FragmentTabHost 属于v4兼容包 需要指定该id为android:id/tabhost,不能修改,表示由android系统来托管这个id. 本身是一个F ...