组合数取模Lucas定理及快速幂取模

　　组合数取模就是求的值，根据，和的取值范围不同，采取的方法也不一样。

下面，我们来看常见的两种取值情况（m、n在64位整数型范围内）

（1），

此时较简单，在O(n²)可承受的情况下组合数的计算可以直接用杨辉三角递推，边做加法边取模。

（2），，并且是素数

　本文针对该取值范围较大又不太大的情况（2）进行讨论。

这个问题可以使用Lucas定理，定理描述：

　其中

^{这样将组合数的求解分解为小问题的乘积，下面考虑计算}^{C(ni, mi) %p.}

^{已知C(n, m)} ^{mod p = n!/(m!(n - m)!) mod p。当我们要求（a/b）mod p的值，且a很大，无法直接求得a/b的值时，我们可以转而使用乘法逆元k，将a乘上k再模p，即(a*k) mod p。其结果与(a/b) mod p等价。}

^{那么逆元是什么？}

定义：满足a*k≡1 (mod p)的k值就是a关于p的乘法逆元（当p是1时，对于任意a，k都为1）

^{除法取模，这里要用到m!(n-m)!的逆元。}

根据费马小定理：

已知gcd(a, p) = 1，则 a^p-1 ≡ 1 (mod p), 所以 a*a^p-2 ≡ 1 (mod p)。

也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)^{p-2 ；}

下面附上Lucas定理的一种证明，见下图，参考冯志刚《初等数论》第37页。

题意：求，其中，并且是素数。

代码：

#include<iostream>

//#include<algorithm>

using namespace std;

typedef long long ll;

int quick_power_mod(int a,int b,int m){//pow(a,b)%m

    int result = ;

    int base = a;

    while(b>){

         if(b & ==){

            result = (result*base) % m;

         }

         base = (base*base) %m;

         b>>=;

    }

    return result;

}

//计算组合数取模

ll comp(ll a, ll b, int p) {//composite num C(a,b)%p

    if(a < b)   return ;

    if(a == b)  return ;

    if(b > a - b)   b = a - b;

    int ans = , ca = , cb = ;

    for(ll i = ; i < b; ++i) {

        ca = (ca * (a - i))%p;

        cb = (cb * (b - i))%p;

    }

    ans = (ca*quick_power_mod(cb, p - , p)) % p;

    return ans;

}

ll lucas(ll n, ll m, ll p) {

     ll ans = ;

     while(n&&m&&ans) {

        ans = (ans*comp(n%p, m%p, p)) % p;//also can be recusive

        n /= p;

        m /= p;

     }

     return ans;

}

int main(){

    ll m,n;

    while(cin>>n>>m){

        cout<<lucas(n,m,)<<endl;

    }

    return ;

}

上面的代码中用到了求幂取模操作来计算(m!(n-m)!)^p-2 % p.下面解释幂取模算法：

反复平方法求a^b%m

通过研究指数b的二进制表示发现，对任意的整数b都可表示为：

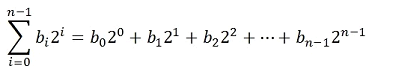
n表示b的实际二进制位数
b_i表示该位是0或1

因此，a^b可表示为：

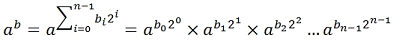
即用b的每一位表示a的每一项，而对任意相邻的两项存在平方关系，即：

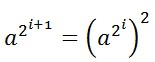
因此我们构造下面的算法：

把b转换为二进制表示，并从右至左扫描其每一位（从低到高）
当扫描到第i位时，根据同余性质（2）计算a的第i项的模：

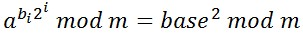
base变量表示第i-1位时计算出的模，通过递归能很容易地确定所有位的模。
如果第i位为1，即b_i=1,则表示该位需要参与模运算，计算结果 result = (result*base) mod m;其中result为前i-1次的计算结果；若b_i=0，则表示a的第i项为1，不必参与模运算

int quick_power_mod(int a,int b,int m){

    int result = 1;

    int base = a;

    while(b>0){

         if(b & 1==1){

            result = (result*base) % m;

         }

         base = (base*base) %m;

         b >>=1;

    }

    return result;

}

其中运用了两个同余性质：

同余性质1：ab≡bc (mod m)

同余性质2： a≡c (mod m) => a²≡c² (mod m)

理解要点：

base记录了a的每项的模，无论b在该位是0还是1，该结果都记录，目的是给后续位为1的项使用，计算方式是前一结果的平方取模，这也是反复平方法的由来
result只记录了位为1的项的模结果，该计算方式使用了同余性质1
通过地把a使用二进制表示，并结合同余性质1，2，巧妙地化解了大数取模的运算。对1024位这样的大数，也最多进行1024次循环便可计算模值，性能非常快。

该方法是许多西方数学家努力的结果，通常也称为Montgomery算法。

（以上部分内容由网络搜集整理而来，不当之处，烦请不吝赐教）