关于单调性优化DP算法的理解

Part1-二分栈优化DP

引入

二分栈主要用来优化满足决策单调性的DP转移式。

即我们设\(P[i]\)为\(i\)的决策点位置，那么\(P[i]\)满足单调递增的性质的DP。

由于在这种DP中，满足决策点单调递增，那么对于一个点来说，以它为决策点的点一定是一段连续的区间。

所以我们可以枚举以哪个点作为决策点，去找到它所对应的以它为决策点的区间。

考虑如何找到一个点的区间：

可以发现，在当前情况下(枚举到以某个点作为决策点的情况下)，该点所对应的区间一定为[L,N].(L可能等于N+1)

那么我们可以用一个栈来存储区间[L,N]中的L，每次新枚举到一个决策点\(i\)，就用栈顶L判断，看L是用原决策点更优，还是用新决策点\(i\)更优。

因为满足决策单调性，所以若用新决策点更优的话，该L就没有意义了，就直接可以从栈顶弹出。

我们一直执行以上操作，直到遇到一个L的原决策点比新决策点\(i\)更优，那么说明这个L还是有意义的，所以不能弹。

然后我们就需要去二分一个点出来作为新的L，使得这个点右边的点以\(i\)为决策点更优，左边的点以\(i\)为决策点更劣。

以上就是二分栈的基本思路。

举个例子：

决策点:1111111111 栈:1(1)

决策点:1112222222 栈:1(1) 4(2)

决策点:1112222233 栈:1(1) 4(2) 9(3)

决策点:1112224444 栈:1(1) 4(2) 7(4)

注：栈里应该有两个信息，一个是L，一个是转移点.

(我们不能维护每个点的转移点，那样会提高时间复杂度)

代码实现思路：

①定义一个队首指针，对于目前枚举到的决策点\(i\)，若\(i\)未被队首指针的区间包含，那么指针前移，直到\(i\)被包含，然后更新\(i\)的DP值。(\(i\)的决策点就是目前队首指针所对应的转移点)

②判断目前栈顶的L以\(i\)为决策点更优，还是以原决策点更优。若以\(i\)更优，弹出栈顶，然后，循环往复②操作。

③对于目前的栈，判断一下，栈是否为空：

• 若为空，直接让新的信息入栈。
• 若不为空，二分新决策点L的位置(此处所有点的原决策点都是目前栈顶的原决策点)，入栈。
  
  (注：记得特判L!=N+1)

小结

对于大多关于二分栈的题，一般是发现有单调性后就直接套版了。

所以在使用二分栈时，一般需要先证明DP的决策单调性(一般使用打表法证明)，限制还是很大。

注：有转移限制的DP对二分栈限制很大，只有在限制也满足单调性的情况下才能用。

(比如CSP2019D2T2划分就可以用类二分栈做法过掉\(O(N*log(N))\)能过的所有点)

#include<cstdio>
#include<algorithm>
using namespace std;
const long long ONE=1;
const int MOD=(1<<30);
const int MAXM=100005;
const int MAXN=40000005;
const long long INF=4e18;
int N,TYP,Pt[MAXN];
long long A[MAXN],Dp[MAXN];
int Stac[MAXN],ID[MAXN],L,R;
void Prepare(){
	scanf("%d%d",&N,&TYP);
	if(TYP==1){
		int X,Y,Z,M;
		int P[MAXM]={0},B[MAXN]={0};
		scanf("%d%d%d%d%d%d",&X,&Y,&Z,&B[1],&B[2],&M);
		for(int i=3;i<=N;i++)B[i]=(ONE*B[i-1]*X+ONE*B[i-2]*Y+Z)%MOD;
		for(int i=1,L,R;i<=M;i++){
			scanf("%d%d%d",&P[i],&L,&R);
			for(int j=P[i-1]+1;j<=P[i];j++)
				A[j]=B[j]%(R-L+1)+L;
		}
		return ;
	}
	for(int i=1;i<=N;i++)
		scanf("%lld",&A[i]);
}
int main(){
	Prepare();
	for(int i=1;i<=N;i++)
		A[i]=A[i-1]+A[i];
	for(int i=1;i<=N;i++){
		while(Stac[L+1]<=i&&L<R)L++;
		long long x=A[i]-A[ID[L]];
		Dp[i]=Dp[ID[L]]+x*x;Pt[i]=ID[i];
		int l=i,r=N+1;
		while(L<=R&&A[Stac[R]]-A[i]>=x)R--;
		if(L>R){Stac[++R]=i+1;ID[R]=i;continue;}
		while(l+1<r){
			int mid=(l+r)/2;
			if(x<=A[mid]-A[i])r=mid;
			else l=mid;
		}
		if(r==N+1)continue;
		Stac[++R]=r;ID[R]=i;
	}
	printf("%lld\n",Dp[N]);
}

例题

其实主要是证单调性，其它的部分都比较版。

T1玩具装箱

(虽说这是个斜率优化板题呢...)

最终核心大意：给出了\(P\)数组与一个常数\(L\)，其中\(P\)数组满足单调递增的性质。

有一个Dp转移式：\(Dp[i]=min\{Dp[j]+(P[i]-P[j]-L)^2\};\)

单调性证明如下：

采用反证：设有\(A,B,C,D(A<B<C<D)\)，其中\(A\)为\(D\)的最优决策点，\(B\)为\(C\)的最优决策点。（即要证明这种情况不存在）

那么有$$Dp[A]+(P[D]-P[A]-L)^2\le Dp[B]+(P[D]-P[B]-L)^2$$

\[Dp[B]+(P[C]-P[B]-L)^2\le Dp[A]+(P[C]-P[A]-L)^2
\]

可以得到：

\[(P[D]-P[A]-L)^2+(P[C]-P[B]-L)^2\le (P[D]-P[B]-L)^2+(P[C]-P[A]-L)^2
\]

化简得：

\[2*(P[B]-P[A])*(P[D]-P[C])\le0
\]

与条件不符，故不存在这种情况，即证明该Dp有决策单调性。

#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=50005;
int N,Len,A[MAXN],Pt[MAXN];
long long S[MAXN],Dp[MAXN];
int Stac[MAXN],ID[MAXN],L,R;
long long W(int i,int j){
	return (S[i]-S[j]-Len)*(S[i]-S[j]-Len);
}
int main(){
	scanf("%d%d",&N,&Len);Len++;
	for(int i=1;i<=N;i++)
		scanf("%d",&A[i]),S[i]=S[i-1]+A[i];
	for(int i=1;i<=N;i++)S[i]+=i;
	for(int i=1;i<=N;i++){
		while(Stac[L+1]<=i&&L<R)L++;
		Dp[i]=Dp[ID[L]]+W(i,ID[L]);
		while(L<=R&&Dp[ID[R]]+W(Stac[R],ID[R])>=Dp[i]+W(Stac[R],i))R--;
		if(R<L)Stac[++R]=i+1,ID[R]=i;
		else{
			int l=i,r=N+1;
			while(l+1<r){
				int mid=(l+r)/2;
				if(Dp[ID[R]]+W(mid,ID[R])>=Dp[i]+W(mid,i))r=mid;
				else l=mid;
			}
			if(r==N+1)continue;
			Stac[++R]=r;ID[R]=i;
		}
	}
	printf("%lld\n",Dp[N]);
	return 0;
}
/*
Dp[i]=Min{Dp[j]+W(i,j)};
*/

T2诗人小G

最终核心大意：给出了\(P\)数组与一个常数\(L\)及一个参数\(K\)，其中\(P\)数组满足单调递增的性质。

有一个Dp转移式：\(Dp[i]=min\{Dp[j]+|P[i]-P[j]-L|^K\};\)

单调性证明如下：(沿用T1的思路)

采用反证：设有\(A,B,C,D(A<B<C<D)\)，其中\(A\)为\(D\)的最优决策点，\(B\)为\(C\)的最优决策点。（即要证明这种情况不存在）

那么有$$Dp[A]+|P[D]-P[A]-L|^K\le Dp[B]+|P[D]-P[B]-L|^K$$

\[Dp[B]+|P[C]-P[B]-L|^K\le Dp[A]+|P[C]-P[A]-L|^K
\]

可以得到：

\[|P[D]-P[A]-L|^K+|P[C]-P[B]-L|^K\le |P[D]-P[B]-L|^K+|P[C]-P[A]-L|^K
\]

然后......

我们设\(X=P[B]-P[A],Y=P[C]-P[B],Z=P[D]-P[C];\)



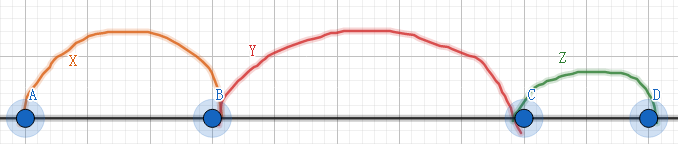
那么有：$$|X+Y+Z-L|^K+|Y-L|K\le |Y+Z-L|^K+|X+Y-L|K$$

我们不妨画出\(F(t)=|t-L|^K\)的图像，就像这样：



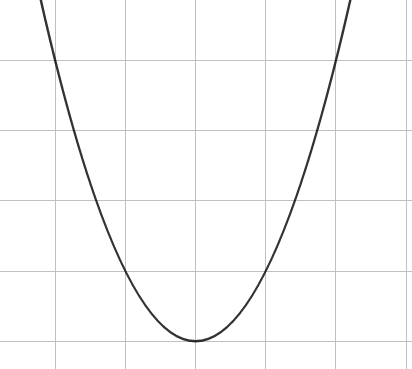
然后在图像上将那四个点标出来。

发现\((X+Y+Z-L)+(Y-L)=(Y+Z-L)+(X+Y-L)\)，即这四个点的横坐标是关于\(E=\frac{X+2*Y+Z}{2}\)对称的。

但由于那四个点的分布情况繁多，所以不妨分类讨论(由于左边右边本质是一样的，所以这里只讨论一边的情况)：

①:左二右二(左边两个点，右边两个点)



这种情况下，显然\(F(Y)+F(X+Y+Z)\ge F(X+Y)+F(Y+Z)\)

故与条件不符。

②:左一右三(左边一个点，右边三个点)



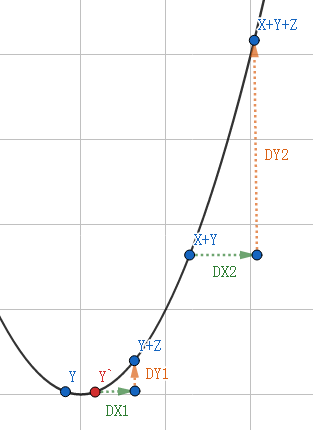
那么这种情况下，我们将\(Y\)翻转至\(Y`\)，那么此时有\(DX1<DX2,DY1<DY2\)，即$$F(Y+Z)-F(Y)=F(Y+Z)-F(Y`)<F(X+Y+Z)-F(X+Y)$$

即有$$F(Y+Z)+F(X+Y)<F(X+Y+Z)+F(Y)$$

故与条件不符。

③:左零右四(左边零个点，右边四个点)

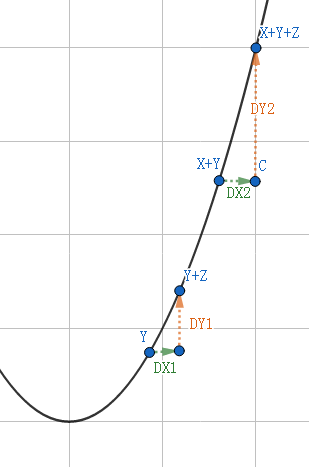
这种情况下有\(DX1=DX2\)，由函数斜率递增的性质可得\(DY1<DY2\)

故同②的情况，与条件不符。

综上，不存在给出情况，故该Dp式满足决策单调性。

(证完单调性后就和玩具装箱一样了，故这里就不给代码了 )

Part2-分治优化DP

引入

其实也没啥好引入的

约束：一般在使用分治优化的时候，DP是满足决策单调性的。

对于形同$$Dp1[i]=max/min{Dp2[j]+W(i,j)};$$这样的DP式子，我们一般是在\(O(N^2)\)出解。(即枚举一个\(i\),一个\(j\))

但是由于满足决策单调性，我们可以这样想：

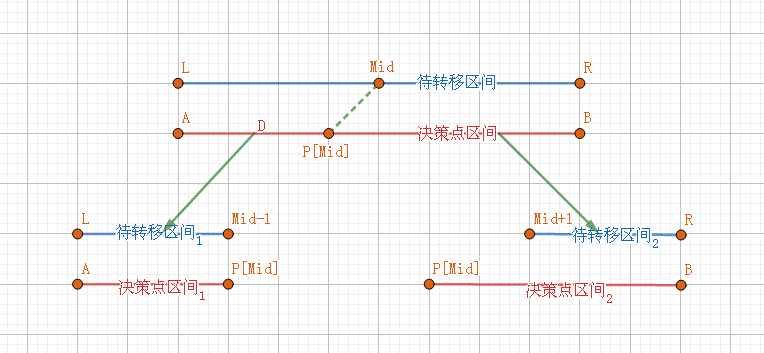
对于\(Dp1\)来说，我们设待转移区间(\(i\))即未更新区间为\([L,R]\)，

设目前可从\(Dp2\)转移过来的点构成的区间(\(j\))即决策点区间为\([A,B]\).

对于普通的转移，我们第一步会枚举一个\(Dp1[i]\)出来进行转移，

但是现在，我们可以使\(i\)变为当前需转移区间\([L,R]\)的中心点\(Mid=\frac{L+R}{2}\)，

即每次转移只转移\(Dp1[Mid]\)，并顺便找出\(Dp1[Mid]\)的决策点\(P[Mid]\).

之后，我们可以把待转移区间\([L,R]\)分为两半：\([L,Mid-1]\)和\([Mid+1,R]\).

而又由于，我们的\(DP\)是满足决策单调性的，所以决策点区间也可以分成两半：\([A,P[Mid]]\)与\([P[Mid],B]\).

然后就可以递推下去了。

又由于我们的DP是满足决策单调性的，所以正确性可以保证。

而在每一层内，决策点总共被枚举次数是\(O(N)\)的，一共有\(log(N)\)层。

故总的时间复杂度是\(O(N*log(N))\).

例题

主要还是证单调性。

T1Ciel and Gondolas

题意，有\(N\)个人，每两个人\(i,j\)之间有\(A[i][j]\)的怨气值。

定义一个组的怨气和为该组内任意两个人的怨气值之和。

现要求将这\(N\)个人分成\(K\)组，使得这\(K\)组的怨气和最小。

问最小怨气和。

好吧，最终DP式子就是：

\[DP[k][i]=min\{DP[k-1][j-1]+\sum_{p=j}^i\sum_{q=p+1}^iA[p][q]\};
\]

单调性的话，证明其实比较简单，这里就不赘述了。

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN=4005;
const int INF=0X3F3F3F3F;
int N,K,A[MAXN][MAXN];
int Dp[MAXN][MAXN];
int Pt[MAXN][MAXN];
inline int Read(){
	register int x=0;
	char c=getchar();bool f=0;
	while(c<'0'||c>'9'){if(c=='-')f^=1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c-'0');c=getchar();}
	if(f==1)x=-x;return x;
}
int W(int i,int j){
	return A[i][i]-A[i][j-1]-A[j-1][i]+A[j-1][j-1];
}
void Solve(int k,int l,int r,int pl,int pr){
	if(l>r)return ;
	int mid=(l+r)/2,pt=pl;
	Dp[k][mid]=INF;
	for(int i=pl;i<=min(mid,pr);i++){
		int cost=Dp[k-1][i-1]+W(mid,i);
		if(cost<Dp[k][mid])Dp[k][mid]=cost,pt=i;
	}
	Solve(k,l,mid-1,pl,pt);
	Solve(k,mid+1,r,pt,pr);
}
int main(){
	N=Read();K=Read();
	for(int i=1;i<=N;i++)
		for(int j=1;j<=N;j++){
			A[i][j]=Read();
			A[i][j]+=A[i][j-1]+A[i-1][j]-A[i-1][j-1];
		}
	for(int i=1;i<=N;i++)Dp[0][i]=INF;
	for(int k=1;k<=K;k++)Solve(k,1,N,1,N);
	printf("%d\n",Dp[K][N]/2);
}

T2The Bakery

题意，给出\(N\)个数，现让你将这\(N\)个数划分为\(K\)段，

定义某一段的代价为该段内不同元素的个数，求最大总代价。

通过以上描述，易得最终DP式为：

\[DP[k][i]=max\{DP[k-1][j-1]+W(i,j)\};
\]

其中\(W(i,j)\)表示\([j,i]\)中不同的数的个数。

关于这个DP式的单调性，我们可以这样想：

设有\(A,B,C,D(A<B<C<D)\)四个数，

其中\(A\)为\(D\)的最优决策点，\(B\)为\(C\)的最优决策点。

那么相应的，就有

\[DP[k-1][B-1]+W(C,B)>DP[k-1][A-1]+W(C,A)
\]

\[DP[k-1][A-1]+W(D,A)>DP[k-1][B-1]+W(D,B)
\]

即有：

\[W(D,A)+W(C,B)>W(C,A)+W(D,B)
\]

我们可以这样想，将\([A,D]\)这个区间分成如下几个部分：



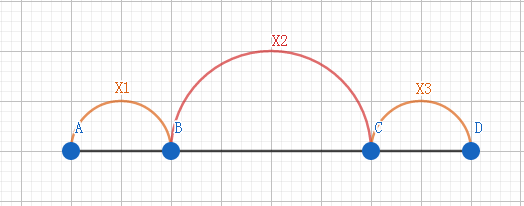
其中\(X2\)表示\(W(C,B)\)的值，

而\(X1,X3\)分别表示\([A,B],[C,D]\)中与\([B,C]\)间不同的数。

即：\(X1+X2=W(C,A),X3+X2=W(D,B)\)

那么$$W(D,A)+W(C,B)>W(C,A)+W(D,B)$$

这个式子就可以写作：

\[W(D,A)>X1+X2+X3
\]

而上式显然不成立，故该DP满足决策单调性。

---

讨论了DP的决策单调性，那么是否可以直接套用之前的板呢?

然而不行，发现在以下板块时：

void Solve(int k,int l,int r,int pl,int pr){
	if(l>r)return ;
	int mid=(l+r)/2,pt=pl;
	Dp[k][mid]=-INF;
	for(int i=pl;i<=min(mid,pr);i++){
		int cost=Dp[k-1][i-1]+W(mid,i);
		if(cost>=Dp[k][mid])Dp[k][mid]=cost,pt=i;
	}
	Solve(k,l,mid-1,pl,pt);
	Solve(k,mid+1,r,pt,pr);
}

我们算\(W(mid,i)\)无法\(O(1)\)出解，同时有一个处理思路就是：

void Solve(int k,int l,int r,int pl,int pr){
	if(l>r)return ;
	int mid=(l+r)/2,pt=pl;
	Dp[k][mid]=-INF;
	for(int i=mid;i>pr;i--)Tur(i);
	for(int i=min(mid,pr);i>=pl;i--){
		Tur(i);int cost=Dp[k-1][i-1]+Cnt;
		if(cost>=Dp[k][mid])Dp[k][mid]=cost,pt=i;
	}
	Solve(k,l,mid-1,pl,pt);
	Solve(k,mid+1,r,pt,pr);
}

其中,Tur(i)表示更新某一元素入答案中。

但是这样做会多增加\([pr+1,mid]\)的循环，从而增加时间复杂度。

从而被恶意出题人卡成TLE...

针对于以上情况，我们可以使用一种类似于滑动的思想。

即使用两个指针\(L,R\)，然后维护区间\(W(L,R)\)的值。

每次要求某个\(W(l,r)\)的时候，就将\(L\)滑动到\(l\)，\(R\)滑动到\(r\)，滑动途中维护\(W(L,R)\)就行了。

void Tur(int x,int k){
	CCnt[Val[x]]+=k;
	if(CCnt[Val[x]]==0&&k==-1)Cnt--;
	if(CCnt[Val[x]]==1&&k==1)Cnt++;
}
long long W(int r,int l){
	while(L>l)Tur(--L,1);
	while(R<r)Tur(++R,1);
	while(L<l)Tur(L++,-1);
	while(R>r)Tur(R--,-1);
	return Cnt;
}
void Solve(int k,int l,int r,int pl,int pr){
	if(l>r)return ;
	int mid=(l+r)/2,pt=pl;
	Dp[k][mid]=-INF;
	for(int i=min(mid,pr);i>=pl;i--){
		long long cost=Dp[k-1][i-1]+W(mid,i);
		if(cost>=Dp[k][mid])Dp[k][mid]=cost,pt=i;
	}
	Solve(k,l,mid-1,pl,pt);
	Solve(k,mid+1,r,pt,pr);
}

而这样的时间复杂度也是\(O(N*log(N))\)的。

原因如下：

首先，由于我们函数的递推结构是先左再右，

所以我们的\(L\)指针移动的总步数是\(O(N)\)范围的。

同时，我们每次走的区间都是连续的，而对于任意一个位置，我们最多只会经过\(O(log(N))\)次。

所以，时间复杂度还是\(O(N*log(N))\)的。

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXK=55;
const int MAXN=35005;
const long long INF=1e18;
int T,N,K,L,R,Ans;
int Val[MAXN],Cnt,CCnt[MAXN];
long long Dp[MAXK][MAXN];
inline int Read(){
	register int x=0;
	char c=getchar();bool f=0;
	while(c<'0'||c>'9'){if(c=='-')f^=1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c-'0');c=getchar();}
	if(f==1)x=-x;return x;
}
void Tur(int x,int k){
	CCnt[Val[x]]+=k;
	if(CCnt[Val[x]]==0&&k==-1)Cnt--;
	if(CCnt[Val[x]]==1&&k==1)Cnt++;
}
long long W(int r,int l){
	while(L>l)Tur(--L,1);
	while(R<r)Tur(++R,1);
	while(L<l)Tur(L++,-1);
	while(R>r)Tur(R--,-1);
	return Cnt;
}
void Solve(int k,int l,int r,int pl,int pr){
	if(l>r)return ;
	int mid=(l+r)/2,pt=pl;
	Dp[k][mid]=-INF;
	for(int i=min(mid,pr);i>=pl;i--){
		long long cost=Dp[k-1][i-1]+W(mid,i);
		if(cost>=Dp[k][mid])Dp[k][mid]=cost,pt=i;
	}
	Solve(k,l,mid-1,pl,pt);
	Solve(k,mid+1,r,pt,pr);
}
int main(){
	N=Read();K=Read();
	for(int i=1;i<=N;i++)Val[i]=Read();
	for(int i=1;i<=N;i++)Dp[0][i]=-INF;
	for(int k=1;k<=K;k++)Solve(k,1,N,1,N);
	printf("%lld\n",Dp[K][N]);
}

后记

打表法好啊。。。