算法：九宫格问题--奇数阶魔方（Magic-Square）

一、魔方介绍

　　魔方（这里是简称，也可以叫幻方、魔术矩阵，Magic Square）是 n×n 正方形网格（n 为每侧的单元数），里面每个单元格填充了不同的正整数 1, 2, 3, ... , n₂，并且每一行、每一列和对角线中的正整数之和相等。每行、每列以及对角线上的单元格里的正整数之和又叫做魔术常数或魔方的魔术和。

幻方历史：

　　《系辞》云：“河出图，洛出书，圣人则之。”在宋朝之前，洛书的记述只有文字。

　　九宫图实物最早发现于西汉，1977年中国考古学家在安徽阜阳县双古堆西汉古墓中发现汉文帝七年（前173年）的太乙九宫占盘，乃是中国汉代幻方的实物。东汉《数术记遗》也有记载。

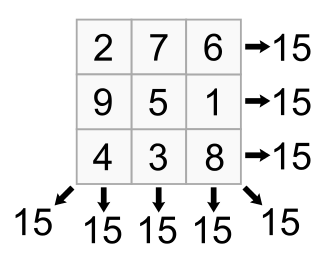
　　后来陈抟以降认为河图洛书的洛书代表九宫图，为 1...9 这 9 个数，而 3 行、3 列以及两对角线上各自的数之和均为 15。

二、奇数阶幻方构造法

　　幻方可以使用 N 阶方阵来表示，方阵的每行、每列以及两条对角线的和都等于常数 M₂(N)，如果填充数为 1, 2, ... , N²，那么有

　　三个成立条件：

1. 下一个数字的位置是通过将前一个数字的行号减 1，再将前一个数字的列号加 1来计算的。在任何时候，如果计算出的行位置变为 -1，它将绕到 n - 1。同样，如果计算出的列位置变为 n，则它将绕到 0。
2. 如果幻方在计算位置处已经包含数字，则计算列位置将减少 2，计算行位置将增加 1。
3. 如果计算出的行位置为 -1 且计算出的列位置为 n，则新位置将为：(0, n-2)。

　　其时间复杂度为 O(n²)。

三、奇数阶幻方构造代码

 1 package algorithm;
 2
 3 /**
 4  * 奇数阶魔方矩阵
 5  */
 6 public class MagicSquare {
 7     /**
 8      * 生成奇数阶魔方矩阵(n*n), 魔方里面填充范围内不同的正整数：1, 2, 3, ... , n^2
 9      *
10      * @param n 奇数阶
11      */
12     private static void generateSquare(int n) {
13         int[][] magicSquare = new int[n][n];
14
15         /**
16          * 初始化正整数1的位置
17          */
18         int i = n / 2;  // row
19         int j = n - 1;  // column
20
21         /* 把一个个树填充进魔方中 */
22         for (int num = 1; num <= n * n;) {
23             if (i == -1 && j == n) { // 条件3
24                 j = n - 2;
25                 i = 0;
26             } else {
27                 if (j == n)　　// 条件1
28                     j = 0;
29                 if (i < 0)
30                     i = n - 1;
31             }
32
33             if (magicSquare[i][j] != 0) {　　// 条件2
34                 j -= 2;
35                 i++;
36                 continue;
37             } else {
38                 magicSquare[i][j] = num++;  // 把一个个正整数填进对应位置
39             }
40             j++;
41             i--;
42         }
43
44         System.out.println("The Magic Square for " + n + ":");                          // 打印魔方的阶数
45         System.out.println("Sum of each row or column " + (n * (n * n + 1) / 2) + ":"); // 打印此魔方的魔术常数，即每行、每列、对角线之和
46
47         /* 打印魔方方阵 */
48         for (i = 0; i < n; i++) {
49             for (j = 0; j < n; j++) {
50                 System.out.print(magicSquare[i][j] + " ");
51             }
52             System.out.println();
53         }
54     }
55
56     public static void main(String[] args) {
57         /* n为奇数时有效 */
58         int n = 5;
59         generateSquare(n);
60     }
61 }