2021CCPC网络赛（重赛）题解
自己还是太菜了，五个小时一个题也没磕出来，还是队友牛逼！...
Primality Test
先看这个题，可能一上去就被\(\frac{f(x)+f(f(x))}{2}\)向下取整吓住了，但仔细想想，\(f(x)\)与\(f(f(x))\)不是相邻的质数吗？那么除2，向下取整，落点一定在两者之间，那么一定是合数。当然除了2,3的特例，这种特判下即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
int T;cin>>T;
while(T--)
{
ll x;cin>>x;
if(x==1) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
Nun Heh Heh Aaaaaaaaaaa
为什么这么简单的题，我当初看了那么长的时间都没看出来。
发现这个题的主要难点在于以当前i(c[i]='h')为结尾的字串为nunhehheh的方案数。我们大胆的设状态，仔细考虑dp所代表的的集合，以及进行转移。设f[i][j]表示前i位，其中第i位匹配到nunhehheh的第j位的方案数。那么若c[i]=s[j]，我们考虑枚举上一个字符也就是s[j-1]出现的位置，f[i][j]=f[k][j-1].其中c[k]==s[j-1].但这种方法显然是O(n^2)的。考虑转移时，其实f[k][j-1],只要是j-1即可，我们大可以用一个数组g[j]表示前i个字符中以某个点为j结尾的方案数。这样的话转移时就是O(1)的。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+10,P=998244353;
int T,n,f[N][12],cnt[N],g[12];
char c[N];
string s;
inline ll power(ll x,ll y)
{
ll ans=1;
while(y)
{
if(y&1) ans=ans*x%P;
y>>=1;
x=x*x%P;
}
return ans%P;
}
inline void clear()
{
for(int i=0;i<=n+1;++i)
{
cnt[i]=0;
for(int j=0;j<=10;++j) f[i][j]=0;
}
memset(g,0,sizeof(g));
}
int main()
{
//freopen("1.in","r",stdin);
scanf("%d",&T);
s="2nunhehheh";
while(T--)
{
scanf("%s",c+1);
n=strlen(c+1);
clear();
for(int i=n;i>=1;--i)
{
cnt[i]=cnt[i+1];
if(c[i]=='a') cnt[i]++;
}
ll ans=0;
for(int i=1;i<=n;++i)
{
for(int j=9;j>=1;--j)//匹配nunhehheh的每一位。
{
if(c[i]==s[j])
{
f[i][j]=g[j-1];
if(j==1) f[i][j]=1;
g[j]=(g[j]+f[i][j])%P;
if(j==9) ans=(ans+(ll)f[i][j]*(power(2,cnt[i])-1)%P)%P;
}
}
}
printf("%lld\n",ans);
}
return 0;
}
Monopoly
哎呀，这个题，感觉自己当时的思路已经很接近了，但是还是输给了对于分类讨论的复杂性的恐惧，加上当时没有一个完整的思路进行支撑，就弃疗了。
首先我们设\(S\)为整个序列的和，\(s_i\)为第i位的前缀和，那么可以有这个式子\(s_i+kS=x(k>=0,1\leq i\leq n)\)，其中只有\(S,x\)已知，我们做适当的调整，\(kS=x-s_i\)，这样的话\(x-s_i\)必须是\(S\)的正整数（以及0）的倍数。那么可以想到\(x,s_i\)对\(S\)同余，也就是说余数相同。这样的话，我们可以对\(s_i\)根据对\(S\)的余数进行分类，每次询问的x只在模数相同的一类中找。接下来考虑最小化\(i+k*n\)的值，这个时候我们可以讨论S>0，那么为了满足倍数的关系，必须满足\(s_i\leq x\)，同时为了k足够小，我们需要找到的\(s_i\)足够大，(你把这个过程放在数轴上想)。也就是小于等于x的最大值。这不是二分吗？我们再在每一类中进行排序，直接二分查找即可。接下来考虑S<0的情况，我们可以将序列中的每个数取反，再将x取反即可。注意当S=0时，系统会报错，单独讨论这种情况。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+10;
int T,n,m,num;
map<ll,int>mp;//map表示序列号。
map<ll,int>id[N];//余数为i的数字为j的最小的i。
vector<ll>ve[N];
ll s[N];
inline void clear()
{
mp.clear();num=0;
for(int i=0;i<=n;++i)
{
s[i]=0;
id[i].clear();
ve[i].clear();
}
}
inline void solve()
{
mp[0]=0;
for(int i=1;i<=n;++i)
{
if(mp.find(s[i])==mp.end())
mp[s[i]]=i;
}
for(int i=1;i<=m;++i)
{
ll x;scanf("%lld",&x);
if(mp.find(x)==mp.end()) puts("-1");
else printf("%d\n",mp[x]);
}
}
int main()
{
// freopen("1.in","r",stdin);
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m);
clear();
for(int i=1;i<=n;++i)
{
ll x;scanf("%lld",&x);
s[i]=s[i-1]+x;
}
if(s[n]==0) {solve();continue;}
int op=1;if(s[n]<0) op=-1;
ll S=s[n]*op;
for(int i=0;i<=n;++i)
{
s[i]*=op;
ll ps=(s[i]%S+S)%S;
if(mp.find(ps)==mp.end()) mp[ps]=++num;
if(id[mp[ps]].find(s[i])==id[mp[ps]].end())
{
id[mp[ps]][s[i]]=i;
ve[mp[ps]].push_back(s[i]);
}
}
for(int i=1;i<=num;++i) sort(ve[i].begin(),ve[i].end());
for(int i=1;i<=m;++i)
{
ll x;scanf("%lld",&x);
x*=op;
if(x==0) {puts("0");continue;}
ll ps=(x%S+S)%S;
if(mp.find(ps)==mp.end()||ve[mp[ps]][0]>x) {puts("-1");continue;}
int j=mp[ps];
int k=upper_bound(ve[j].begin(),ve[j].end(),x)-ve[j].begin()-1;
ll so=ve[j][k];
ll ans=id[j][so]+((x-so)/S)*n;
printf("%lld\n",ans);
}
}
return 0;
}
Jumping Monkey
这个题当初还是队友做出来的，自己主要是思路就没想到那一块去。由于每次从一个点出发一直跳，跳的最多的点的个数，想想其实问你的就是从这个点出发能跳到哪些点去，因为这些点我们可以按点权从小到大排序依次跳就完事了。当初困在了DP的思维上，想不出来好的转移方式。后来看了看题解大大的做法，其实是图论的知识吧，也不对就是思维的问题吧。我们考虑先将所有的点从小到大排序，依次考虑每个点能否到达点i，这样点i一定比之前的点权大，只要联通即可。也就是重新建图加边的问题。考虑当前是一个空白的图，我们依次将每个点加进去，考虑哪些点能到达当前这个点的话，就是连通块的问题，若当前点能够连到某个连通块，则这个连通块内的所有点都能到达这个点，那么这些点的答案都加1.然后将这个点及其连到的点合并成一个新的连通块即可。考虑整个需要我们维护的操作就是加上点，连通块整个的值加1，合并连通块。对于连通块的做法，我只会并查集，其实并查集就是维护连通块是否联通的问题，顺带记录一些信息。接下来就是这个题的精妙之处，我们发现，我们每次都是将一个连通块的值都加1，我们可以将加进去的点i当做根节点，这样的话那些连通块的深度就加1，符合我们的要求，我们只需要将点i向原本这个连通块的根节点连边即可。但这样不就打乱了原本的土的结构了吗？其实我们没必要维护原本的土的结构，我们还需要在一个点i加进去之后，那些连通块的点都可以加1就行。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int T,n,f[N],a[N],b[N],d[N];
vector<int>son[N];
vector<int>bian[N];
map<pair<int,int>,bool>mp;
inline void clear()
{
mp.clear();
for(int i=1;i<=n;++i)
{
son[i].clear();
bian[i].clear();
f[i]=i;b[i]=i;
d[i]=0;
}
}
inline bool cmp(int x,int y) {return a[x]<a[y];}
inline int getf(int x) {return f[x]==x?x:f[x]=getf(f[x]);}
inline void dfs(int x)
{
for(auto y:bian[x])
{
d[y]=d[x]+1;
dfs(y);
}
}
int main()
{
// freopen("1.in","r",stdin);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
clear();
for(int i=1;i<n;++i)
{
int x,y;scanf("%d%d",&x,&y);
son[x].push_back(y);
son[y].push_back(x);
}
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
sort(b+1,b+n+1,cmp);
for(int i=1;i<=n;++i)//依次加入每一个点。
{
int x=b[i];
for(auto y:son[x])//遍历i的每一个出边
{
if(a[y]>a[x]) continue;
int t=getf(y);
if(mp.find({x,t})==mp.end())
{
mp[{x,t}]=1;
bian[x].push_back(t);
f[t]=x;
}
}
}
d[b[n]]=1;
dfs(b[n]);
for(int i=1;i<=n;++i) printf("%d\n",d[i]);
}
return 0;
}
Public Transport System
这个题当初也是想了好久没出来，显然因为如果\(a_i>a_{i-1}\)的话我们走当前的边权的值就为\(a_i-b_i\)，这就使得我们必须记录当前点的上一条边是哪一条，想了想，其实所有的状态数也不多，即m个状态，毕竟只有m条边，每条边对应一个状态。但这个记录就只能用map实现，如果再跑dijkstra总的复杂度为O(mlognlogm)，m的范围为\(1.2\times10^6\)，这算出来，\(6\times10^9\),好吧，我觉得出题人肯定就是专门卡这个暴力的....
瞅瞅题解大大的做法，原来是要重新建图，又是建图的问题，这种题不是只在网络流中考察吗？好吧，这次确实拓了眼界。首先先将两种边分开，因为两种边权的图，毕竟没有单边权的方便。考虑边权\(a_i\)的边，我们没什么限制条件，但对于边权为\(a_i-b_i\)的边，我们必须满足一定条件，也就是前一条边的\(a_i\)必须小于当前的\(a_i\)。我们可以发现由于一个之前的边对应的可走的边权为\(a_i-b_i\)的边的\(a_i\)是在一个区间的，所以这就给我们的优化带来了可能。（不是我说的，是题解说的。）具体的，我们可以这样做：首先设d为当前点x的出度，我们将x拆分成d+1个点，\(（x_0,x_1,x_2,...,x_d）\),让他们分别管理这些\(a_i-b_i\)出边，其中所有边权为\(a_i\)的边由\(x_0\)管理。我们将x所有边权为\(a_i-b_i\)的出边按照\(a_i\)的从大到小排序，接下来将他们依次交给\(x_i\)管理(也就是\(x_i\)连排过序后为i的边)。我们接下来i从0到d-1，从\(x_{i+1}\)向\(x_{i}\)连边权为0的边。这样由于提前排过序，能从小的\(a_i\)走\(a_i-b_i\)的特殊边，一定能从大的\(a_i\)走\(a_i-b_i\)的特殊边。之后我们只需要根据每个入边找到相对应能走的最大的\(x_i\)，满足它所管理的边的\(a_i\)大于他的入边即可。
具体的如下图：
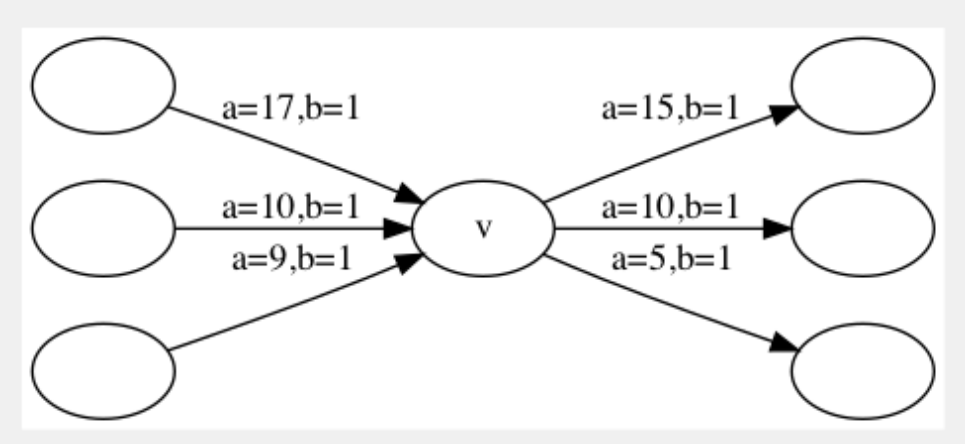
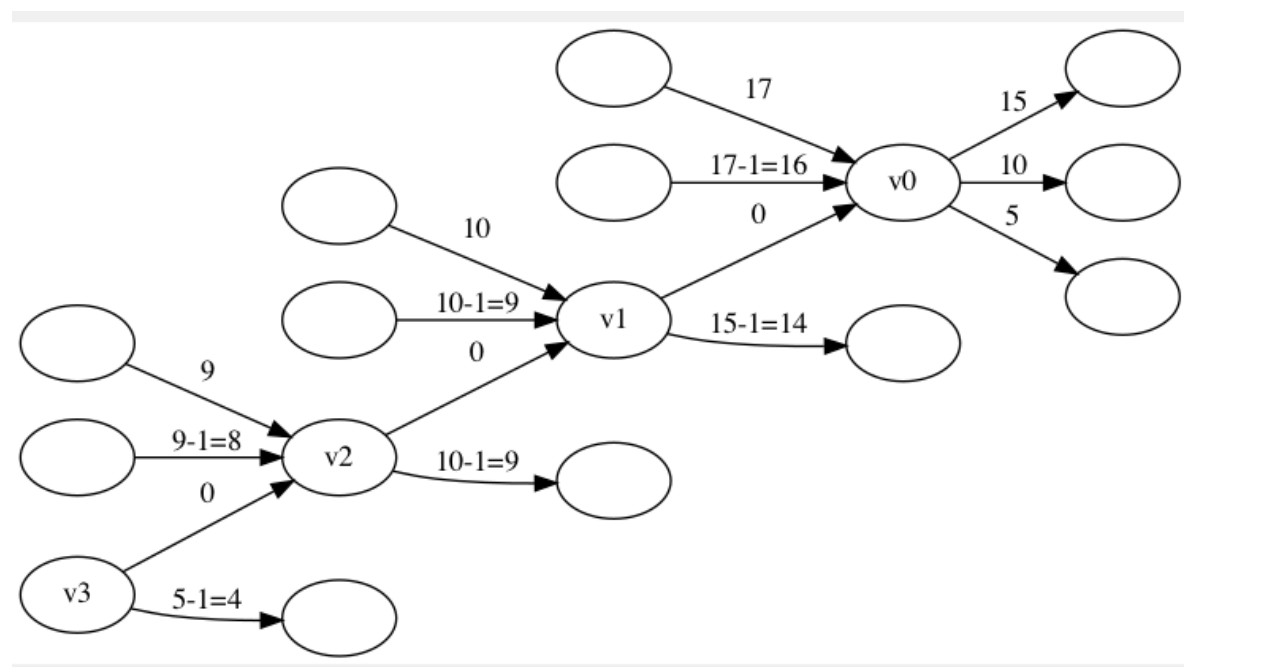
这样，一共的点为n+m,一共的边为2*m,即使m是\(1.2\times 10^6\)的数据量，我们跑dijkstra也完全没有问题。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e5+10;
int du[N],n,m,l[N],link[N],tot,vis[N];
ll dis[N];
//l[i]记录每个点拆出来的d+1个点的第一个点的编号。
vector<int>son[N];//记录每个点，对应的边的编号。
struct bian{int x,y,A,B;}b[N];
struct wy{int y,v,next;}a[N<<1];
priority_queue<pair<ll,int> >q;
inline void add(int x,int y,int v)
{
a[++tot].y=y;a[tot].v=v;a[tot].next=link[x];link[x]=tot;
}
inline void clear()
{
tot=0;
for(int i=1;i<=n+m;++i) link[i]=0;
for(int i=1;i<=n;++i) son[i].clear(),du[i]=0;
}
inline bool cmp(int x,int y)
{
return b[x].A>b[y].A;
}
inline int find(int x,int A)//有一个ai的入边应该连向点x中的哪个点
{
if(!du[x]||A>=b[son[x][0]].A) return l[x];//返回x0的情况。
int L=0,R=du[x]-1;
while(L<R)//在x的边中查找>A的最小的边。
{
int mid=L+R+1>>1;
if(b[son[x][mid]].A>A) L=mid;
else R=mid-1;
}
return l[x]+L+1;
}
inline void dijkstra()
{
while(q.size()) q.pop();
for(int i=1;i<=n+m;++i)
{
dis[i]=1e18;
vis[i]=0;
}
dis[l[1]]=0;q.push({0,l[1]});
while(!q.empty())
{
int x=q.top().second;q.pop();
if(vis[x]) continue;
vis[x]=1;
for(int i=link[x];i;i=a[i].next)
{
int y=a[i].y;
if(dis[x]+a[i].v<dis[y])
{
dis[y]=dis[x]+a[i].v;
q.push({-dis[y],y});
}
}
}
}
int main()
{
// freopen("1.in","r",stdin);
int T;scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m);
clear();
for(int i=1;i<=m;++i)
{
scanf("%d%d%d%d",&b[i].x,&b[i].y,&b[i].A,&b[i].B);
son[b[i].x].push_back(i);
du[b[i].x]++;
}
for(int i=1;i<=n;++i)
{
if(son[i].size())
sort(son[i].begin(),son[i].end(),cmp);
}
int num=0;
for(int i=1;i<=n;++i) //给每个点分配编号且处理内部的边。
{
l[i]=++num; //l[i] - l[i]+du[i]是这个点所有拆出来的点的编号。
for(int j=du[i];j>=1;--j) add(l[i]+j,l[i]+j-1,0);
num+=du[i];
}
for(int i=1;i<=n;++i)//处理点i的所有边
{
int js=son[i].size();
for(int j=0;j<js;++j)//枚举i的所有出边
{
int id=son[i][j];
int y=find(b[id].y,b[id].A);
add(l[i],y,b[id].A);//先处理边权为ai的。
add(l[i]+j+1,y,b[id].A-b[id].B);
}
}
dijkstra();
for(int i=1;i<=n;++i)
{
if(dis[l[i]]==1e18) dis[l[i]]=-1;
printf("%lld",dis[l[i]]);
if(i!=n) printf(" ");
}
printf("\n");
}
return 0;
}
2021CCPC网络赛（重赛）题解的更多相关文章
- PTA|团体程序设计天梯赛-练习题目题解锦集（C/C++）（持续更新中……）
PTA|团体程序设计天梯赛-练习题目题解锦集(持续更新中) 实现语言:C/C++: 欢迎各位看官交流讨论.指导题解错误:或者分享更快的方法!! 题目链接:https://pintia.cn/ ...
- 2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 F Color it
链接:https://www.nowcoder.com/acm/contest/163/F 来源:牛客网 2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 F Color it 时间限制:C ...
- ACdream区域赛指导赛之专题赛系列(1)の数学专场
Contest : ACdream区域赛指导赛之专题赛系列(1)の数学专场 A:EOF女神的相反数 题意:n(<=10^18)的数转化成2进制.翻转后(去掉前导零)输出十进制 思路:water ...
- 2018 ACMICPC上海大都会赛重现赛 H - A Simple Problem with Integers (线段树，循环节)
2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 H - A Simple Problem with Integers (线段树,循环节) 链接:https://ac.nowcoder.co ...
- 2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 F Color it (扫描线)
2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 F Color it (扫描线) 链接:https://ac.nowcoder.com/acm/contest/163/F来源:牛客网 时间 ...
- 2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 J Beautiful Numbers (数位DP)
2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 J Beautiful Numbers (数位DP) 链接:https://ac.nowcoder.com/acm/contest/163/ ...
- 2018 ICPC上海大都会赛重现赛 D Thinking-Bear magic (几何)
2018 ACM 国际大学生程序设计竞赛上海大都会赛重现赛 D Thinking-Bear magic (几何) 链接:https://ac.nowcoder.com/acm/contest/163/ ...
- 2017南开ACM校赛（网络赛） 民间题解
orz 首先说一下这个只是民间题解,可能会有很多错误 程序还没有评测,所以可能存在问题 C题比赛的时候没想到..后来发现是个模板题,所以没有代码 希望这份题解能对读者有所启发吧... A题 直接倒序枚 ...
- 2016 ACM-ICPC 青岛站网络赛G题 题解
[参考博客][https://blog.csdn.net/Tawn0000/article/details/82255682] 题意: 将n个数按照每k个一组来合并,合并需要花费的cost是两个数的长 ...
随机推荐
- Python中with...as...的用法详解
简介 with是从Python2.5引入的一个新的语法,它是一种上下文管理协议,目的在于从流程图中把 try,except 和finally 关键字和资源分配释放相关代码统统去掉,简化try-.exc ...
- Windows难民安装docker的注意事项
Windows下如何安装docker,这个没啥可说的,一直下一步就ok Windows docker 下载地址: https://download.docker.com/win/stable/Doc ...
- TP5 pc和wap跳转404
在config.php中配置 // HttpException异常 'http_exception_template' => [ // 定义404错误的重定向页面地址 404 => isW ...
- php 开启报错
// 开启报错提醒ini_set("display_errors", "On");error_reporting(E_ALL | E_STRICT); // 某 ...
- nginx使用用户真实IP做hash（解决经过CND后ip_hash失效问题）
在nginx中常用的有以下四种负载均衡的算法,分别是:round-robin.ip-hash.least-connected和weighted.当然在实际生产中或许使用最多的就是ip-hash了,一般 ...
- js中date类型的格式转化为yyyy-MM-dd HH:mm:ss的String类型
在vue中或其他框架中可以在Date的原型链中添加Format的方法,如ruoyi可以写在main.js中更好,如果写在utils还需要去导入包. 正常的js直接放到utils.js就好 Date.p ...
- mogoose 创建数据库并增删改查
下载 npm i mongoose -s 连接数据库 const mongoose = require("mongoose"); mongoose.connect(dbURL); ...
- session与cookie的联系与区别
一.Session与Cookie介绍 这些都是基础知识,不过有必要做深入了解.先简单介绍一下. 二者的定义: 当你在浏览网站的时候,WEB 服务器会先送一小小资料放在你的计算机上,Cookie 会帮你 ...
- 启动jemeter 报错相关解决方案
1:当启动jemeter时报错"页面文件太小,无法完成操作" 如图: 是说明分配的内容不足,即可调整内存重启即可解决 1):打开:控制面板>系统和安全>系统 2):点击 ...
- 鸿蒙内核源码分析(源码注释篇) | 鸿蒙必定成功，也必然成功 | 百篇博客分析OpenHarmony源码 | v13.02
百篇博客系列篇.本篇为: v13.xx 鸿蒙内核源码分析(源码注释篇) | 鸿蒙必定成功,也必然成功 | 51.c.h .o 几点说明 kernel_liteos_a_note | 中文注解鸿蒙内核 ...