Unsupervised Feature Learning via Non-Parametric Instance Discrimination

目录

• 概
• 主要内容

Wu Z., Xiong Y., Yu S. & Lin D. Unsupervised Feature Learning via Non-Parametric Instance Discrimination. arXiv preprint arXiv 1805.01978

概

这篇文章也是最近很虎的contrastive learning的经典之作, 其用于下游任务的处理虽没现在的简单粗暴, 但效果依然很好.

主要内容

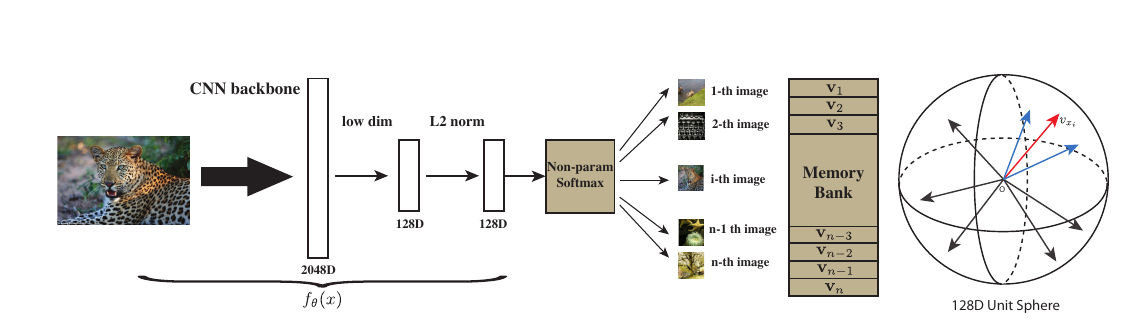
因为作者实际上是从一个无监督的角度去考虑的, 其出发点就是, 如果希望将分类器将每一个样本都区分开来, 是否能够获得比较好的特征呢? 输入\(x\)经过embedding function 得到\(f_{\theta}(x)\), 即特征, 那么现在的问题是:

• 目标是将所有样本作为一个单独的类别, 这就会导致类别个数很大, 甚至成百上千万, 如果这是还和普通的分类任务一样, 将

\[P(i|x) = \frac{\exp (w_i^T f_{\theta}(x))}{\sum_{i=1}^n \exp (w_j^T f_{\theta}(x))},
\]

​ 则最后一个分类层的权重\(W \in \mathbb{R}^{k \times n}\), 这将是无法承受的存储量和计算量.

为了解决这个问题, 作者选择的首先构造一个memory bank, 将特征存储起来, 第\(i\)个样本对应的为\(v_i\), 而当前\(f_{\theta}(x_i)\)记作\(f_i\), 则

\[P(i|x) = \frac{\exp (f_{\theta}(x)^Tv_i/\tau)}{\sum_{j=1}^n\exp(f_{\theta}(x)^T v_j / \tau)},
\]

这里\(\tau\)是temperature.

这样就避免了\(w\), 且符合直觉: 即衡量了\(f_{\theta}(x)\)与数据中的第\(i\)个样本的相关度. 但是, 虽然这一定程度上减少了存储量, 但是计算量并没有减少, 即我们需要估计分母\(Z_i\), 实际上, 这就是一个配平的问题, 这是负样本采样可以发挥作用的地方.

假设

\[h(i, v) := P(D=1|i,v) = \frac{P(i|v)}{P(i|v)+m P_n(i)},
\]

其中\(P_n(i)\)为一个均匀分布, 即每个特征被选中的概率为\(\frac{1}{n}\). 然后便是经典的损失

\[\mathcal{J}_{NCE} (\theta) = -\mathbb{E}_{P_d} [\log h(i, v)] - m \cdot \mathbb{E}_{P_n}(\log (1 -h(i,v'))).
\]

个人感觉: \(P_d(i, v) = P(v) \cdot Q(i|v)\), 其中\(Q(i|v)\)仅当\(v\)为第\(i\)个样本点的特征是概率为\(1\)否则为\(0\). 而\(P_n(i, v) = P(v) \cdot \frac{1}{n}\). 同时, 估计

\[Z_i \approx \frac{n}{m} \sum_{k=1}^m \exp(v_{jk}^T f_i/\tau),
\]

感觉就像是一个抽样. 这个\(\frac{n}{m}\)最新的文章里出现过, 但是当时没感觉出其意义来, 原来源头是在这?

解决了计算了和存储问题, 还有一个训练不稳定的问题要解决.

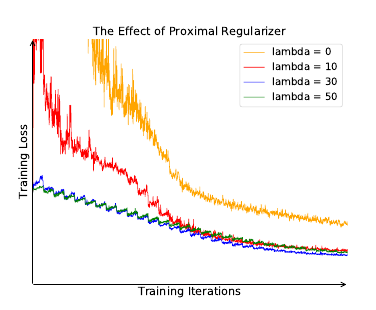
训练不稳定的诱因, 作者认为是每个样本作为一个类, 如此每个类在每个epoch里仅会被访问一次. 解决策略是用proximal 算子:

\[\mathcal{J}_{NCE}(\theta) = -\mathbb{E}_{P_d} [\log h(i, v^{(t-1)})-\lambda \|v^{(t)}-v^{(t-1)}\|] - m \cdot \mathbb{E}_{P_n}(\log (1 -h(i,v'))).
\]

有疑问的是, 我看的proximal算法里面, 应该是\(\log h(i, v^{(t)})\), 虽然二者可能相差不大.