A ROBUST KERNEL PCA ALGORITHM

目录

• 引
• 主要内容
  • 问题一
  • 问题二

Lu C, Zhang T, Du X, et al. A robust kernel PCA algorithm[C]. international conference on machine learning and cybernetics, 2004: 3084-3087.

引

这篇文章的思想很简单，如何将robust 和 kernel结合起来：找出异常值，将异常值排除，再进行kernel PCA。但是实际上，并非这么容易。

首先，论文抛出了俩个问题：

1.在原空间中为异常值的点，通过kernel隐式地被映射到高维空间后是否依旧是异常值；

2.如何判断该点是否为异常值。

主要内容

问题一

论文引了一篇文献来说明此问题，我没有去查阅：

当非线性映射\(\Phi(\cdot)\)为连续平滑（可微？）的函数是，数据的拓扑结构 不变。所以，一般的kernel应当是符合条件的。

问题二

论文圈定一个范围，先找到一个超球体，将所有的数据点都包裹进去的最小超球体，即：

\[\|\Phi(x_i) - c\| \le R^2
\]

其中\(c\)是球体的中心，假设\(c = \sum \limits_i \lambda_i^0 \Phi(x_i)\),那么\(\lambda_i^0\)将是下列方程的最优解（这个也是引入文献说明的，我也不打算深究）：



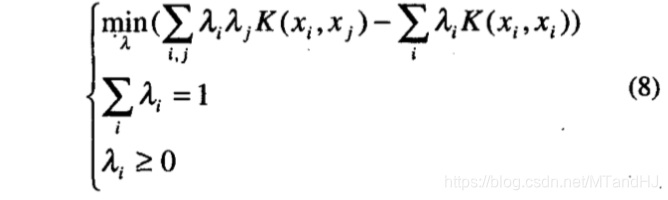
好吧，截个图：

有了中心，我们就可以通过计算\(\Phi(x_i)\)与\(c\)的最大距离来确定\(R\):



好了，现在\(R\)也找到了，可是，所有的点都在超球内，得找一个\(R'\)来限定出一些奇异值来，问题是\(R'\)该怎么找呢？这个地方我真的觉得蛮扯的，找一个\(R'\)使得异常点的数量为\(3\% \sim 5\%\)，这个怎么说呢，我觉得会不会太主观了。所以，就是以一定步长来搜索\(R'\)？感觉好蠢。