noip模拟6[辣鸡·模板·大佬·宝藏]

这怕不是学长出的题吧

这题就很迷

这第一题吧，正解竟然是O(n2)的，我这是快气死了，考场上一直觉得aaaaa n2过不了过不了，

我就去枚举边了，然后调了两个小时，愣是没调出来，然后交了个暴力，就走了15pts

然后我就淦第二题，这第一眼扫过去，就觉得是树链剖分，然后连复杂度都没算，就生生的码了一个小时，

给我弄傻了，好像复杂度是（8n+？？？？？nlogn）的，然后看了看最坏是（n²logn）的，不卡死你才怪！！！

然后这第三题吧，是这场考试中最让我后悔的一道题，看到概率期望就害怕，然后最后去干他，然后就没打完，然后还没思路

但是我总结到一个经验

有关有规律的随机数的问题，完全不需要考虑什么后效性，因为，是随机的，情况多去了

第四题，这是个非常非常狗的题，狗不狗先放一边，问题是他竟然是 李煜东蓝书上的原题，我没看到，但有人看过了。哇呜呜

还有一个事，这是我第一次在考场上用到对拍程序，还是有点小小的成就感的;

然后就是正解啦，这次改题非常顺利，没有浪费一丁点的时间

T1辣鸡

题目大意：给你张图，上面有好多为1的点，求这些点中，能够相邻并且利用对角线相连的边

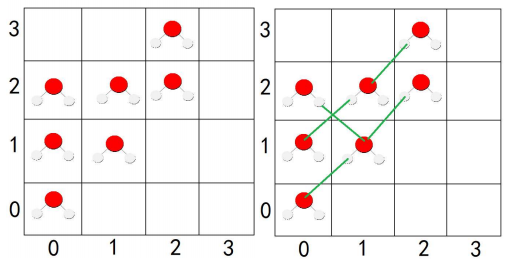就这样连接

然后这些点是通过一个一个小矩形给出来的，每次给出左下角和右上角的坐标，然后就可以计算了

第一眼看到这个题，我就直接蒙了一会，因为题面给了一个“曼哈顿距离”，就把我弄傻了

然后就打了个枚举点的极其暴力的打法，验证了我的猜想是正确的

然后我就开始想正解，显然我意识到了先算自己矩形内部的连边，再算两两矩形之间的连边

然后我想到了可以一个矩形一个矩形的枚举，然而，我在两秒钟之后就否掉了这个想法，因为，我认为复杂度太高了

可是苍天不公，这竟然是正解！！！！

首先枚举每个矩形内部的连边，O（1）计算  (y2-y1)*(x2-x1);

在枚举矩形之间的连边之前要先排序，按照x1升序,y1升序，排列

然后再枚举，注意这时候的各种判断就来了

自己推吧，主要注意判断两个矩形对角的时候，这个要单独判断，而且，不能与其他情况混起来算

然后先i-n  j=i+1~~n这样枚举，可以有减支的机会，如果向前枚举，那么只能不断continue，而不能break

这样时间就足以满足AC这道题了！！～～～

然后贴上代码，代码没有注释，自己看思路，然后理解代码，能不看就别就看

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define int long long
 4 #define re register int
 5 const int N=100005;
 6 struct node{
 7     int xa,xb,ya,yb;
 8     int zs,zx,ys,yx;
 9 }pos[N];
10 int n,ans;
11 bool com(node a,node b){
12     if(a.xa==b.xa)return a.ya<b.ya;
13     return a.xa<b.xa;
14 }
15 signed main(){
16     scanf("%lld",&n);
17     for(re i=1;i<=n;i++){
18         scanf("%lld%lld%lld%lld",&pos[i].xa,&pos[i].ya,&pos[i].xb,&pos[i].yb);
19     }
20     sort(pos+1,pos+n+1,com);
21     for(re i=1;i<=n;i++){
22         ans+=2*(pos[i].xb-pos[i].xa)*(pos[i].yb-pos[i].ya);
23         for(re j=i+1;j<=n;j++){
24             if(pos[j].xa-1>pos[i].xb)break;
25             if(pos[i].ya-1>pos[j].yb)continue;
26             if(pos[j].ya-1>pos[i].yb)continue;
27             if(pos[j].xa-1==pos[i].xb&&(pos[i].ya-1==pos[j].yb||pos[j].ya-1==pos[i].yb)){
28                 ans++;
29                 continue;
30             }
31             if(pos[j].xa-1==pos[i].xb){
32                 ans+=2*(min(pos[i].yb,pos[j].yb)-max(pos[i].ya,pos[j].ya));
33                 if(pos[i].ya!=pos[j].ya)ans++;
34                 if(pos[i].yb!=pos[j].yb)ans++;
35                 continue;
36             }
37             if(pos[j].ya-1==pos[i].yb||pos[i].ya-1==pos[j].yb){
38                 ans+=2*(min(pos[i].xb,pos[j].xb)-max(pos[i].xa,pos[j].xa));
39                 if(pos[i].xa!=pos[j].xa)ans++;
40                 if(pos[i].xb!=pos[j].xb)ans++;
41                 continue;
42             }
43         }
44     }
45     printf("%lld",ans);
46 }

T1

T2模板

题目大意：给你一棵树，每次任选一个节点，将这个节点到根的路径上都添加一个颜色，当然，每个点最多添加k[i]个颜色，最后让你统计，每个点的颜色种类数

我第一眼：卧槽！！

我第二眼：这不是链！！？？

我第三眼：剖分！！没的商量

然后我就风风火火的码了一个小时的树链剖分，然后信心满满的期待着满分，等来的却是0

对！他竟然管这题叫模板！！！怎么敢的

其实这个题的正解是线段树的启发式合并，其实也算是广义的线段树合并，因为他并没有直接去合并两颗线段树

而是不断的向其中一棵树插入另一棵树的节点，然后统计信息，因为这个题要统计的东西有点麻烦

既然每次向某一个节点插入颜色，那我们就先向这个节点插入，那么就“启发”你要向上合并了

好像我还想到了一点点正解，因为我读代码的时候不知道为什么要找到这个点的重儿子

后来才明白，因为这样的话可以尽量省去时间复杂度（这里的重儿子不是子树大小最大，而是子树中添加的颜色最多）时间就被省去好多

然后还要动态开点，因为这个空间复杂度实在是太高了，而且，对于每一次加颜色来说，只用到了线段树上的一条链，空间也大大优化了

还有就是统计颜色种类的问题

我们按照时间去建立一颗线段树，然后每个节点都要存放两个变量，颜色种类和所有颜色的数量

这样就符合了线段树的建立要求没可以进行上下转移，可以优化时间

同种颜色我们只能统计一次，按照常人的思路，都会去统计每种颜色第一次出现的时间，当然你要去统计最后一次也没人管你，就改个符号就好了

不对不对统计最后一次是不可以的，因为我们可以加的颜色数量是有限的，所以要统计第一次

然后每次合并的时候都把这个颜色的首次出现的时间更新;

这时候就和普通的线段树合并有不一样的了

普通的线段树合并，只是简单的将两颗子树的信息合并在一起，没有办法更新这颗树上原来最早的这个颜色的权值

所以我们带着要合并到的那个根去遍历另外一颗树，然后到了叶子节点，如果叶子节点存在，那就向我们带着的那个根中插入

在插入的过程中更新某种颜色的第一次出现的位置

这样就可以想普通线段树一样查询答案了;

代码（无注释）

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 #define re register int
  4 const int N=100005;
  5 int n,m;
  6 int to[N*2],nxt[N*2],head[N],rp;
  7 int k[N];
  8 struct node{
  9     int x,c;
 10 }dem[N];
 11 int lsh[N],lh;
 12 void add_edg(int x,int y){
 13     to[++rp]=y;
 14     nxt[rp]=head[x];
 15     head[x]=rp;
 16 }
 17 vector<int> mp[N];
 18 int rt[N];
 19 struct noda{
 20     int num[N*80],kin[N*80];
 21     int ls[N*80],rs[N*80];
 22     int seg;
 23     int pre[N],fro[N],tot;
 24     void pushup(int x){
 25         num[x]=num[ls[x]]+num[rs[x]];
 26         kin[x]=kin[ls[x]]+kin[rs[x]];
 27     }
 28     void ins(int &x,int l,int r,int pos,int ki,int nu){
 29         if(!x)x=++seg;
 30         if(l==r){
 31             kin[x]=ki;
 32             num[x]=nu;
 33             return ;
 34         }
 35         int mid=l+r>>1;
 36         if(pos<=mid) ins(ls[x],l,mid,pos,ki,nu);
 37         else ins(rs[x],mid+1,r,pos,ki,nu);
 38         pushup(x);
 39     }
 40     int query(int x,int l,int r,int siz){
 41         if(!x||!siz)return 0;
 42         if(l==r)return kin[x];
 43         int mid=l+r>>1,res=0;
 44         if(ls[x]&&siz<num[ls[x]])res+=query(ls[x],l,mid,siz);
 45         else{
 46             res+=kin[ls[x]];
 47             res+=query(rs[x],mid+1,r,siz-num[ls[x]]);
 48         }
 49         return res;
 50     }
 51     void cns(int x,int t,int co){
 52         if(!pre[co]){
 53             fro[++tot]=co;
 54             pre[co]=t;
 55             ins(rt[x],1,m,t,1,1);
 56             return ;
 57         }
 58         if(pre[co]<t){
 59             ins(rt[x],1,m,t,0,1);
 60             return ;
 61         }
 62         if(pre[co]>t){
 63             ins(rt[x],1,m,pre[co],0,1);
 64             ins(rt[x],1,m,t,1,1);
 65             pre[co]=t;
 66             return ;
 67         }
 68     }
 69     void merge(int x,int l,int r,int p){
 70         if(!x)return ;
 71         if(l==r){
 72             if(num[x])cns(p,l,dem[l].c);
 73             return ;
 74         }
 75         int mid=l+r>>1;
 76         merge(ls[x],l,mid,p);
 77         merge(rs[x],mid+1,r,p);
 78     }
 79     void cl(){
 80         while(tot)pre[fro[tot--]]=0;
 81     }
 82 }xds;
 83 int son[N],siz[N];
 84 int ans[N];
 85 void dfs1(int x,int f){
 86     siz[x]=mp[x].size()+1;
 87     for(re i=head[x];i;i=nxt[i]){
 88         int y=to[i];
 89         if(y==f)continue;
 90         dfs1(y,x);
 91         siz[x]+=siz[y];
 92         if(siz[y]>=siz[son[x]])son[x]=y;
 93     }
 94 }
 95 void dfs(int x,int f){
 96     //cout<<x<<" "<<"sb"<<endl;
 97     for(re i=head[x];i;i=nxt[i]){
 98         int y=to[i];
 99         if(y==f||y==son[x])continue;
100         dfs(y,x);xds.cl();
101     }
102     //cout<<"sb"<<endl;
103     if(son[x])dfs(son[x],x);
104     rt[x]=rt[son[x]];
105     for(re i=0;i<mp[x].size();i++)
106         xds.cns(x,mp[x][i],dem[mp[x][i]].c);
107     for(re i=head[x];i;i=nxt[i]){
108         int y=to[i];
109         if(y==f||y==son[x])continue;
110         xds.merge(rt[y],1,m,x);
111     }
112     ans[x]=xds.query(rt[x],1,m,k[x]);
113 }
114 signed main(){
115     scanf("%d",&n);
116     for(re i=1;i<n;i++){
117         int x,y;
118         scanf("%d%d",&x,&y);
119         add_edg(x,y);
120         add_edg(y,x);
121     }
122     for(re i=1;i<=n;i++)scanf("%d",&k[i]);
123     scanf("%d",&m);
124     for(re i=1;i<=m;i++){
125         scanf("%d%d",&dem[i].x,&dem[i].c);
126         lsh[i]=dem[i].c;
127     }
128     sort(lsh+1,lsh+m+1);
129     lh=unique(lsh+1,lsh+m+1)-lsh-1;
130     for(re i=1;i<=m;i++){
131         dem[i].c=lower_bound(lsh+1,lsh+lh+1,dem[i].c)-lsh;
132         mp[dem[i].x].push_back(i);
133     }
134     //cout<<"sb"<<endl;
135     dfs1(1,0);
136     dfs(1,0);
137     int q;
138     scanf("%d",&q);
139     for(re i=1;i<=q;i++){
140         int x;
141         scanf("%d",&x);
142         printf("%d\n",ans[x]);
143     }
144 }

T2

然后就是

T3大佬

题面：辣鸡ljh NOI之后就退役了，然后就滚去学文化课了。

他发现katarina大佬真是太强了，于是就学习了一下katarina大佬的做题方法。

比如这是一本有n道题的练习册，katarina大佬每天都会做k道题。

第一天做第1~k题，第二天做第 2~k+1

题……第n-k+1天做第n-k+1~n

道题。

但是辣鸡 ljh 又不想太累，所以他想知道katarina大佬做完这本练习册的劳累度。

每道题有它的难度值，假设今天katarina大佬做的题目中最大难度为t，那么今天katarina大佬的劳累度就是w[t]，做完这本书的劳累值就是每天的劳累值之和。

但是辣鸡ljh一道题都不会，自然也不知道题目有多难，他只知道题目的难度一定在1~m之间随机。

他想让即将参加 NOIP 的你帮他算算katarina大佬做完这本书的劳累值期望

这个题就很有意思，看上去哇塞，他好像有后效性诶，然后我就果断弃掉了，后来发现，以后不能随便放弃某个题

我们先只考虑考虑一天，每个题的难度取值都有m种可能性（先不考虑w）

那么最大值<=1的概率就是g[1]=(1/m)^k

　　　　　<=2的概率就是g[2]=(2/m)^k

　　　　　<=m的概率就是g[m]=1

这不相当于一个前缀和嘛，f[i]=g[i]-g[i-1]

然后我们就把概率求出来了，简单暴了，然后我们就可以直接拿概率*w[i]然后求和

然后再乘上一个(n-k+1)因为一共有这么多天

代码

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define re register int
 4 const int N=505;
 5 const int mod=1000000007;
 6 int n,m,k;
 7 int f[N],g[N],ink;
 8 int w[N],ans;
 9 int ksm(int x,int y){
10     int ret=1;
11     while(y){
12         if(y&1)ret=1ll*ret*x%mod;
13         x=1ll*x*x%mod;
14         y>>=1;
15     }
16     return ret;
17 }
18 signed main(){
19     scanf("%d%d%d",&n,&m,&k);
20     ink=ksm(ksm(m,k),mod-2);
21     for(re i=1;i<=m;i++){
22         g[i]=1ll*ksm(i,k)*ink%mod;
23         f[i]=(g[i]-g[i-1]+mod)%mod;
24         scanf("%d",&w[i]);
25         ans=(1ll*ans+1ll*w[i]*f[i]%mod)%mod;
26     }
27     if(k>n)ans=0;
28     ans=1ll*ans*(n-k+1)%mod;
29     printf("%d",ans);
30 }

T3

然后就

T4宝藏

一眼就看出来这个题是状压，然后就不知道该怎么办了

毕竟这么小的数据范围，我还能想到啥

好像这个题暴搜/模拟退火都能过诶

然后我还是老老实实的去状压，

设dp[i][s]为目前最大深度为i，已经可以达到的点的状态为s

然后就有一个转移方程f[i][j]=min(f[i-1][k]+cos(k,j)*(i-1);

还有一些需要预处理的东西，比如由k能否转移到j，比如转移的最小花费是多少;

还有这个题最坑的地方------有重边！！！！

还好我机智，加了一个判断

然后关于为什么可以直接乘（i-1）而不需要考虑其他深度小于（i-1）的点，

因为如果他乘上（i-2）可以造成最优解，那么他一定不会停留在i-2这个点，就会向前转移

所以不需要考虑这些东西

代码

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 //#define int long long
 4 #define re register int
 5 const int N=1005;
 6 const int S=(1<<12)+10;
 7 int n,m;
 8 int to[N*2],nxt[N*2],val[N*2],head[N],rp;
 9 int edg[15][15];
10 void add_edg(int x,int y,int z){
11     to[++rp]=y;
12     val[rp]=z;
13     nxt[rp]=head[x];
14     head[x]=rp;
15     if(edg[x][y]>z)edg[x][y]=z;
16 }
17 int dp[15][S],minn[S][15],can[S];
18 void getmin(){
19     int now[15],dre[15],dnt,cnt,x;
20     for(re i=1;i<(1<<n);++i){
21         dnt=cnt=0;can[i]=i;x=i;
22         for(re j=1;j<=n;++j)
23             if((i>>(j-1))&1)now[++cnt]=j;
24             else dre[++dnt]=j;
25         for(re j=1;j<=dnt;++j){
26             for(re k=1;k<=cnt;++k){
27                 if(edg[dre[j]][now[k]]!=0x3f3f3f3f){
28                     //if(edg[dre[j]][now[k]]>10000)cout<<edg[dre[j]][now[k]]<<endl;
29                     can[i]|=(1<<(dre[j]-1));
30                     minn[i][dre[j]]=min(minn[i][dre[j]],edg[dre[j]][now[k]]);
31                 }
32             }
33         }
34     }
35 }
36 int value(int x,int y){
37     //cout<<x<<" "<<y<<endl;
38     int z=(y^x),ret=0;
39     //cout<<z<<" "<<endl;
40     for(re i=1;i<=n;++i)
41         if((1<<(i-1))&z){
42             ret+=minn[x][i];
43             //cout<<minn[x][i]<<endl;
44         }
45     return ret;
46 }
47 signed main(){
48     scanf("%d%d",&n,&m);
49     memset(edg,0x3f,sizeof(edg));
50     memset(minn,0x3f,sizeof(minn));
51     for(re i=1;i<=m;++i){
52         int x,y,z;
53         scanf("%d%d%d",&x,&y,&z);
54         add_edg(x,y,z);
55         add_edg(y,x,z);
56         //cout<<edg[x][y]<<" "<<edg[y][x]<<endl;
57     }
58     //cout<<(5^1)<<endl;
59     getmin();
60     //cout<<can[1]<<endl;
61     memset(dp,0x3f,sizeof(dp));
62     for(re i=1;i<=n;++i)dp[1][(1<<(i-1))]=0;
63     int ans=dp[1][(1<<n)-1];
64     //cout<<0x3f3f3f3f<<endl;cout<<dp[1][0]<<endl;
65     for(re i=2;i<=n;++i){
66         for(re j=1;j<(1<<n);++j){
67             for(re k=1;k<(1<<n);++k){
68                 if((j&can[k])!=j)continue;
69                 if((k&j)!=k)continue;
70                 if(dp[i-1][k]==0x3f3f3f3f)continue;
71                 dp[i][j]=min(dp[i][j],dp[i-1][k]+value(k,j)*(i-1));
72             }
73         }
74         //cout<<ans<<endl;
75         ans=min(ans,dp[i][(1<<n)-1]);
76     }
77     printf("%d",ans);
78 }

T4