P7518 & 省选联考2021 宝石

这是一篇极其简单连像我这样省三参加不了省选的蒟蒻都能看懂的题解

前置知识： 倍增LCA  二分 栈 题意

---

PS：这是一篇完全面向初学者的题解，会非常细，大佬请无视

题目传送门

没有思路的时候， 我们往往可以从简单的情况下手， 比如一条链

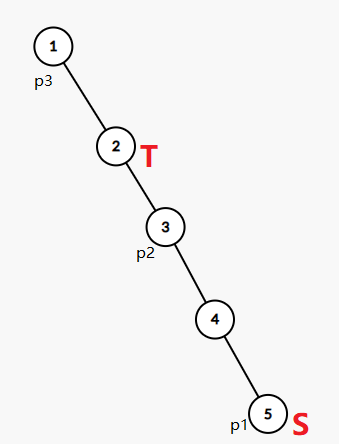
我们记Pi为第i个需要搜集的宝石， S为起点， T为终点。

不妨先假设我们有一条链， 每个节点指向下一个要搜集的宝石（向上）， 也就p1指向向上最近的一个p2， p2指向p3（为什么是最近，读者可自行思考）

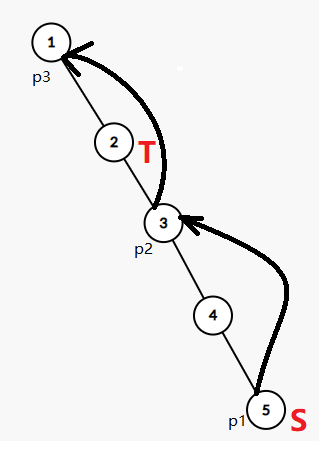
这个时候S是第一个要搜集的宝石, 我们考虑从S一路沿链往上跳，发现跳到1号点的时候就已经超过T了， 所以最多能跳到3号点， 也就是最多能搜集到P2

很简单， 链的情况我们已经解决了

然而这个算法的复杂度是O(n)的， 我们考虑优化。这时候，如果对lca十分熟悉的话， 就会想到在朴素lca中， 深度较大的那个节点会一直往上跳， 直到与另一个节点深度相同，与这个情况十分相同。

最后，lca采用倍增优化的方式往上跳

   for(int i=20;i>=0;i--)if(deep[f[x][i]]>=deep[y])x=f[x][i];

从大到小枚举， 如果深度没有超过另一个节点就往上跳

自然而然的想到，这道题也可以用倍增来跳， 预处理一个f数组， Fi, j 表示i号点， 下2^j个需要搜集的宝石的位置， 只要没有超过T就直接往上跳

for(int i=25; i>=0; i--){
    int next = f1[now][i];
    if(t!=0 && deep[next]>=deep[T]) now=next, i=25;
} 

好！链的情况解决链， 一般情况就很简单了。

（是不是讲的有点太细了

不难发现， S-T的路径被lca分成两部分。

对于S的那一部分，可以采用链的方法解决， 这时候我们得到一个Px：S链最远能匹配到的宝石，在上图中， x=2

对于T链， 我们并不能从lca往下跳（显然）， 我们考虑从下往上跳。

我们让p4指向p3（刚好相反）， 也就是让每个点指向上一个要搜集的宝石。

不妨从一个Py点开始向上跳， 假如能跳到一个Px+1， 那么Py就可以被搜集到（因为S已经从P1搜集到x了， T又从x+1搜集到y了，所以可以从1搜集到y）。

那么答案是不是可以搜集到y个呢？显然不是， 万一某个Pz也能够跳到Px+1， 而z>y呢

这时候仔细思考，答案有单调性，可以二分，（因为假如能从1搜集到z，肯定也能从1到y...）

所以最终的思路： 二分可以搜集到第几个颜色， 如果可以从该节点跳到x+1（倍增）， 则满足

复杂度

---

简单实现

　　实现很简单

　　1. 首先预处理三个倍增， 第一个普通倍增求LCA， 另外两个是S， T链上的倍增。

　　　　既然要倍增， 我们首先要知道每个节点的父节点，然后dp。对于这道题， 我们要知道对于某个点Px， 祖先中离他最近的Px+1， Px-1才行。怎么做呢？

　　　　很简单：对树进行dfs，开一个栈stack s[N]; 每到一个点Px就把节点编号压入s[x], 回溯的时候弹出就好了。所以 (S链）f1[x][0]=s[x+1].top(), (T) f2[x][0]=s[x-1].top();然后普通倍增就好了

for(int i=1; i<=n; i++){
        for(int j=1; j<=28; j++){
            f[i][j] = f[f[i][j-1]][j-1];
            f1[i][j] = f1[f1[i][j-1]][j-1];
            f2[i][j] = f2[f2[i][j-1]][j-1];
        }
    }

　　2.从S点找到最近的P1（s不一定是P1）， 然后往上跳， 求Px。这一步可以在上一步记录每一个节点最近的P1；

　  3.在T链二分能匹配第几个宝石， 对于每个Py, check的时候找到离T最近的Py往上跳（唉等等，这怎么找？总不能开个NM的数组在第一步记录吧？事实上可以离线来做， 再掉用一遍dfs， 搜索到某x点时，栈中就是每种颜色离x最近的 ，这个时候求出所有T为x的询问）

---

至于代码， 实现已经讲了就不放吧，没多长

其实是我tcl不想整理