P1721 [NOI2016] 国王饮水记题解

蒟蒻的第一篇黑题题解，求过。

题意描述

这道题用简洁的话来说，就是：

给你 $n$ 个数字，你可以让取其中任意若干个数字，每次操作，都会使所有取的数字变为取的数字的平均数，并且你最多只能进行 $k$ 次操作，你要在这经过最多 $k$ 次操作后使得给你的第一个数字变得最大。输出保留 $p$ 位的第一个数字的最后状态。

贪心策略（非正解，有助后面做题）

我们暂且不研究这道题的正解是什么，我们先看看怎么样贪心能够使得第一个数字变得最大。

首先，比第一个数字小的我们一定不需要，它们会使第一个数字变得更低
第二，我们需要知道求平均数的顺序，我们设三个水量， $h1,h2,h3(h1 <h2<h3)$ 。现在我们通过比较不同的顺序，看如何让 $h1$ 变得最大。

如图所示，已经是所有的顺序了：

$h1,h2,h3$ 同时求平均数。
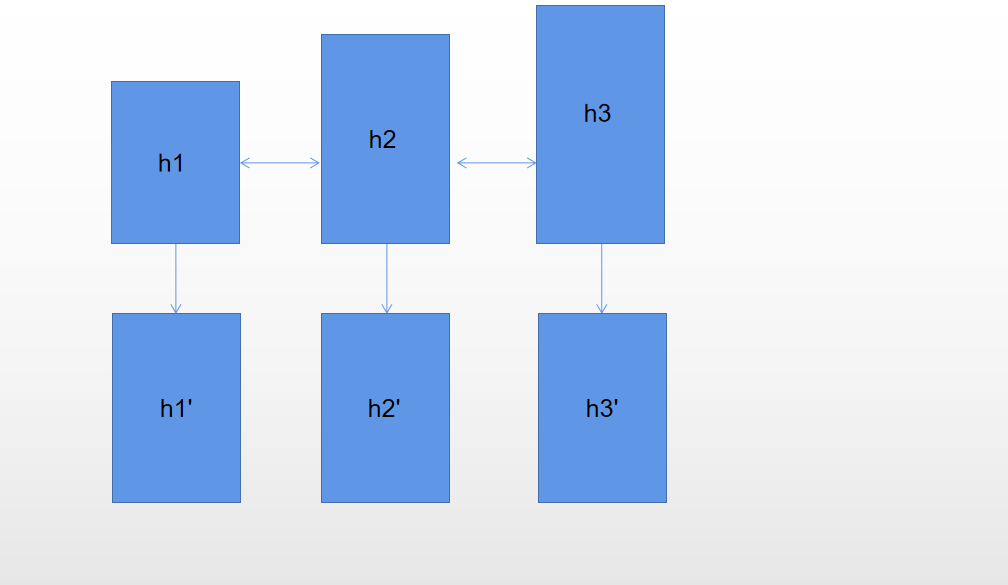
$h1$ 先和 $h3$ 求平均数，然后和 $h2$ 求平均数。
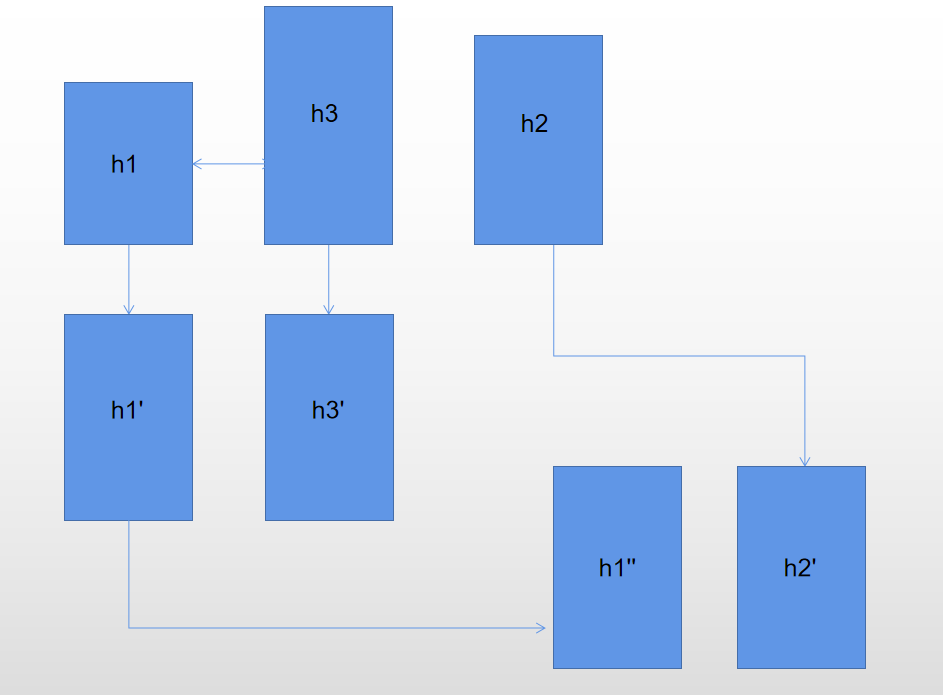
$h1$ 先和 $h2$ 求平均数，然后和 $h3$ 求平均数。

其实从图中就可以看出来，第三种方案最优。

我们再用数学的方法来比较这三个方案的优劣性。

第一种方案： $h1=(h1+h2+h3)/3$。
第二种方案： $h1=((h1+h3)/2+h2)/2=(h1+h3)/4+h2/2$。
第三种方案： $h1=((h1+h2)/2+h3)/2=(h1+h2)/4+h3/2$。

我们通过相减比较 $h1$ 最后的大小：

第一种方案减去第三种方案：

\[(h1+h2+h3)/3-(h1+h2)/4-h3/2
\]

\[\Longrightarrow (h1+h2)/3-(h1+h2)/4+h3/3-h3/2
\]

\[\Longrightarrow (4 \times h1+4 \times h2-3 \times h1-3 \times h2+4 \times h3-6 \times h3)/12
\]

\[\Longrightarrow (h1+h2-2 \times h3)/12
\]

\[\Longrightarrow ans<0
\]

第三种方案晋级。

第二种方案减去第三种方案：

\[(h1+h3)/4+h2/2-(h1+h2)/4-h3/2
\]

\[\Longrightarrow h1/4-h1/4+h2/2-h2/4+h3/4-h3/2
\]

\[\Longrightarrow (h2-h3)/2-(h2-h3)/4
\]

\[\Longrightarrow ans<0
\]

第三种方案胜出。

总结策略

只考虑比第一个数大的数。
在一般情况下，一个一个操作(可能会超过 $k$ 次，所以是在一般情况下)。
在一个一个操作时,从小到大操作。

斜率优化dp(正解)

由于可进行的操作次数是一定的，所以我们最后要解决的就是该在那一段区间进行操作。

首先将大于第一个数的数记录下来，排序并求出前缀和。

然后设计dp转移方程：

$sum_i$ 为前 $i$ 个数的前缀和(操作是赋值为平均数，并不会改变总数值，所以 $sum_i$ 一直适用) 。

$f_{i,j}$ 表示前面 $i$ 个数操作了 $j$ 次时第一个数的最大值。

得转移方程：

\[f_{i,j}=\max((f_{p,j-1}+sum_i-sum_{p-1})/(i-p+1))
\]

code

for(int j=1;j<=k;j++)

	for(int i=1;i<=n;i++)

		for(int p=1;p<i;p++)

			f[i][j]=max(f[i][j],(f[p][j-1]+sum[i]-sum[p-1])/(i-p+1));

但是这样的话，转移的时间复杂度为 $O(n^2kp)$ ，($n$ 是数字个数， $k$ 是操作次数,p为保留的精度）。

所以光是dp是不行的,我们要考虑优化dp。

我们观察这个状态转移方程：

\[(f_{p,j-1}+sum_i-sum_{p-1})/(i-p+1)
\]

\[\Longrightarrow (sum_i-(sum_{p-1}+f_{p,j-1}))/(i-(p-1))
\]

由于 $i$ 和 $j$ 是循环中给出的，所以我们将 $i$ 和 $j$ 提出：

\[\Longrightarrow (sum_{p-1}-f_p)/(p-1)
\]

经过前后对比，我们发现，设当前点为 $(i,sum_i)$ ,转移点为 $(p-1,sum_{p-1}-f_p)$ ，其实就是斜率公式。

用斜率优化dp，还有很重要的条件是要有单调性。如图，这道题目的单调性也十分的明显，由于 $1\le h_i \le 10^5$ ,也就意味着前缀和是单调上升的。

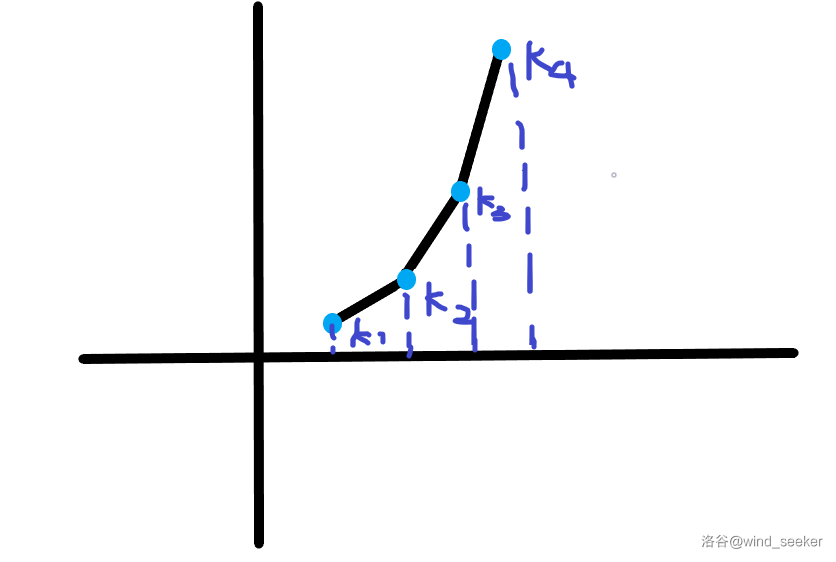
图画的不好，谅解。

那么我们要维护的就是图中的这一个凸包。

接下来我们考虑弹出队列的数会不会对后面的操作有影响：

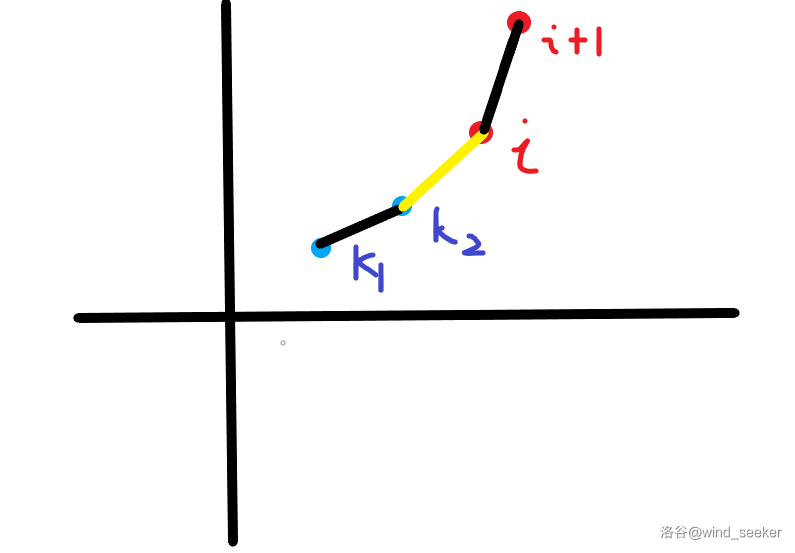
设当前位置为 $i$ ，对于 $i$ ,我们设 $k_2$ 优于 $k_1$ , 在这个情况下，我们可以得出：

\[(f_{k_1,j-1}+sum_i-sum_{k_1-1})/(i-k_1+1)<(f_{k_2,j-1}+sum_i-sum_{k_2-1})/(i-k_2+1)
\]

如果将 $i+1$ 带入,结果为：

\[(f_{k_1,j-1}+sum_{i+1}-sum_{k_1-1})/(i+1-k_1+1)<(f_{k_2,j-1}+sum_{i+1}-sum_{k_2-1})/(i+1-k_2+1)
\]

比较两个式子，我们会发现，在 $i+1$ 的情况下，如同 $i$ 的情况相同，原本优于 $k_1$ 的 $k_2$ 依然会比 $k_2$ 更优，所以弹掉 $k_1$ 并不会影响后面的操作。

code

for(int j=1;j<=k;j++)

{

	int head=tail=1;

	q[tail]=(node){1,sum[1]};

	for(int i=2;i<=n;i++)

	{

		node x=(node){i,sum[i]};

		while(head<tail&&slope(x,q[head])<slope(x,q[head+1]))head++;

		f[i][j]=(f[q[head]][j-1]+sum[i]-sum[q[head]-1])/(i-q[head]+1);

		while(head<tail&&slope(q[tail],q[tail-1])>slope(q[tail],i)) tail--;

		q[++tail]=i;

	}

}

此时我们已经将时间复杂度调小至 $O(nkp)$ 。

$n\le 8000\ \ k\le10^9\ \ p\le 3000$ 。

显然，我们还是不能过这道题目。

于是我们再次重审题目，看一下还有什么条件我们并没有用到。

Two thousands years later......

哦，我发，发现就怪了。

于是我参考了巨佬ljh2000的博客，终于发现了：$h_i$ 互不相同。 那么那么就意味着......

好吧......

于是我又一次参考了巨佬ljh2000的博客，里面有两条十分重要的性质：

每一次操作的区间长度一定不比上一次操作的区间长度长！
在所有水量高度互不相同的情况下，长度大于1的区间仅有 $O(\log{ \frac{nh}{H}})$ 个，其中 $H=\min(h_i-h_{i-1})$ 。

首先我们证明第一个，十分简单。我们的目标是将 $h_1$ 变得最大，而我们在一开始的时候对 $h_i$ 进行了排序，所以越往后面, $h_i$ 越大，越大的饼自然越要少与人分享，所以我们就会得出第一个结论。

至于第二个结论，我们只好根据众多大佬的指引，来到这里，深造一番。

Three thousands years later......

很好，没有任何的作用，看来只能等待某位大佬的指点，或者等本蒟蒻再深造几年再回答这个问题吧。

蒟蒻拙见，大佬勿喷。