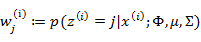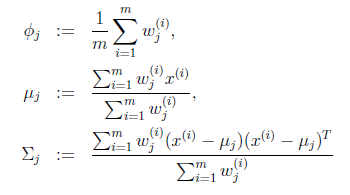混合高斯模型和EM算法
这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation)。
与k-means一样,给定的训练样本是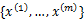 ,我们将隐含类别标签用
,我们将隐含类别标签用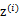 表示。与k-means的硬指定不同,我们首先认为
表示。与k-means的硬指定不同,我们首先认为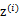 是满足一定的概率分布的,这里我们认为满足多项式分布,
是满足一定的概率分布的,这里我们认为满足多项式分布,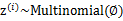 ,其中
,其中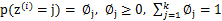 ,
,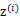 有k个值{1,…,k}可以选取。而且我们认为在给定
有k个值{1,…,k}可以选取。而且我们认为在给定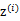 后,
后,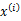 满足多值高斯分布,即
满足多值高斯分布,即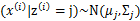 。由此可以得到联合分布
。由此可以得到联合分布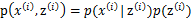 。
。
整个模型简单描述为对于每个样例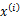 ,我们先从k个类别中按多项式分布抽取一个
,我们先从k个类别中按多项式分布抽取一个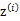 ,然后根据
,然后根据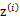 所对应的k个多值高斯分布中的一个生成样例
所对应的k个多值高斯分布中的一个生成样例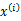 ,。整个过程称作混合高斯模型。注意的是这里的
,。整个过程称作混合高斯模型。注意的是这里的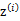 仍然是隐含随机变量。模型中还有三个变量
仍然是隐含随机变量。模型中还有三个变量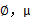 和
和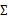 。最大似然估计为
。最大似然估计为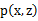 。对数化后如下:
。对数化后如下:
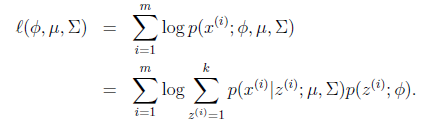
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的,因为求的结果不是close form。但是假设我们知道了每个样例的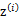 ,那么上式可以简化为:
,那么上式可以简化为:
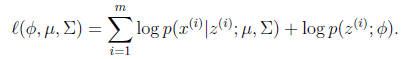
这时候我们再来对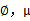 和
和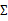 进行求导得到:
进行求导得到:
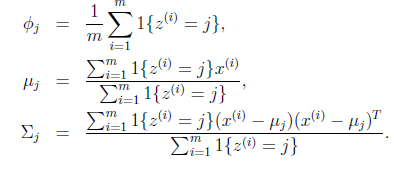
 就是样本类别中
就是样本类别中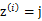 的比率。
的比率。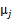 是类别为j的样本特征均值,
是类别为j的样本特征均值,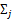 是类别为j的样例的特征的协方差矩阵。
是类别为j的样例的特征的协方差矩阵。
实际上,当知道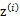 后,最大似然估计就近似于高斯判别分析模型(Gaussian discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
后,最大似然估计就近似于高斯判别分析模型(Gaussian discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
之前我们是假设给定了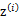 ,实际上
,实际上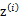 是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
|
循环下面步骤,直到收敛: { (E步)对于每一个i和j,计算
(M步),更新参数:
} |
在E步中,我们将其他参数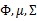 看作常量,计算
看作常量,计算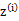 的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,
的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,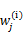 值又不对了,需要重新计算,周而复始,直至收敛。
值又不对了,需要重新计算,周而复始,直至收敛。
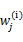 的具体计算公式如下:
的具体计算公式如下:
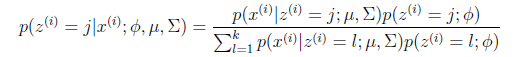
这个式子利用了贝叶斯公式。
这里我们使用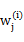 代替了前面的
代替了前面的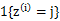 ,由简单的0/1值变成了概率值。
,由简单的0/1值变成了概率值。
对比K-means可以发现,这里使用了“软”指定,为每个样例分配的类别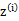 是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
虽然之前再K-means中定性描述了EM的收敛性,仍然没有定量地给出,还有一般化EM的推导过程仍然没有给出。下一篇着重介绍这些内容。
混合高斯模型和EM算法的更多相关文章
- 混合高斯模型和EM
<统计学习方法>这本书上写的太抽象,可参考这位大神的:http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html
- 高斯混合模型和EM算法
使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation). 与k-means一样,给定的训练样本是,我们将隐含类别标签用表示.与k- ...
- 最大熵模型和EM算法
一.极大似然已经发生的事件是独立重复事件,符合同一分布已经发生的时间是可能性(似然)的事件利用这两个假设,已经发生时间的联合密度值就最大,所以就可以求出总体分布f中参数θ 用极大似然进行机器学习有监督 ...
- 高斯混合模型的EM算法
高斯混合模型的EM算法 混合高斯模型 高斯混合模型的概率分布可以写成多个高斯分布的线形叠加,即 \[ p(\mathbf x) = \sum_{k=1}^{K}\pi_k\mathcal N(\mat ...
- SIGAI机器学习第二十三集 高斯混合模型与EM算法
讲授高斯混合模型的基本概念,训练算法面临的问题,EM算法的核心思想,算法的实现,实际应用. 大纲: 高斯混合模型简介实际例子训练算法面临的困难EM算法应用-视频背景建模总结 高斯混合模型简写GMM,期 ...
- 混合高斯模型的EM求解(Mixtures of Gaussians)及Python实现源代码
今天为大家带来混合高斯模型的EM推导求解过程. watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQveHVhbnl1YW5zZW4=/font/5a6L5L2T/ ...
- 机器学习之高斯混合模型及EM算法
第一部分: 这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation). 与k-means一样,给定的训练样本是,我们将隐含类 ...
- 机器学习基础知识笔记(一)-- 极大似然估计、高斯混合模型与EM算法
似然函数 常说的概率是指给定参数后,预测即将发生的事件的可能性.拿硬币这个例子来说,我们已知一枚均匀硬币的正反面概率分别是0.5,要预测抛两次硬币,硬币都朝上的概率: H代表Head,表示头朝上 p( ...
- 聚类之高斯混合模型与EM算法
一.高斯混合模型概述 1.公式 高斯混合模型是指具有如下形式的概率分布模型: 其中,αk≥0,且∑αk=1,是每一个高斯分布的权重.Ø(y|θk)是第k个高斯分布的概率密度,被称为第k个分模型,参数为 ...
随机推荐
- bootstrap-paginator 分页控件的使用
首先对js和css的引用 <link rel="stylesheet" href="reference/bootstrap/css/bootstrap.min.cs ...
- c++模板编程-typename与class关键字的区别
最近一直在研究c++模板编程,虽然有些困难,但希望能够坚持下去.今天,在书上看见一个讨论模板编程typename与class两个关键字的区别,觉得挺有意义的,就把它们给总结一下. 先看一个例子: te ...
- git merge –squash介绍
Git相对于CVS和SVN的一大好处就是merge非常方便,只要指出branch的名字就好了,如: $ git merge another $ git checkout another # modif ...
- 自定义栈类型,具有找到站内最小元素的min函数 ,且min(),pop(),push()函数的时间复杂度为O(1)
基本思想: // 借助一个辅助栈,入栈时,若新元素比辅助栈栈顶元素小,则直接放入辅助站 // 反之,辅助站中放入次小元素(即辅助栈栈顶元素)====保证最小元素出栈时,次小元素被保存 static c ...
- Google谷歌推出goo.gl缩短网址服务 - Blog透视镜
Blog部落格文章的网址,例如本篇文章:http://blog.openyu.org/2014/01/google-goo.gl.html,通常都很冗长,分享到社群网站上,容易使得讯息内容过多,同时也 ...
- ubuntu下查看IP Gateway DNS信息
使用nm-tool命令 在最底下有一行: IPv4 Settings: Address: 192.168.0.166 Prefix: (255.255.255.0) Gateway: 192.168. ...
- 【经验】在CSS中定义a:link、a:visited、a:hover、a:active顺序
摘自:http://www.qianyunlai.com/post-2.html 以前用CSS一直没有遇到过这个问题,在最近给一个本科同学做的项目里面.出现一些问题,搜索引擎查了一些网站和资料 ...
- 图片延迟加载scrollLoading.js应用
<ul> <li><a href="http://news.qq.com/" target="_b ...
- WIN8共享文件 详细设置
原文地址:http://jingyan.baidu.com/article/75ab0bcbff4274d6864db2f5.html win8共享文件设置 详细教程 | 浏览:6987 | 更新:2 ...
- Hdu4742-Pinball Game 3D(cdq分治+树状数组)
Problem Description RD is a smart boy and excel in pinball game. However, playing common 2D pinball ...