【集训笔记】贪心算法【HDOJ1052 【HDOJ2037

FatMouse' Trade

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 38780    Accepted Submission(s): 12797

Problem Description

FatMouse prepared M pounds of cat food, ready to trade with the cats guarding the warehouse containing his favorite food, JavaBean.
The warehouse has N rooms. The i-th room contains J[i] pounds of JavaBeans and requires F[i] pounds of cat food. FatMouse does not have to trade for all the JavaBeans in the room, instead, he may get J[i]* a% pounds of JavaBeans if he pays F[i]* a% pounds of cat food. Here a is a real number. Now he is assigning this homework to you: tell him the maximum amount of JavaBeans he can obtain.

 

Input

The input consists of multiple test cases. Each test case begins with a line containing two non-negative integers M and N. Then N lines follow, each contains two non-negative integers J[i] and F[i] respectively. The last test case is followed by two -1's. All integers are not greater than 1000.

 

Output

For each test case, print in a single line a real number accurate up to 3 decimal places, which is the maximum amount of JavaBeans that FatMouse can obtain.

 

Sample Input

5 3 7 2 4 3 5 2 20 3 25 18 24 15 15 10 -1 -1

 

Sample Output

13.333
31.500

解决这题的时候我如果按照单位量累加直到满足条件，会WA，可能是连double都存在精度损失吧

former:

 while(num < m){
            if(flag == n)
                break;
            if(a[flag].f ==){
                flag++;
            }else{
                    ans+=a[flag].di;
                    a[flag].f-=;
                    num++;
                }
        }
Later:

 #include<stdio.h>
 struct sc{
     int f,j;
     double di;
 }a[],temp;
 
 int main ()
 {
     int num,n,m,i,j,flag;
     double ans;
     while(scanf("%d%d",&m,&n)!=EOF){
         if(m==-&&n==-)
             break;
         ans=;
         num=;
         for(i=;i<n;i++){
             scanf("%d%d",&a[i].j,&a[i].f);
             a[i].di=(double)a[i].j/(double)a[i].f;
         }
         for(i=;i<n;i++){
             for(j=n-;j>=i;j--){
                 if(a[j].di > a[j-].di){
                     temp=a[j];a[j]=a[j-];a[j-]=temp;
                 }
             }
         }
 
         flag=;
         while(num < m){
             if(flag == n)
                 break;
 
             if(a[flag].f+num<= m){
                 ans+=a[flag].j;
                 num+=a[flag].f;
                 flag++;
             }
             else if(a[flag].f+num > m){
                 ans+=a[flag].di;
                 num++;
             }
         }
         printf("%.3lf\n",ans);
     }
     return ;
 }

HDOJ2037:(这也是一道上个学期A不了的题目)

今年暑假不AC

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 24701    Accepted Submission(s): 12935

Problem Description

“今年暑假不AC？”
“是的。”
“那你干什么呢？”
“看世界杯呀，笨蛋！”
“@#$%^&*%...”

确实如此，世界杯来了，球迷的节日也来了，估计很多ACMer也会抛开电脑，奔向电视了。
作为球迷，一定想看尽量多的完整的比赛，当然，作为新时代的好青年，你一定还会看一些其它的节目，比如新闻联播（永远不要忘记关心国家大事）、非常6+7、超级女生，以及王小丫的《开心辞典》等等，假设你已经知道了所有你喜欢看的电视节目的转播时间表，你会合理安排吗？（目标是能看尽量多的完整节目）

 

Input

输入数据包含多个测试实例，每个测试实例的第一行只有一个整数n(n<=100)，表示你喜欢看的节目的总数，然后是n行数据，每行包括两个数据Ti_s,Ti_e (1<=i<=n)，分别表示第i个节目的开始和结束时间，为了简化问题，每个时间都用一个正整数表示。n=0表示输入结束，不做处理。

 

Output

对于每个测试实例，输出能完整看到的电视节目的个数，每个测试实例的输出占一行。

 

Sample Input

12
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
0

 

Sample Output

5

 

解题思路即是按照每个节目的结束时间先从小到大排序

然后选择子窜的时候按照“最近结束时间”为标准

#include<stdio.h>
struct sc{
    int s,e;
}a[],tmp;
int main ()
{
    int i,j,t;
    int ti,now,ans;
    while(scanf("%d",&t)!=EOF){
        if(t==)
            break;
        for(i=;i<t;i++)
            scanf("%d%d",&a[i].s,&a[i].e);
        for(i=;i<t;i++){
            for(j=t-;j>=i;j--){
                if(a[j].e < a[j-].e){
                    tmp=a[j];a[j]=a[j-];a[j-]=tmp;
                }
            }
        }
        now=;
        ans=;
        int last,flag,min;
        while(){
            //printf("now s= %d e = %d\n",a[now].s,a[now].e);
            flag=;
            for(i=now+;i<t;i++){
                if(a[i].s >= a[now].e)
                    flag=;
            }
            if(!flag)
                break;
            last=;
            min=;
            for(i=now+;i<t;i++){
                //printf("%d \n",a[i].s - a[now].e );
                if(a[i].e - a[now].e < min && a[i].s - a[now].e >= ){
                    min=a[i].e - a[now].e;
                    last=i;
                }
            }
            if(min!=){
                ans++;
                now=last;
            }
        }
        printf("%d\n",ans);
    }
    return ;
}

TianJi—The Horse Racing

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10334    Accepted Submission(s): 2877

Problem Description

Here is a famous story in Chinese history.

"That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others."

"Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser."

"Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian's. As a result, each time the king takes six hundred silver dollars from Tian."

"Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match."

"It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king's regular, and his super beat the king's plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?"

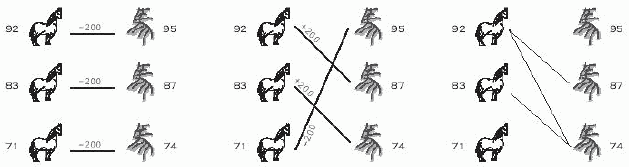
Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian's horses on one side, and the king's horses on the other. Whenever one of Tian's horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching...

However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses --- a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.

In this problem, you are asked to write a program to solve this special case of matching problem.

 

Input

The input consists of up to 50 test cases. Each case starts with a positive integer n (n <= 1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian’s horses. Then the next n integers on the third line are the speeds of the king’s horses. The input ends with a line that has a single 0 after the last test case.

 

Output

For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.

 

Sample Input

3

92 83 71

95 87 74

2

20 20

20 20

2

20 19

22 18

0

 

Sample Output

200

0

0

 

题意：田忌赛马。田忌和齐王各有n匹马，输入田忌的马的速度和齐王的马的速度。每一轮田忌赢了就得200两银子，平就得0两，输了就失去200两银子。问田忌最多能得到多少。题目的策略是贪心，分析见leokan大牛的blog，这里也转一下，留存根。

http://hi.baidu.com/leokan/blog/item/126da06e1dab5ade80cb4a4f.html

算法可以用DP，或者给每匹马连线赋权变为二分图最佳匹配，还有就是贪心了。
1.当田忌最慢的马比齐王最慢的马快，赢一场先
2.当田忌最慢的马比齐王最慢的马慢，和齐王最快的马比，输一场
3.当田忌最快的马比齐王最快的马快时，赢一场先。
4.当田忌最快的马比齐王最快的马慢时，拿最慢的马和齐王最快的马比，输一场。
5.当田忌最快的马和齐王最快的马相等时，拿最慢的马来和齐王最快的马比.

田忌赛马贪心的正确性证明。

先说简单状况下的证明：
1.当田忌最慢的马比齐王最慢的马快，赢一场先。因为始终要赢齐王最慢的马，不如用最没用的马来赢它。
2.当田忌最慢的马比齐王最慢的马慢，和齐王最快的马比，输一场。因为田忌最慢的马始终要输的，不如用它来消耗齐王最有用的马。
3.当田忌最慢的和齐王最慢的马慢相等时，分4和5讨论。
4.当田忌最快的马比齐王最快的马快时，赢一场先。因为最快的马的用途就是来赢别人快的马，别人慢的马什么马都能赢。
5.当田忌最快的马比齐王最快的马慢时，拿最慢的马和齐王最快的马比，输一场，因为反正要输一场，不如拿最没用的马输。
6.当田忌最快的马和齐王最快的马相等时，这就要展开讨论了,贪心方法是，拿最慢的马来和齐王最快的马比.
前面的证明像公理样的，大家一看都能认同的，没有异议的，就不细说了。

证明：田忌最快的马和齐王最快的马相等时拿最慢的马来和齐王最快的马比有最优解。

1）假设他们有n匹马，看n=2的时候.

a1 a2
b1 b2

因为 田忌最快的马和齐王最快的马相等 所以a1=b1,a2=b2 所以这种情况有2种比赛方式，易得这两种方式得分相等。

2）当数列a和数列b全部相等等时(a1=b1,a2=b2...an=bn)，显然最慢的马来和齐王最快的马比有最优解,可以赢n-1长，输1场，找不到更好的方

法了。
3）当数列a和数列b元素全部相等时(a1=b1=a2=b2...=an=bn)，无法赢也不输。

现在假设n匹马时拿最慢的马来和齐王最快的马比有最优解，证明有n+1匹马时拿最慢的马来和齐王最快的马比也有最优解。

数列
a1 a2 a3 a4...an an+1
b1 b2 b3 b4...bn bn+1

其中ai>=ai-1,bi>=bi-1

数列a和数列b不全部相等时，拿最慢的马来和齐王最快的马比数列得到数列
(a1) a2 a3 a4...an an+1
b1 b2 b3 b4...bn (bn+1)

分4种情况讨论 
1.b1=b2,an=an+1
则有
a2 a3 a4...an
b2 b3 b4...bn
其中a2>=a1,a1=b1,b1=b2,得a2>=b2(此后这种大小关系不再论述）,an>=bn.
此时若a2=b1,根据归纳假设，有最优解，否则a2>根据前面“公理”论证有最优解。
当且仅当a数列,b数列元素全部相等时有an+1=b1,已证得，所以an+1>b1，赢回最慢的马来和齐王最快的马比输的那一场。

2.b1<=b2,an=an+1
交换 b1,b2的位置，
数列
(a1) a2 a3 a4...an an+1
b2 b1 b3 b4...bn (bn+1)
此时 a2>=a1,an>=bn,
对于子表
a2 a3 a4...an
b1 b3 b4...bn
根据前面“公理”或归纳假设，有最优解。
an+1>=b2, 当且仅当b2=b3=b4=..=bn+1时有an+1=b2，这种情况，a中其它元素<=b1,b2,b3,b4..bn,对于这部分来说，能赢 x盘(x<=n)，假如不拿最慢的马来和齐王最快的马比则拿最快的马来和齐王最快的马比，此时平一盘，能赢x-1盘，而拿最慢的马来和齐王最快的马 比，输一盘能赢x盘，总的来说，还是X这个数，没有亏。

3.b1=b2,an<=an+1
4.b1<=b2,an<=an+1证明方法类似，不再重复。

以证得当有n+1匹马的时候，田忌和齐王最快最慢的马速度相等时，拿最慢的马来和齐王最快的马比有最优解，已知当n=2时成立，所以对于n>2且为整数（废话，马的只数当然是整数）时也成立。当n=1时....这个似乎不用讨论.

AC代码from(http://www.cnblogs.com/Action-/archive/2012/07/03/2574744.html):

#include <iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
 
bool cmp(int a,int b)
{
    return a>b;
}
 
int main()
{
    int n,money;
    int a[],b[];
    while(cin>>n)
    {
        if(!n)
            break;
        for(int i=;i<n;i++)
            cin>>a[i];
        for(int i=;i<n;i++)
            cin>>b[i];
        sort(a,a+n,cmp);
        sort(b,b+n,cmp);
        money=;
        for(int i=n-;i>=;i--)
        {
            if(a[i]>b[i])
            {
                money++;
            }
            else if(a[i]<b[i])
            {
                money--;
                for(int j=;j<i;j++)
                    b[j]=b[j+];
            }
            else if(a[i]==b[i])
            {
                if(a[]>b[])
                {
                    money++;
                    for(int j=;j<i;j++)
                    {
                        a[j]=a[j+];
                        b[j]=b[j+];
                    }
                }
                else if(a[]<b[])
                {
                    money--;
                    for(int j=;j<i;j++)
                        b[j]=b[j+];
                }
                else
                {
                    if(a[i]>b[])
                    {
                        money++;
                        for(int j=;j<i;j++)
                            b[j]=b[j+];
                    }
                    else if(a[i]<b[])
                    {
                        money--;
                        for(int j=;j<i;j++)
                            b[j]=b[j+];
                    }
                }
            }
        }
        cout<<money*<<endl;
    }
    return ;
}