长乐培训Day5

T1 圆圈舞蹈

题目

【题目描述】

熊大妈的奶牛在时针的带领下，围成了一个圈跳舞。由于没有严格的教育，奶牛们之间的间隔不一致。

奶牛想知道两只最远的奶牛到底隔了多远。奶牛A到B的距离为A顺时针走和逆时针走，到达B的较短路程。

告诉你相邻个奶牛间的距离，请你告诉奶牛两只最远的奶牛到底隔了多远。

【输入格式】

第一行一个整数N，表示有N只奶牛。

接下来2~N+1行，第I行有一个数，表示第I-1头奶牛顺时针到第I头奶牛的距离。

第N+1行的数表示第N头奶牛顺时针到第1头奶牛的距离。

【输出格式】

一行，表示最大距离。

【输入样例】

5

1

2

3

4

5

【输出样例】

7

【数据规模】

2<=N<=100000，

1<=距离<=maxlongint,距离和<=maxlongint。

解析

分析一下题目，多试几组数据，不难发现，其实我们并不需要知道所有牛之间的距离，

只需要知道对于每头牛来说，离它最远的牛有多远，实际实现时，我们需要求出每头牛顺时针与逆时针离它最远的牛。

这里引用一下大佬的解释：

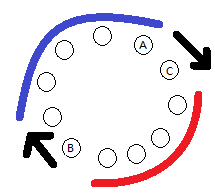
如图，对于枚举的第一头牛A，找到离它最远的牛B，

当我们沿顺时针枚举第二头牛C时，离C最远的牛不可能是图中红色区域的牛了，

所以我们只需要将B沿顺时针枚举，当蓝色部分的距离小于红色部分时枚举停止，

因为此时蓝色部分的牛不可能是离C最远的牛了。

这个算法是沿着圈绕了一圈，时间复杂度为O(n)，足以AC。

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = ;
int ans, a[MAXN], b[MAXN], n, i, j, k, tot, t;
int main()
{
    //freopen("circle.in", "r", stdin);
    //freopen("circle.out", "w", stdout);
    cin >> n;
    for(i = ; i <= n; i ++)
        scanf("%d", &a[i]);
    for(i = ; i <= n; i ++)
        tot += a[i];
    j = ;
    t = a[];
    for(i = ; i <= n; i ++)
    {
        while (min(t, tot - t) <= min(t + a[j], tot - t - a[j]) && j < n) j ++, t += a[j - ];
        ans = max(ans, min(t, tot - t));
        t -= a[i];
    }
    cout << ans << endl;
    //fclose(stdin); fclose(stdout);
}

T2 小麦亩产一千八

题目

【题目描述】

“有了金坷垃，肥料一袋能顶两袋撒，小麦亩产一千八，吸收两米下的氮磷钾……”，话说HYSBZ（Hengyang School for Boys & Zy）学识渊博孩纸们一讲到粮食，都会想起印度那个著名的故事：

国王要在第一个格子里放入一粒小麦，接下来的格子放入前面一个格子的两倍的小麦。这样所需小麦总数是巨大的，哪是不用金坷垃就能完成的任务？

不过为了减轻国王的任务，那个下棋获胜的宰相换了一个要求：“我只需要你在棋盘外放一粒小麦，可以将其理解为第0个格子，然后你需要在第一个格子里放入若干小麦，

之后每一个格子放入前两个格子的小麦数之和的小麦，并且要满足第a个格子放x粒小麦，第b个格子放……”说到这，宰相突然发现自己说的满足第a个格子放x粒小麦的情况可能不存在……

欺君可是大罪啊！国王看到宰相迟迟不说，自己也烦了！我自己来算！于是国王拜托你，让你算出第b个格子应该放几粒小麦。当然，就算答案不存在，你也是要告诉国王的。

【输入格式】

该题有多组数据，请读到文件末结束。

对于每一组数据仅一行，3个正整数a,x,b,分别表示第a个格子放了x粒小麦，以及你所需要计算的是第b个格子的小麦数量。

【输出格式】

对于每一次询问，仅1个整数，为第b个格子的小麦数量，若宰相说的情况不存在，那么请输出-1。

【输入样例】

1 1 2

3 5 4

3 4 6

12 17801 19

【输出样例】

2

8

-1

516847

【数据规模】

对于50%的数据：如果答案存在，那么p<=50

对于100%的数据：1<=数据组数<=10000，1<=a,b<=20, 数据保证如果答案存在，那么1<=p<=1000000.(注:p是第一格放置的小麦数)。

解析

题目明显给出了一个拓展的斐波那契数列，其满足：f[0]=1,f[1]=p,f[2]=p+1,f[3]=2*p+1······

而原来的斐波那契数列满足：F[0]=1,F[1]=1,F[2]=2,F[3]=3······

设g[i]=f[i]-F[i]，则g[0]=0,g[1]=p-1,g[2]=p-1,g[3]=2*p-2,g[4]=3*p-3······

输入已经给出了f[a]=x，所以g[a]=x-F[a]=F[a-1]*(p-1)，

我们先预处理出F数组，那么每组数据我们可以O（1）计算出p，

之后递推出答案就行了，每组数据时间复杂度为O（b）。

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int a, b;
long long f[], x;
inline void check(int mid)
{
    f[] = mid;
    for(int i = ; i <= a; i ++)
        f[i] = f[i - ] + f[i - ];
}
inline void getans(int mid)
{
    f[] = mid;
    for(int i = ; i <= b; i ++)
        f[i] = f[i - ] + f[i - ];
    printf("%lld\n", f[b]);
}
int main()
{
    //freopen("kela.in", "r", stdin);
    //freopen("kela.out", "w", stdout);return 0；
    f[] = ;
    while (scanf("%d%lld%d", &a, &x, &b) != EOF)
    {
        int l = , r = ;
        while (l != r - )
        {
            int mid = (l + r) >> ;
            check(mid);
            if (f[a] > x) r = mid;
            else l = mid;
        }
        check(l);
        if (f[a] == x) getans(l);
        else {
            check(r);
            if (f[a] == x) getans(r);
            else printf("-1\n");
        }
    }
    //fclose(stdin); fclose(stdout);
}

T3 好元素

题目

【题目描述】

小A一直认为，如果在一个由N个整数组成的数列{An}中，存在以下情况：

Am+An+Ap = Ai (1 <= m, n, p < i <= N ,  m,n,p可以相同)，那么Ai就是一个好元素。

现在小A有一个数列，请你计算数列中好元素的数目。

【输入格式】

第一行只有一个正整数N，意义如上。

第二行包含N个整数，表示数列{An}。

【输出格式】

输出一个整数，表示这个数列中好元素的个数。

【输入样例】

2

1 3

【输出样例】

1

【数据规模】

对于10%的数据1<=N<=10

对于40%的数据1<=N<=500 -10^5<=Ai<=10^5

对于70%的数据1<=N<=5000 -10^6<=Ai<=10^6

对于100%的数据1<=N<=5000 -10^9<=Ai<=10^9

解析

10分做法：四层循环枚举a[i],a[m],a[n],a[p]，时间复杂度O(n⁴)

40分做法：bool数组存储a[i]，再三层循环a[m],a[n],a[p]，若a[i]存在个数就+1，时间复杂度O(n³)

70分做法：我们发现40分做法计算三数和用了O(n³)，而查询a[i]只用了O(n)，

我们把代数式转换为a[m]+a[n]=a[i]-a[p]，这样计算和查询都是O(n²)，总时间复杂度为O(n²)

100分做法：在70分算法的前提下加上哈希进行判断即可。

Code

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<string>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<map>
#include<set>
using namespace std;

const int MAXN=int(5e3)+;
const int MAXH=int(1e7)+int(3e6);
const int Hash_Value=;
const int MAXV=Hash_Value+;

int Top,Val[MAXH],Next[MAXH],First[MAXV];
int N,Ans,A[MAXN];

void Push_Hash(const int &x) {
    int Px=x&Hash_Value;
    Next[++Top]=First[Px];
    Val[Top]=x;
    First[Px]=Top;
    return ;
}

bool Ask_Hash(const int &x) {
    int Px=x&Hash_Value;
    for (int k=First[Px];k!=;k=Next[k])
        if (Val[k]==x) return true;
    return false;
}

int Get() {
    int Sign=,Num=;
    char ch;
    for (ch=getchar();ch<''||ch>'';ch=getchar()) if (ch=='-') break;
    ch=='-'?Sign=:Num=ch-;
    for (ch=getchar();ch>=''&&ch<='';ch=getchar()) Num=Num*+ch-;
    return Sign==?Num:-Num;
}

int main() {
    //freopen("good.in","r",stdin);
    //freopen("good.out","w",stdout);
    N=Get();
    for (int i=;i<=N;++i) {
        A[i]=Get();
        for (int j=i-;j>=;--j) {
            int Now=A[i]-A[j];
            if (Ask_Hash(Now)) {
                ++Ans;
                break;
            }
        }
        for (int j=;j<=i;++j) {
            int Now=A[i]+A[j];
            Push_Hash(Now);
        }
    }
    printf("%d\n",Ans);
    //fclose(stdin);fclose(stdout);
    return ;
}

T4 国际象棋

题目

【题目描述】

小口口不是一个普通青年，所以他不喜欢玩普通国际象棋。他喜欢玩的国际象棋是这样的：把两个边长分别为 N*N 和 M*M 的国际象棋盘拼在一起。就像这样：

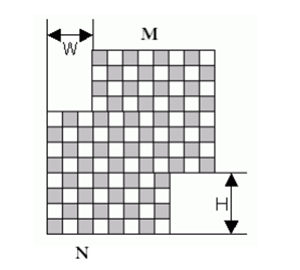
现在小口口又来刁难你了：他告诉你 N,M,W,H 以及 K。

然后问你这样的棋盘上放 K 个城堡互相不攻击有多少种方案。

城堡的攻击范围是一整行和一整列。

【输入格式】

第一行，五个整数，分别为 N,M,W,H,K。

【输出格式】

输出一行一个整数表示方案总数。

【输入样例】

8 8 3 4 1

【输出样例】

108

【数据规模】

10%的数据N=M=K.

50%的数据W=H=0,1<=N,M<=15(包括上述的10%的数据).

100%的数据N,M<=20,W,H,K<=10^9.

解析

本蒟蒻表示，这题神马不会写，随便写了个暴力就溜了。

So，直接抛出巨佬题解：

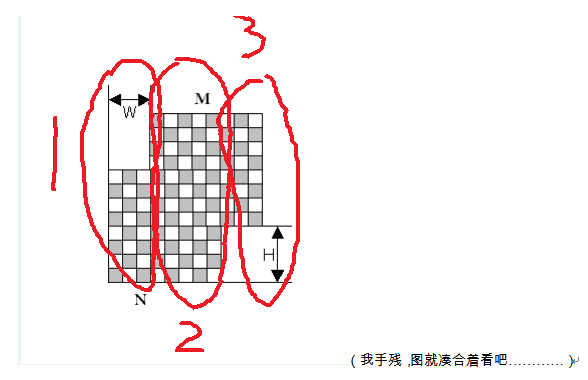
Code

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
int n,m,w,h,k,W,H;
struct ff {
    int len,a[];
    ff(){ len=; memset(a,,sizeof(a)); }

    inline ff operator *(const int &b){
        ff c=*this;
        for (int i=; i<=len; ++i) c.a[i]*=b;
        for (int i=; i<=len; ++i){
            c.a[i+]+=c.a[i]/;
            c.a[i]%=;
        }
        c.len=len;
        while (c.a[c.len+])
            c.len++, c.a[c.len+]=c.a[c.len]/, c.a[c.len]%=;
        return c;
    }
    inline void operator +=(const ff &b){
        len=max(len,b.len);
        for (int i=; i<=len; ++i){
            a[i]+=b.a[i];
            a[i+]+=a[i]/;
            a[i]%=;
        }
        while (a[len+]) ++len, a[len+]=a[len]/, a[len]%=;
    }
}f[][][][],ans;
void PRT(ff a)
{
    for (int i=a.len; i; --i)
        printf("%d",a.a[i]);
    printf("\n");
}
bool check(int x,int y)
{
    if (x<=n && y<=n) return ;
    if (x>w && x<=w+m && y>h && y<=h+m) return ;
    return ;
}
void work()
{
    if (w>=n) w=n;
    if (h>=n) h=n;
    if (m+w<=n && m+h<=n) w=h=,m=n;

    int H=max(h+m,n),W=max(m+w,n);                                        //H!W!
    int l1=w,l2=min(w+m,n),l3=max(w+m,n);
    int n1=l1,n2=l2-l1,n3=l3-l2;
    f[][][][].len=;
    f[][][][].a[]=;
    for (int i=; i<H; ++i){
        for (int x=; x<=n1; ++x)
        if (x<=k){
            for (int y=; y<=n2; ++y)
            if (x+y<=k)
              for (int z=; z<=n3; ++z)
              if (x+y+z<=k){
                    if (check(l1,i+)){
                        f[i+][x+][y][z]+=f[i][x][y][z]*(n1-x);
                    }
                    if (check(l3,i+)) f[i+][x][y][z+]+=f[i][x][y][z]*(n3-z);
                    if (check(l2,i+)) f[i+][x][y+][z]+=f[i][x][y][z]*(n2-y);
                    f[i+][x][y][z]+=f[i][x][y][z];
              }
        }
    }
    for (int x=; x<=n1; ++x)
      for (int y=; y<=n2; ++y)
        for (int z=; z<=n3; ++z)
        if (x+y+z==k){
           ans+=f[H][x][y][z];
        }
    for (int i=ans.len; i; --i)
        printf("%d",ans.a[i]);

}
int main()
{
    //freopen("chess.in","r",stdin);
    //freopen("chess.out","w",stdout);
    scanf("%d%d%d%d%d",&n,&m,&w,&h,&k);
    work();
    //fclose(stdin); fclose(stdout);
}