【数值分析】Python实现Lagrange插值

一直想把这几个插值公式用代码实现一下，今天闲着没事，尝试尝试。

先从最简单的拉格朗日插值开始！关于拉格朗日插值公式的基础知识就不赘述，百度上一搜一大堆。

基本思路是首先从文件读入给出的样本点，根据输入的插值次数和想要预测的点的x选择合适的样本点区间，最后计算基函数得到结果。直接看代码！（注：这里说样本点不是很准确，实在词穷找不到一个更好的描述。。。）

str2double

一个小问题就是怎样将python中的str类型转换成float类型，毕竟我们给出的样本点不一定总是整数，而且也需要做一些容错处理，比如多个+、多个-等等，也应该能识别为正确的数。所以实现了一个str2double方法。

import re
def str2double(str_num):
    pattern = re.compile(r'^((\+*)|(\-*))?(\d+)(.(\d+))?$')
    m = pattern.match(str_num)
    if m is None:
        return m
    else:
        sign = 1 if str_num[0] == '+' or '0' <= str_num[0] <= '9' else -1
        num = re.sub(r'(\++)|(\-+)', "", m.group(0))
        matchObj = re.match(r'^\d+$', num)
        if matchObj is not None:
            num = sign * int(matchObj.group(0))
        else:
            matchObj = re.match(r'^(\d+).(\d+)$', num)
            if matchObj is not None:
                integer = int(matchObj.group(1))
                fraction = int(matchObj.group(2)) * pow(10, -1*(len(matchObj.group(2))))
                num = sign * (integer + fraction)
        return num

我使用了正则表达式来实现，pattern = re.compile(r'^((\+*)|(\-*))?(\d+)(.(\d+))?$')可以匹配我上面提到的所有类型的整数和浮点数，之后进行匹配，匹配成功，如果是整数，直接return整数部分，这个用(int)强制转换即可；如果是浮点数，那么用(\d+)这个正则表达式再次匹配，分别得到整数部分和小数部分，整数部分的处理和上面类似，小数部分则用乘以pow(10, -小数位数)得到，之后直接相加即可。这里为了支持多个+或者-，使用re.sub方法将符号去掉，所以就需要用sign来记录数字的正负，在最后return时乘上sign即可。

binary_search

def binary_search(point_set, n, x):
    first = 0
    length = len(point_set)
    last = length
    while first < last:
        mid = (first + last) // 2
        if point_set[mid][0] < x:
            first = mid + 1
        elif point_set[mid][0] == x:
            return mid
        else:
            last = mid
    last =  last if last != length else last-1

    head = last - 1
    tail = last
    while n > 0:
        if head != -1:
            n -= 1
            head -= 1
        if tail != length:
            n -= 1
            tail += 1
    return [head+1, tail-1] if n == 0 else [head+1, tail-2]

这里point_set是全部样本点的集合，n是输入的插值次数，x是输入的预测点。返回合适的插值区间，即尽可能地把x包在里面。

因为要根据输入得到合适的插值区间，所以就涉及查找方面的知识。这里使用了二分查找，先对样本点集合point_set进行排序（升序），找到第一个大于需要预测点的样本点，在它的两侧扩展区间，直到满足插值次数要求。这里我的实现有些问题，可能会出现n=-1因为tail多加了一次，就在while循环外又进行了一次判断，n=-1时tail-2，这个实现的确不好，可能还会有bug。。。

最后，剩下的内容比较好理解，直接放上全部代码。

import re
import matplotlib.pyplot as plt
import numpy as np

def str2double(str_num):
    pattern = re.compile(r'^((\+*)|(\-*))?(\d+)(.(\d+))?$')
    m = pattern.match(str_num)
    if m is None:
        return m
    else:
        sign = 1 if str_num[0] == '+' or '0' <= str_num[0] <= '9' else -1
        num = re.sub(r'(\++)|(\-+)', "", m.group(0))
        matchObj = re.match(r'^\d+$', num)
        if matchObj is not None:
            num = sign * int(matchObj.group(0))
        else:
            matchObj = re.match(r'^(\d+).(\d+)$', num)
            if matchObj is not None:
                integer = int(matchObj.group(1))
                fraction = int(matchObj.group(2)) * pow(10, -1*(len(matchObj.group(2))))
                num = sign * (integer + fraction)
        return num

def preprocess():
    f = open("input.txt", "r")
    lines = f.readlines()
    lines = [line.strip('\n') for line in lines]
    point_set = list()
    for line in lines:
        point = list(filter(None, line.split(" ")))
        point = [str2double(pos) for pos in point]
        point_set.append(point)
    return point_set

def lagrangeFit(point_set, x):
    res = 0
    for i in range(len(point_set)):
        L = 1
        for j in range(len(point_set)):
            if i == j:
                continue
            else:
                L = L * (x - point_set[j][0]) / (point_set[i][0] - point_set[j][0])
        L = L * point_set[i][1]
        res += L
    return res

def showbasis(point_set):
    print("Lagrange Basis Function:\n")
    for i in range(len(point_set)):
        top = ""
        buttom = ""
        for j in range(len(point_set)):
            if i == j:
                continue
            else:
                top += "(x-{})".format(point_set[j][0])
                buttom += "({}-{})".format(point_set[i][0], point_set[j][0])
        print("Basis function{}:".format(i))
        print("\t\t{}".format(top))
        print("\t\t{}".format(buttom))

def binary_search(point_set, n, x):
    first = 0
    length = len(point_set)
    last = length
    while first < last:
        mid = (first + last) // 2
        if point_set[mid][0] < x:
            first = mid + 1
        elif point_set[mid][0] == x:
            return mid
        else:
            last = mid
    last =  last if last != length else last-1

    head = last - 1
    tail = last
    while n > 0:
        if head != -1:
            n -= 1
            head -= 1
        if tail != length:
            n -= 1
            tail += 1
    return [head+1, tail-1] if n == 0 else [head+1, tail-2]

if __name__ == '__main__':
    pred_x = input("Predict x:")
    pred_x = float(pred_x)
    n = input("Interpolation times:")
    n = int(n)
    point_set = preprocess()
    point_set = sorted(point_set, key=lambda a: a[0])
    span = binary_search(point_set, n+1, pred_x)
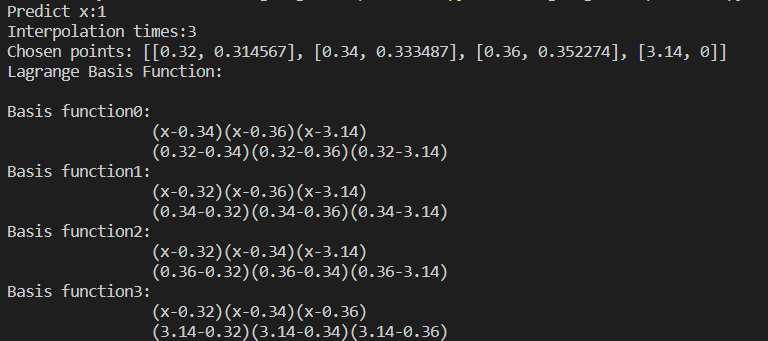
    print("Chosen points: {}".format(point_set[span[0]:span[1]+1]))
    showbasis(point_set[span[0]:span[1]+1])

    X = np.linspace(-np.pi, np.pi, 256, endpoint=True)
    S = np.sin(X)
    L = [lagrangeFit(point_set, x) for x in X]
    L1 = [lagrangeFit(point_set[span[0]:span[1]+1], x) for x in X]

    plt.figure(figsize=(8, 4))
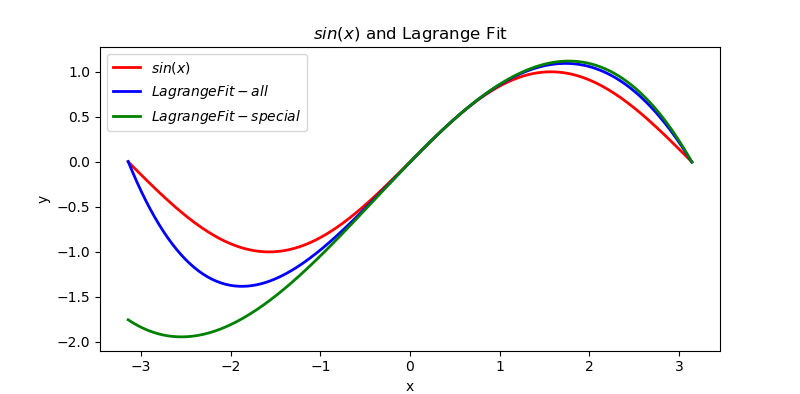
    plt.plot(X, S, label="$sin(x)$", color="red", linewidth=2)
    plt.plot(X, L, label="$LagrangeFit-all$", color="blue", linewidth=2)
    plt.plot(X, L1, label="$LagrangeFit-special$", color="green", linewidth=2)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.title("$sin(x)$ and Lagrange Fit")
    plt.legend()
    plt.show()

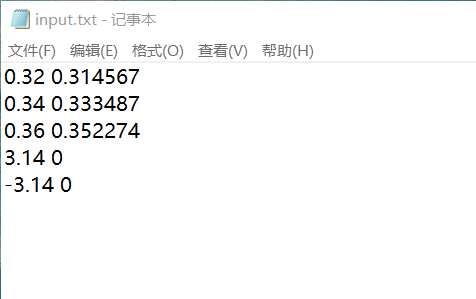
About Input

使用了input.txt进行样本点读入，每一行一个点，中间有一个空格。

结果

感觉挺好玩的hhh，过几天试试牛顿插值！掰掰！