P1801 黑匣子[堆]

题目描述

Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。

命令只有两种：

ADD(x):把x元素放进BlackBox;

GET:i加1，然后输出Blackhox中第i小的数。

记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：

我们来演示一下一个有11个命令的命令串。（如下图所示）

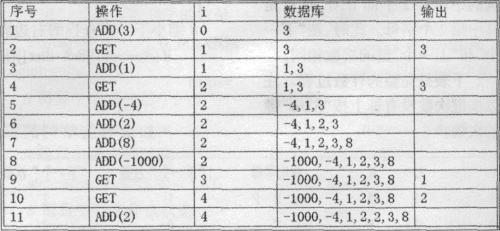
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：

1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。

2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。

解析

我一看，动态维护第k小，这不是对顶堆模板吗。

简单讲一下：对于一个递减的序列，长度为\(n\)，其中的值可以分为两部分：第\(1\sim k\)大的数为一部分，第\(k+1\sim n\)大数为第二部分 。对顶堆，就是用堆维护这两部分的数。我们不妨用一个大根堆维护\(1\sim k\)，用一个小根堆维护\(k+1\sim n\)，这样，第\(k\)小的数和第\(k+1\)小的数都恰好在堆顶，在输出时我们输出大根堆的堆顶就行了。这也是为什么这个方法叫对顶堆。

实现起来简单又快捷，优先队列就可以了。

参考代码

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#define ll long long
#define N 200010
using namespace std;
inline int read()
{
	int f=1,x=0;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
	return x*f;
}
priority_queue<ll> Q;
priority_queue<ll,vector<ll>,greater<ll> > q;
int k,a[N],b[N],n,m;
int main()
{
	m=read(),n=read();
	for(int i=1;i<=m;++i) a[i]=read();
	for(int j=1;j<=n;++j) b[j]=read();
	k=1;
	Q.push(a[1]);
	for(int i=1;i<=m;++i){
		if(i>1){
			if(a[i]>Q.top()) q.push(a[i]);
			else Q.push(a[i]);
		}
		while(i==b[k]){
			while(Q.size()>k) q.push(Q.top()),Q.pop();
			while(Q.size()<k) Q.push(q.top()),q.pop();
			++k,printf("%d\n",Q.top());
		}
	}
	return 0;
}