20101010 exam

2018 10.10 exam 解题报告

目录

• 2018 10.10 exam 解题报告
  • T1:LOJ #10078 新年好
    • 题目描述（原题来自：CQOI 2005）：
    • 输入格式:
    • 输出格式:
    • 样例输入：
    • 样例输出:
    • 数据范围与提示:
    • 思路：
    • 代码实现：
  • T2: LOJ #10220 Fibonacci 第 n 项
    • 题目描述
    • 输入格式
    • 输出格式
    • 样例输入
    • 样例输出
    • 数据范围与提示
    • 思路：
    • 代码实现：
  • T3: LOJ #10178 旅行问题
    • 题目描述
    • 输入格式
    • 输出格式
    • 样例输入
    • 样例输出
    • 数据范围与提示
    • 思路：
    • 代码实现：

T1:LOJ #10078 新年好

题目描述（原题来自：CQOI 2005）：

重庆城里有n个车站，m 条双向公路连接其中的某些车站。每两个车站最多用一条公路连接，从任何一个车站出发都可以经过一条或者多条公路到达其他车站，但不同的路径需要花费的时间可能不同。在一条路径上花费的时间等于路径上所有公路需要的时间之和。

佳佳的家在车站1，他有五个亲戚，分别住在车站 a,b,c,d,e。过年了，他需要从自己的家出发，拜访每个亲戚（顺序任意），给他们送去节日的祝福。怎样走，才需要最少的时间？

输入格式:

第一行：n,m为车站数目和公路的数目。

第二行：a,b,c,d,e为五个亲戚所在车站编号。

以下 m 行，每行三个整数 x,y,t，为公路连接的两个车站编号和时间。

输出格式:

输出仅一行，包含一个整数 T，为最少的总时间。

样例输入：

6 6

2 3 4 5 6

1 2 8

2 3 3

3 4 4

4 5 5

5 6 2

1 6 7

样例输出:

21

数据范围与提示:

对于全部数据，1≤n≤50000,1≤m≤1e5,1<a,b,c,d,e≤n,1≤x,y≤n,1≤t≤100.

思路：

对于考场上我咋想的。。。我已经不想说啥了，我个SB。。。本来想写单源最短路（dij+堆优化），，无奈，搞不出来，就写了个邻接表+spfa，虽然乱搞出样例，但是成功GG。

代码实现：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int N=5e4+10;
const int inf=0x7ffffff;

struct node{
	int v,nxt,val;
}e[N<<2];

int dis[7][N],a[10],head[N],f[50],Vis[N],vis[N];
int js,n,m,ans=inf;

inline int read() {
	int n=0,f=1;char ch=getchar();
	while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();}
	return n*f;
}

inline void add_edge(int u,int v,int val) {
	e[++js].v=v,e[js].val=val;
	e[js].nxt=head[u],head[u]=js;
} 

inline void spfa(int s,int t) {
	memset(vis,0,sizeof(vis));
	queue<int>q;
	q.push(s);
	vis[s]=1,dis[t][s]=0;
	while (!q.empty()) {
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i;i=e[i].nxt) {
			int v=e[i].v;
			if(dis[t][v]>dis[t][u]+e[i].val) {
				dis[t][v]=dis[t][u]+e[i].val;
				if(!vis[v]) {
					vis[v]=1;
					q.push(v);
				}
			}
		}
	}
}

inline void dfs(int t) {
	if(t==6) {
		int res=0;
		for(int i=1;i<6;++i) res+=dis[f[i]][a[f[i+1]]];
		ans=min(ans,res);
		return ;
	}
	for(int i=2;i<=6;++i) {
		if(!Vis[i]) {
			Vis[i]=1,f[t+1]=i;
			dfs(t+1),Vis[i]=0;
		}
	}
}

int main() {
	n=read(),m=read();
	for(int i=2;i<=6;++i) a[i]=read();
	for(int i=1;i<=m;++i) {
		int u=read(),v=read(),val=read();
		add_edge(u,v,val),add_edge(v,u,val);
	}
	memset(dis,0x3f,sizeof(dis));
	a[1]=f[1]=1;
	for(int i=1;i<=6;++i) spfa(a[i],i);
	dfs(1);
	printf("%d",ans);
	return 0;
}

T2: LOJ #10220 Fibonacci 第 n 项

题目描述

大家都知道 Fibonacci 数列吧，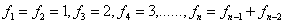

现在问题很简单，输入 n 和 m ，求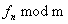

​

输入格式

输入 n,m。

输出格式

输出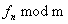

​

样例输入

5 1000

样例输出

5

数据范围与提示

对于 100% 的数据， 1≤n≤2×1e09,1≤m≤1e9+10.

思路：

直接上板子QWQ

代码实现：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

int n,m;

struct note{
	int a[2][2];
}e,a;

inline int read() {
	int n=0,f=1;char ch=getchar();
	while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();}
	return n*f;
}

inline void mul(note A,note &B) {
	note C;
	C.a[0][0]=C.a[0][1]=C.a[1][0]=C.a[1][1]=0;
	for(int i=0;i<=1;i++)
		for(int j=0;j<=1;j++)
			for(int k=0;k<=1;k++)
				C.a[i][j]=(1ll*A.a[i][k]*B.a[k][j]+1ll*C.a[i][j])%m;
	for(int i=0;i<=1;i++)
		for(int j=0;j<=1;j++)
			B.a[i][j]=C.a[i][j];
}

inline void gg(int y) {
	for(;y;y>>=1,mul(e,e))
	if(y&1) mul(e,a);
}

int main(){
	n=read(),m=read();
	a.a[0][0]=a.a[1][0]=1;e.a[0][0]=0,e.a[0][1]=e.a[1][0]=e.a[1][1]=1;
	if(n==1) printf("%d\n",1%m);
	gg(n-2);
	printf("%d",a.a[1][0]);
	return 0;
}

T3: LOJ #10178 旅行问题

题目描述

John 打算驾驶一辆汽车周游一个环形公路。公路上总共有 nnn 车站，每站都有若干升汽油（有的站可能油量为零），每升油可以让汽车行驶一千米。John 必须从某个车站出发，一直按顺时针（或逆时针）方向走遍所有的车站，并回到起点。在一开始的时候，汽车内油量为零，John 每到一个车站就把该站所有的油都带上（起点站亦是如此），行驶过程中不能出现没有油的情况。

任务：判断以每个车站为起点能否按条件成功周游一周。

​

输入格式

第一行是一个整数 n，表示环形公路上的车站数；

接下来 n 行，每行两个整数 p_i,d_i ，分别表示表示第 i 号车站的存油量和第 i 号车站到下一站的距离。

输出格式

输出共 n 行，如果从第 i 号车站出发，一直按顺时针（或逆时针）方向行驶，能够成功周游一圈，则在第 i 行输出 TAK，否则输出 NIE。

​

样例输入

5

3 1

1 2

5 2

0 1

5 4

样例输出

TAK

NIE

TAK

NIE

TAK

数据范围与提示

对于全部数据，3≤n≤1e6,0≤pi≤2×1e9,0<di≤2×1e9

思路：

DP ? QWQ,表示不造，咋办？模拟。。。完了后期模着模着，彻底凌乱了（qwq....我把自己写乱了），样例太水了，轻松水过，But...为毛一对拍就错了，好吧，于是就开始了花式乱搞之路，在偏离的道路上一去不复返...（调不出来，qaq，后期都没有动力了╮(╯▽╰)╭）

代码实现：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=2e6+10;
const int inf=0x7ffff;

inline int read() {
	int n=0,f=1;char ch=getchar();
	while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();}
	return n*f;
}

int n,m;
ll ans[N],pos[N],f[N],sum[N],p[N],d[N];

deque <int> q;

inline void check() {
	for(int i=1;i<=m;++i) sum[i]=sum[i-1]+f[i];
	for(int i=1;i<=m;++i){
		while(!q.empty() && sum[q.back()]>sum[i]) q.pop_back();
		q.push_back(i);
		while(q.front()<i-n+1) q.pop_front();
		if(i>=n && sum[q.front()]-sum[i-n]>=0) ans[pos[i-n+1]]|=1;
	}
}

int main() {
	n=read();
	m=n<<1;
	for(int i=1;i<=n;++i) p[i]=read(),d[i]=read();
	for(int i=1;i<=n;++i) f[i]=f[i+n]=p[i]-d[i],pos[i]=pos[i+n]=i;
	check();
	int js=1;
	f[js]=f[js+n]=p[1]-d[n];
	pos[js]=pos[js+n]=1;
	for(int i=n;i>=2;--i) {
		js++;
		f[js]=f[js+n]=p[i]-d[i-1];
		pos[js]=pos[js+n]=i;
	}
	check();
	for(int i=1;i<=n;++i) {
		if(ans[i]) printf("TAK\n");
		else printf("NIE\n");
	}
	return 0;
}