红黑树插入操作原理及java实现
红黑树是一种二叉平衡查找树,每个结点上有一个存储位来表示结点的颜色,可以是RED或BLACK。红黑树具有以下性质:
(1) 每个结点是红色或是黑色
(2) 根结点是黑色的
(3) 如果一个结点是红色的,则它的两个儿子都是黑色的
(4) 对于每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点
通过红黑树的性质,可以保证所有基于红黑树的实现都能保证操作的运行时间为对数级别(范围查找除外。它所需的额外时间和返回的键的数量成正比)。
Java的TreeMap就是通过红黑树实现的。
红黑树的操作如果不画图很容易搞糊涂,下面通过图示来说明红黑树的插入操作。
插入一个红色的节点到红黑树中之后,会有6种情况:图示中N表示插入的节点,P表示父节点,U表示叔叔节点,G表示祖父节点,X表示当前操作节点
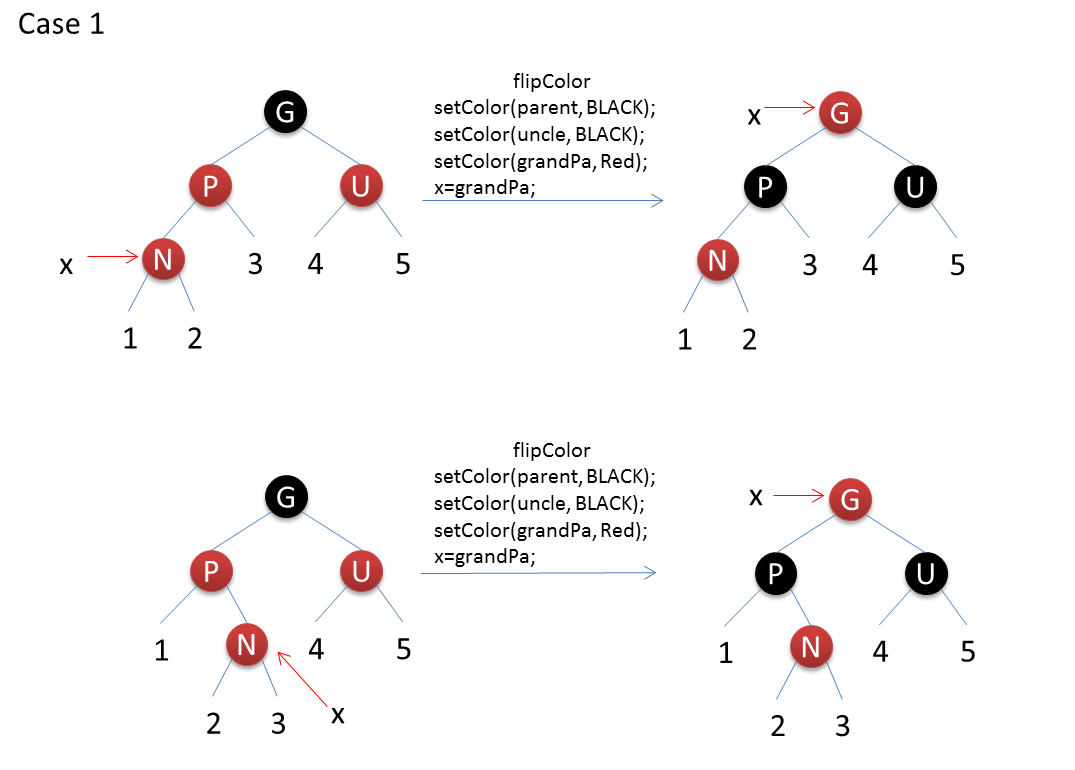

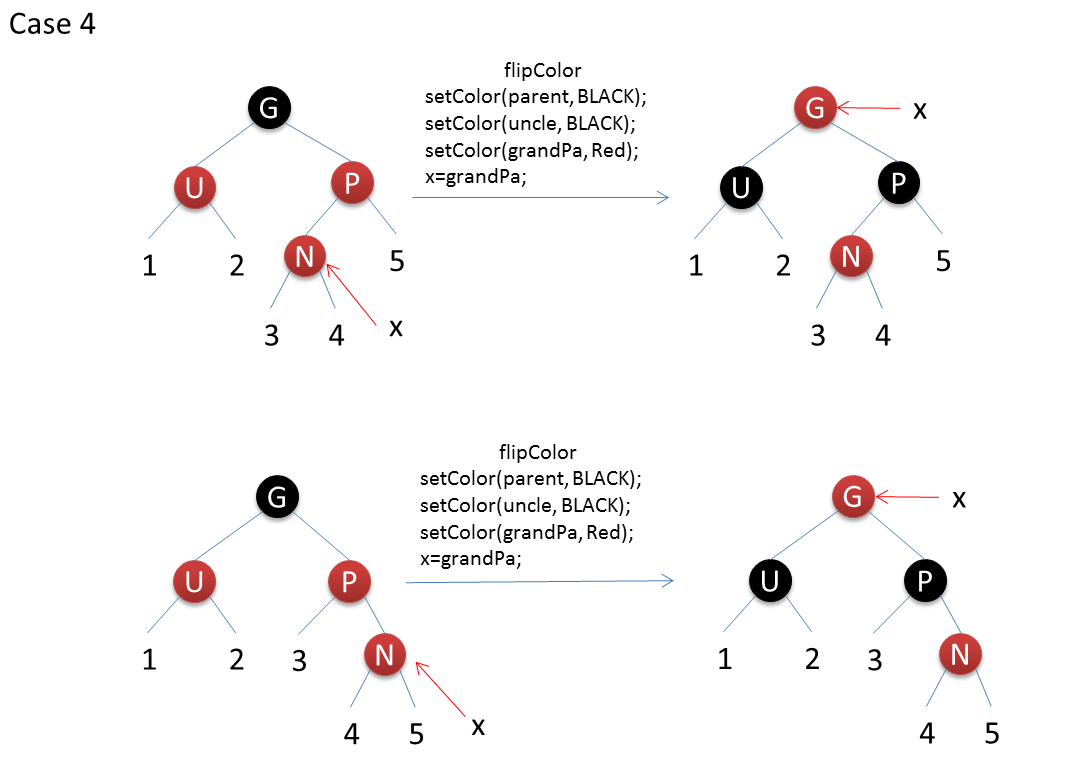
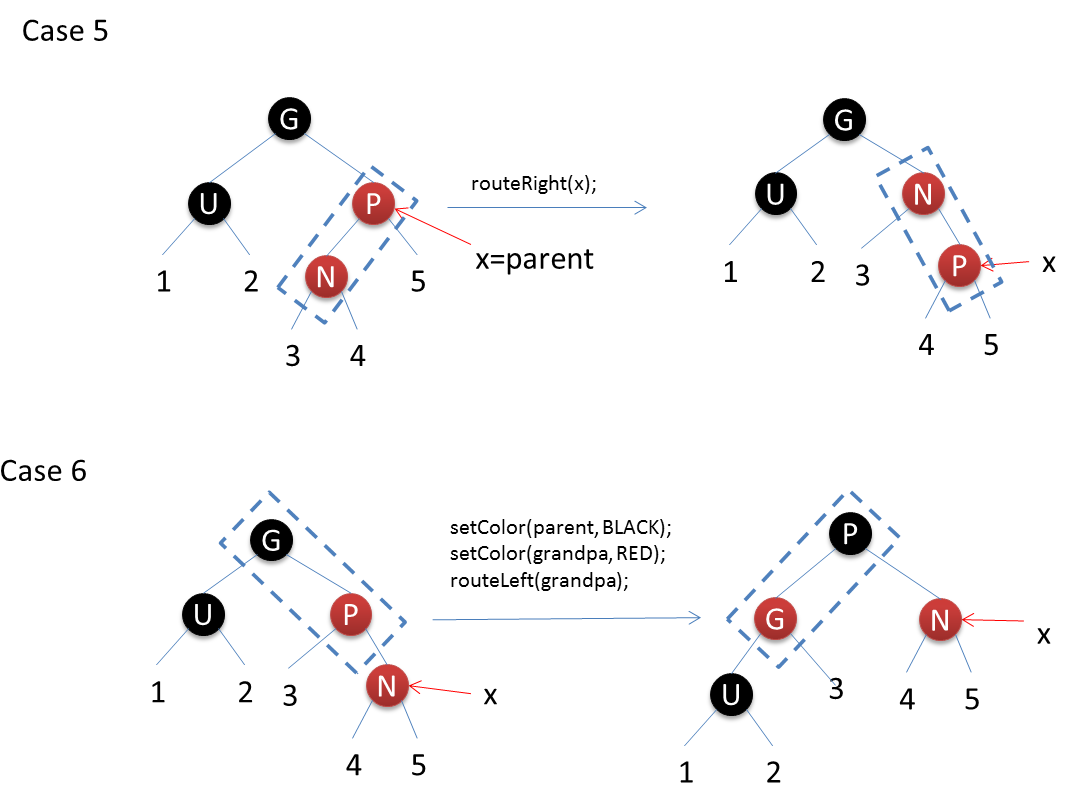
代码如下:
public class RedBlackBST<Key extends Comparable<Key>, Value> {
private Node root;
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
private Key key; //键
private Value val; //值
private Node left, right, parent; //左右子树和父节点
private boolean color; //由其父节点指向它的链接的颜色
public Node(Key key, Value val,Node parent, boolean color){
this.key = key;
this.val = val;
this.color = color;
}
}
public Value get(Key key){
Node x = root;
while(x!=null){
int cmp = key.compareTo(x.key);
if(cmp < 0 ) x = x.left;
else if(cmp > 0) x = x.right;
else return x.val;
}
return null;
}
public void put(Key key, Value val){
if(root==null) { //如果是根节点,就将节点新建为黑色
root = new Node(key,val,null,BLACK);
return;
}
//寻找合适的插入位置
Node parent = null;
Node cur = root;
while(cur!=null) {
parent = cur;
if(key.compareTo(cur.key)>0) cur=cur.right;
else cur = cur.left;
}
Node n = new Node(key,val,parent,RED); //普通的新建节点为红色
//将新节点插入parent下
if(key.compareTo(parent.key) > 0) parent.right = n;
else parent.left = n;
//插入新节点后要调整树中部分节点的颜色和属性来保证红黑树的特征不被破坏
fixAfterInsertion(n);
}
private Node parentOf(Node x) {
return (x==null ? null : x.parent);
}
private boolean colorOf(Node x) {
return (x==null ? BLACK : x.color);
}
private Node leftOf(Node x) {
return (x==null ? null : x.left);
}
private Node rightOf(Node x) {
return(x==null ? null : x.right);
}
private void setColor(Node x, boolean color) {
if(x!=null)
x.color = color;
}
private void fixAfterInsertion(Node x) {
while(x!=null && colorOf(parentOf(x)) == RED) {
Node grandPa = parentOf(parentOf(x));
Node parent = parentOf(x);
if(parent == leftOf(grandPa)) {//case 1 || case2 || case3
Node uncle = rightOf(grandPa);
if(colorOf(uncle) == RED) {//case1, uncle is red
setColor(parent,BLACK); //父节点置黑
setColor(uncle, BLACK); //叔叔节点置黑
setColor(grandPa,RED); //祖父节点置红
x = grandPa; //因为祖父节点由黑转红,故要重新调整父节点及其祖先的红黑属性
}else {//case2 || case3,uncle is black
if(x==rightOf(parent)) { //case2
x = parent;
rotateLeft(x);
}
//case3
setColor(parent,BLACK);
setColor(grandPa, RED);
rotateRight(grandPa);
}
}else {//case4 || case 5 || case6
Node uncle = leftOf(grandPa);
if(colorOf(uncle) == RED) { //case4 || case5 || case6
setColor(parent,BLACK);
setColor(uncle, BLACK);
setColor(grandPa,RED);
x = grandPa;
}else{ //case5 || case6, uncle is black
if(x==leftOf(parent)) { //case5
x = parent;
rotateRight(x);
}
//case6
setColor(parent,BLACK);
setColor(grandPa, RED);
rotateLeft(grandPa);
}
}
}
}
private void rotateLeft(Node x) {
if(x==null) return;
Node y = x.right;
x.right = y.left;
if(y.left!=null)
y.left.parent = x;
y.left = x;
y.parent = x.parent;
if(x.parent == null) {
root = y;
}
else if(x.parent.left == x) {
x.parent.left = y;
}else {
x.parent.right = y;
}
x.parent = y;
}
private void rotateRight(Node x) {
if(x==null) return;
Node y = x.left;
x.left = y.right;
if(y.right != null)
y.right.parent = x;
y.right = x;
y.parent = x.parent;
if(x.parent == null) {
root = y;
}else if(x.parent.left==x) {
x.parent.left = y;
}else {
x.parent.right=y;
}
x.parent = y;
}
}
上面的rotateLeft和rotateRight有必要画个图示:
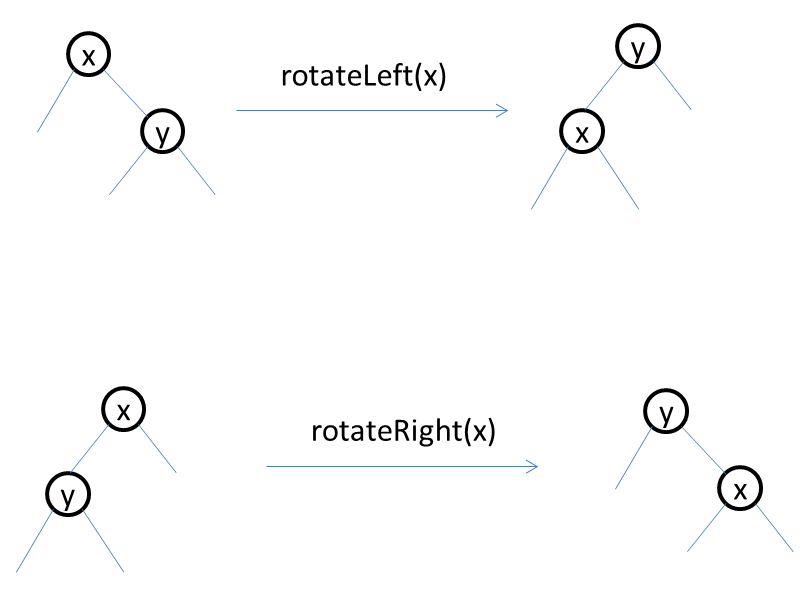
红黑树插入操作原理及java实现的更多相关文章
- stl map底层之红黑树插入步骤详解与代码实现
转载注明出处:http://blog.csdn.net/mxway/article/details/29216199 本篇文章并没有详细的讲解红黑树各方面的知识,只是以图形的方式对红黑树插入节点需要进 ...
- 红黑树深入剖析及Java实现
红黑树是平衡二叉查找树的一种.为了深入理解红黑树,我们需要从二叉查找树开始讲起. BST 二叉查找树(Binary Search Tree,简称BST)是一棵二叉树,它的左子节点的值比父节点的值要小, ...
- 红黑树插入与删除完整代码(dart语言实现)
之前分析了红黑树的删除,这里附上红黑树的完整版代码,包括查找.插入.删除等.删除后修复实现了两种算法,均比之前的更为简洁.一种是我自己的实现,代码非常简洁,行数更少:一种是Linux.Java等源码版 ...
- 红黑树深入剖析及Java实现(转自知乎美团点评技术团队)
作者:美团点评技术团队 链接:https://zhuanlan.zhihu.com/p/24367771 来源:知乎 著作权归作者所有.商业转载请联系作者获得授权,非商业转载请注明出处. 红黑树是平衡 ...
- 红黑树插入操作---以JDK 源码为例
红黑树遵循的条件: 1.根节点为黑色. 2.外部节点(叶子节点)为黑色. 3.红色节点的孩子节点为黑色.(由此,红色节点的父节点也必为黑色) 4.从根节点到任一外部节点的路径上,黑节点的数量相同. 节 ...
- jdk源码分析红黑树——插入篇
红黑树是自平衡的排序树,自平衡的优点是减少遍历的节点,所以效率会高.如果是非平衡的二叉树,当顺序或逆序插入的时候,查找动作很可能会遍历n个节点 红黑树的规则很容易理解,但是维护这个规则难. 一.规则 ...
- 红黑树(五)之 Java的实现
概要 前面分别介绍红黑树的理论知识.红黑树的C语言和C++的实现.本章介绍红黑树的Java实现,若读者对红黑树的理论知识不熟悉,建立先学习红黑树的理论知识,再来学习本章.还是那句老话,红黑树的C/C+ ...
- 基于Java实现红黑树的基本操作
首先,在阅读文章之前,我希望读者对二叉树有一定的了解,因为红黑树的本质就是一颗二叉树.所以本篇博客中不在将二叉树的增删查的基本操作了,需要了解的同学可以到我之前写的一篇关于二叉树基本操作的博客:htt ...
- 死磕 java集合之TreeMap源码分析(一)- 内含红黑树分析全过程
欢迎关注我的公众号"彤哥读源码",查看更多源码系列文章, 与彤哥一起畅游源码的海洋. 简介 TreeMap使用红黑树存储元素,可以保证元素按key值的大小进行遍历. 继承体系 Tr ...
随机推荐
- clock_gettime 用法
#include <stdio.h> #include <stdlib.h> #include <sys/types.h> #include <sys/sta ...
- Bullet:ORACLE Using SQL Plan Management(一)
SQL Plan Management如何工作? 当一个SQL硬解析时,基于成本的优化器CBO会生成多个执行计划,并从这些执行计划中选择一个优化器认为最低成本的执行计划. 如果SQL plan bas ...
- TFRecordReader "OutOfRangeError (see above for traceback): RandomShuffleQueue '_1_shuffle_batch/random_shuffle_queue' is closed and has insufficient elements (requested 1, current size 0)" 问题原因总结;
1. tf.decode_raw(features['image_raw'],tf.uint8) 解码时,数据类型有没有错?tf.float32 和tf.uint8有没有弄混??? 2. tf.tra ...
- HDU - 2044 - 一只小蜜蜂...(dp)
题意: 如题 思路: 仔细观察图 1-4和3-6其实是一样的答案,那么所有的方案都可以相减,意思为全部转化为从1开始 剩下的就是观察规律,仔细观察5号,能到5号蜂房的只有3和4,3和4到5号蜂房只有一 ...
- HDU - 5952 Counting Cliques(dfs搜索)
题目: A clique is a complete graph, in which there is an edge between every pair of the vertices. Give ...
- 55.fielddata内存控制以及circuit breaker断路器
课程大纲 fielddata加载 fielddata内存限制 监控fielddata内存使用 circuit breaker 一.fielddata加载 fielddata加载到内存的过程是lazy加 ...
- redis学习——数据类型
一.内容简介 Redis不仅仅是简单的key-value 存储器,同时也是一种data structures server.传统的key-value是指支持使用一个key字符串来索引value字符串的 ...
- c++ 上机实验题
c++语言俺是不会啦,但是朋友考试需要,那只能勉为其难的入门下做做考试题了. 以下就是具体的题目和答案: ----------------------------------------------- ...
- noip模拟赛 abcd
[问题描述]有4个长度为N的数组a,b,c,d.现在需要你选择N个数构成数组e,数组e满足a[i]≤e[i]≤b[i]以及 并且使得 最大.[输入格式]输入文件名为abcd.in.输入文件共 N+1 ...
- BZOJ2521 最小生成树 最小割
5.26 T2:最小生成树 Description Secsa最近对最小生成树问题特别感兴趣.他已经知道如果要去求出一个n个点.m条边的无向图的最小生成树有一个Krustal算法和另一个Prim的算法 ...
