hdu5698瞬间移动(组合数，逆元)

瞬间移动

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1422    Accepted Submission(s):
684

Problem Description

有一个无限大的矩形，初始时你在左上角（即第一行第一列），每次你都可以选择一个右下方格子，并瞬移过去（如从下图中的红色格子能直接瞬移到蓝色格子），求到第n

行第m

列的格子有几种方案，答案对1000000007

取模。

 

Input

多组测试数据。

两个整数n,m(2≤n,m≤100000)

 

Output

一个整数表示答案

 

Sample Input

4 5

 

Sample Output

10

 

Source

2016"百度之星"
- 初赛（Astar Round2B）

 

 

x和y分开考虑，在（1,1）到（n，m）之间可以选择走i步。就需要选i步对应的行C（n-2，i）及i步对应的列C（m-2，i）。相乘起来。 假设m<=n

 

 

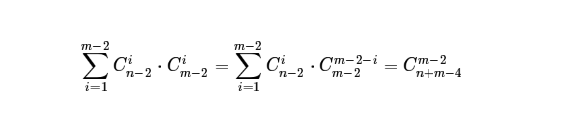
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 200001
#define M 1000000007
#define ll long long

using namespace std;
ll fac[N]={,},inv[N]={,},f[N]={,};
int n,m;

ll C(ll a,ll b)
{
    return fac[a]*inv[b]%M*inv[a-b]%M;
}

int main()
{
    for(int i=;i<N;i++)
    {
        fac[i]=fac[i-]*i%M;
        f[i]=(M-M/i)*f[M%i]%M;
        inv[i]=inv[i-]*f[i]%M;
    }
    while(~scanf("%d%d",&n,&m)) printf("%lld\n",C(m+n-,m-));
    return ;
}