【NOIP2016】DAY1 T2 天天爱跑步

Description

　　小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。?天天爱跑步?是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。

　　这个游戏的地图可以看作一一棵包含 N个结点和N-1 条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从1到N的连续正整数。

　　现在有个玩家,第个玩家的起点为Si ,终点为Ti 。每天打卡任务开始时,所有玩家在第0秒同时从自己的起点出发, 以每秒跑一条边的速度,不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)

　　小C想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。在结点的观察员会选择在第Wj秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第Wj秒也理到达了结点J 。小C想知道每个观察员会观察到多少人?

　　注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一段时间后再被观察员观察到。即对于把结点J作为终点的玩家: 若他在第Wj秒重到达终点,则在结点J的观察员不能观察到该玩家;若他正好在第Wj秒到达终点,则在结点的观察员可以观察到这个玩家。

Input

　　第一行有两个整数N和M 。其中N代表树的结点数量, 同时也是观察员的数量, M代表玩家的数量。

　　接下来n-1 行每行两个整数U和V ,表示结点U 到结点V 有一条边。

　　接下来一行N 个整数,其中第个整数为Wj , 表示结点出现观察员的时间。

　　接下来 M行,每行两个整数Si和Ti,表示一个玩家的起点和终点。

　　对于所有的数据,保证 1<=Si,Ti<=N,0<=Wj<=N。

Output

　　输出1行N 个整数,第个整数表示结点的观察员可以观察到多少人。

Sample Input

　6 3
　2 3
　1 2
　1 4
　4 5
　4 6
　0 2 5 1 2 3
　1 5
　1 3
　2 6

Sample Output

　2 0 0 1 1 1

HINT

对于1号点，W1=0，故只有起点为1号点的玩家才会被观察到，所以玩家1和玩家2被观察到，共2人被观察到。

对于2号点，没有玩家在第2秒时在此结点，共0人被观察到。

对于3号点，没有玩家在第5秒时在此结点，共0人被观察到。

对于4号点，玩家1被观察到，共1人被观察到。

对于5号点，玩家1被观察到，共1人被观察到。

对于6号点，玩家3被观察到，共1人被观察到。

Solution

这道题目吧，好难……

首先，我们读入的是一棵树，在某些结点上有一些玩家（废话，读过题的都知道）

那么对于某一个玩家，其实在树的某条链上有两种情况，一种是从下向上，另一种是从上向下，即该玩家还没走到起点和终点的lca，另一种已经过了起点和终点的lca（我废话真多）

我们先对于其中一种情况讨论，当该点从下向上时（我不会说是因为这种情况比较简单），如图P1，我们可以看出当且仅当w[i]+d[i]=d[x]时，从x出发的玩家才能被在i点的观察员观察到（d[i]表示结点i的深度），那么当该点从上向下时呢？我们看P2，显然当且仅当d[y]-d[i]=dis(x,y)-w[i]（dis(x,y)表示x与y之间的距离）我们把这个式子变形一下，w[i]-d[i]=dis(x,y)-d[y]（当然这个式子也可以写成w[i]-d[i]=d[x]-2*d[lca(x,y)]，因为dis(x,y)=d[x]+d[y]-2*d[lca(x,y)]）

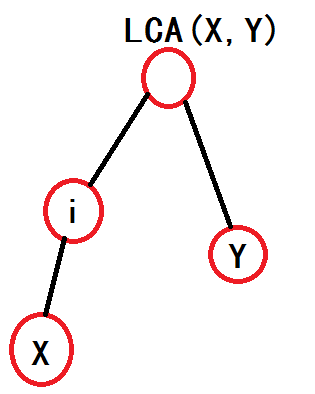
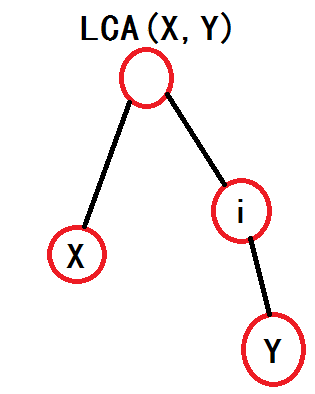
P1 P2

现在我们遇上了一个大问题，这两个式子如何来实现？

利用一个高档货，树上差分（不知道哪里高档，反正就是高档就对了），我们便可以在x上+1，在lca(x,y)上-1，对于y也相同，在y上+1，在lca(x,y)上-1，当我们对于这棵树dfs的时候，遍历到i时，利用差分就可以做到求出在i的子树中的能走到i的玩家数

可是我们要求的不仅仅是玩家经过该点，还需在同一时刻出现，其实我们只要做两个桶就可以了，桶p[k]记录起点的d[x]=k的玩家数量，桶q[k]记录终点的dis(x,y)-d[y]=k的玩家数量，对于每个点的答案就是q[d[i]+w[i]]+p[w[i]-d[i]]-这个点遍历前q[d[i]+w[i]]+p[w[i]-d[i]]（因为有些玩家从该点的祖先开始或结束但还没走到lca），当然我们需要记录以某个结点开始的玩家和以某个结束的玩家（这句话别看，因为我看了也懵，看下下面程序再结合一下这句话大概应该可能就可以看懂了吧）

还有一个小问题，就是当w[lca(x,y)]+d[lca(x,y)]==d[x]时，我们会发现向上走和向下走都会对lca有贡献，所以当lca可以观测到时我们需要把lca处的答案-1

但是还有一个坑，就是w[i]-d[i]可能小于0，那就把桶里面的数都加300000就可以了

讲得好水，看下程序吧（虽然说很丑）

 #include<cstdio>

 #include<utility>

 struct r{

     int to,last,w;

 }e[],in1[],ou1[],in2[],ou2[];

 int num=,num1=,num2=,num3=,num4=,head[],head1[],head2[],

     head3[],head4[],w[],d[],f[][],ans[];

 void add(int u,int v){

     e[num].to=v;

     e[num].last=head[u];

     head[u]=num++;

 }

 void add_edge(int u,r &p,int*q,int&num,int w){

     p.w=w;

     p.last=q[u];

     q[u]=num++;

 }

 inline int readin(){

     int c=getchar(),ret=;

     while (c<''||c>'') c=getchar();

     while (c>=''&&c<='') ret=(ret<<)+(ret<<)+c-'',c=getchar();

     return ret;

 }

 void dfs(int k,int fa){

     d[k]=d[fa]+;

     f[k][]=fa;

     for (int i=;i<=;i++) f[k][i]=f[f[k][i-]][i-];

     for (int i=head[k];i;i=e[i].last)if (e[i].to!=fa){

         dfs(e[i].to,k);

     }

 }

 int lca(int u,int v){

     if (d[u]>d[v]) std::swap(u,v);

     int y=d[v]-d[u];

     for (int i=;i>=;i--) if ((y&(<<i))) v=f[v][i];

     if (u==v) return u;

     for (int i=;i>=;i--) if (f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];

     return f[u][];

 }

 int q[],p[];

 void dfs2(int k,int fa){

     int req=q[d[k]+w[k]],rep=p[w[k]-d[k]+];

     for (int i=head1[k];i;i=in1[i].last) q[in1[i].w]++;

     for (int i=head3[k];i;i=in2[i].last) p[in2[i].w]++;

     for (int i=head[k];i;i=e[i].last) if (e[i].to!=fa) dfs2(e[i].to,k);

     ans[k]+=q[d[k]+w[k]]-req+p[w[k]-d[k]+]-rep;

     for (int i=head2[k];i;i=ou1[i].last) q[ou1[i].w]--;

     for (int i=head4[k];i;i=ou2[i].last) p[ou2[i].w]--;

 }

 int main()

 {

     int n=readin(),m=readin(),u,v,x,y;

     for (int i=;i<n;i++) u=readin(),v=readin(),add(u,v),add(v,u);

     num=;

     dfs(,);

     for (int i=;i<=n;i++) w[i]=readin();

     for (int i=;i<=m;i++){

         x=readin(),y=readin();

         int z=lca(x,y);

         if (d[x]==d[z]+w[z]) ans[z]--;

         add_edge(x,in1[num1],head1,num1,d[x]),

         add_edge(z,ou1[num2],head2,num2,d[x]),

         add_edge(y,in2[num3],head3,num3,d[x]-d[z]*+),

         add_edge(z,ou2[num4],head4,num4,d[x]-d[z]*+);

     }

     dfs2(,);

     for (int i=;i<=n;i++)

     printf("%d ",ans[i]);

     return ;

 }