【项目发起】千元组装一台大型3D打印机全教程（一）前言

前言

最近又碰到了大尺寸模型打样的需求，我这台17cm直径的kossel mini就捉襟见肘了。怎么办呢，这个时候kossel的好就体现出来了，随意扩展，那么就自己做个kossel-max吧。为了向前辈M大致敬，会全程直播草案的设计，配件的采购，主板的配置调试，组装，调平以及精度的调试，也给想做kossel的童鞋们另外一个选择。文中主要参考kossel原版，M大的kossel-mini改进项目和kossel-mini max项目。

下面是kossel mini 的视频（非广告，主要对没见过并联机的同谢对打印机有个概念）

项目参数

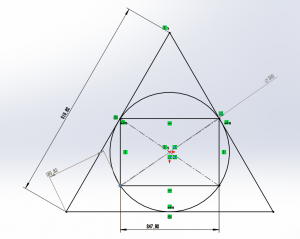
尺寸示意图

机身尺寸：三角形底座，边长~45cm，高度110cm，成型盘直径30cm

成型尺寸：底面Ø300MM，圆柱高度440MM，塔尖高度500MM

成型体积：31~32.5L（是kossel-mini标准版的近四倍，M大版本的近三倍）

耗材： Ø 1.75MM

大在哪里？为什么大的好？

是不是还在为放不下thinginverse里的plate而苦恼，很正常因为现在大部分plate都是20cm*20cm的尺寸来设计的，那么kossel能放下多大的呢？根据成型盘子的直径画了两个草图，如下图：

左图为kossel-mini 右图为kossel-max(草图中的巨型尺寸有误懒得改了，以下文中的尺寸为准)

标准的mini直径只有20cm，内切正方形边长=√（20*20/2）=14.1cm，更郁闷的是现在大部分的kosselmini在打印尺寸上都会比盘子要小（有的是因为外切三角形太小，就是框架的底座，有的是因为摇臂太短），一般20cm直径的盘子实际可打印直径只有17cm左右，那么内切正方形的边长就只剩下√（17*17/2)=12.02cm，不要哭，自己动手丰衣足食。

我们的max直径有30cm，三角边42cm，而臂长也达到36cm，所以不用考虑缩水的问题，内切正方形边长=√（30*30/2)=21.21cm，这下可以直接使用人家搭配好的盘子上菜了。

Kossel设计中高度一直是个头疼的问题，因为摇臂要浪费掉很多高度，而摇臂短了又会缩水，而mini版本中框架底部太小，一味增加高度很显然会不稳定，现在max的高度达到了1米，打印高度到了50cm也不会不稳，毕竟底座够大！而超高的高度给打印塔状模型带来了福音，是不是曾无数次败倒在艾菲尔铁塔下？原因无它，铁塔的筋实在太细了，而FDM就是不适合竖着打太细的东西，而在max下完全可以放大了再打，毫无压力。

3D打印机对比

3D打印技术又叫快速成型技术，已经发展了几十年了，我们说的FDM就是其中的热熔成型，也是现在价格最亲民的一种，机器大部分来源于开源组织reprap，最流行的分为下面几类

从左至右分别为Kossel,Ultimaker,Replicator,后两者最大的区别就是挤出机的位置

因为kossel没有螺杆驱动，所以速度是最快的，结构上也看得出kossel的性价比最高。

Kossel

优点：速度快，维护少，结构简单性价比高，校准快，调平方式简单；

缺点：塔状机身对稳定性要求高！

Ultimaker

优点：速度快和kossel差不多可以飙到300m+，稳定性高，调平方式一般；

缺点：调平比较麻烦，每次打印前都要校准，有的童鞋校准后无奈的用胶水来解决这个问题

Replicator 2X

优点：来自makerbot的设计，名气没得说，属于近程挤出，对各种模型适应性好，速度一般，稳定性高，调平同上；

缺点：较慢，升降个平台都要半分钟，调平问题同上；

Prusa i3

优点：超高的性价比，reprap的元老之一，也属于近程挤出，对各种模型适应性好，速度一般，稳定性一般，调平同上；

缺点：维护性差，虽然是第三代了还是同样的问题，调平问题同上；

超大Kossel Delta 3D Printer新闻

SeeMeCNC正在开工建设15英尺高的巨型kossel，这才叫真的大，打印真人大小的模型不在话下，不多说上图看就懂了。