k-svd字典学习，稀疏编码

1.     K-SVD usage:

Design/Learn a dictionary adaptively to betterfit the model and achieve sparse signal representations.

2.     Main Problem:

Y = DX

Where Y∈R(n*N), D∈R(n*K), X∈R(k*N), X is a sparse matrix.

3.    Objective function

4.       K-SVD的求解

Iterative solution: 求X的系数编码(MP/OMP/BP/FOCUSS),更新字典(Regression).

K-SVD优化：也是K-SVD与MOD的不同之处，字典的逐列更新：

假设系数X和字典D都是固定的，要更新字典的第k列d_k，领稀疏矩阵X中与d_k相乘的第k行记做，则目标函数可以重写为：

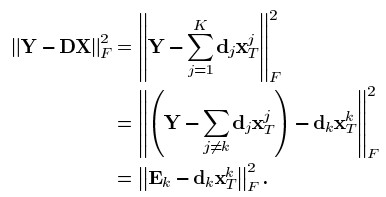
上式中，DX被分解为K个秩为1的矩阵的和，假设其中K-1项都是固定的，剩下的1列就是要处理更新的第k个。矩阵E_k表示去掉原子d_k的成分在所有N个样本中造成的误差。

5.       提取稀疏项

如果在4.中这一步就用SVD更新d_k和，SVD能找到距离E_k最近的秩为1的矩阵，但这样得到的系数不稀疏，换句话说，与更新d_k前的非零元所处位置和value不一样。那怎么办呢？直观地想，只保留系数中的非零值，再进行SVD分解就不会出现这种现象了。所以对E_k和做变换，中只保留x中非零位置的，E_k只保留d_k和中非零位置乘积后的那些项。形成，将做SVD分解，更新d_k。

6.       总结

K-SVD总可以保证误差单调下降或不变，但需要合理设置字典大小和稀疏度。

参考：http://blog.csdn.net/abcjennifer/article/details/8693342