[OS] 死锁相关知识点以及银行家算法详解

因此我们先来介绍一下死锁：

死锁特征

　　当出现死锁时，进程永远不能完成，并且系统资源被阻碍使用，阻止了其他作业开始执行。在讨论处理死锁问题的各种方法之前，先深入讨论一下死锁的特征。

·必要条件

（1）互斥：至少有一个资源必须处于非共享模式，即一次只有一个进程使用。如果另一进程申请该资源，那么申请进程必须等到该资源被释放为止。

（2）占有并等待：一个进程必须占有至少一个资源，并等待另一资源，而该资源为其他进程所占有。

（3）非抢占：资源不能被抢占，即资源只能在进程完成任务后自动释放。

（4）循环等待：有一组等待进程{P0，P1，···，Pn}，P0等待的资源为P1所占有，P1等待的资源为P2所占有，...，Pn-1等待的资源为Pn所占有，Pn等待的资源为P0所占有。

　　注：强调所有4个条件必须同时满足才会出现死锁。循环等待意味着占有并等待，这样四个条件并不完全独立。但是，在下面的讨论中我们会看到分开考虑这些条件是有意义的。

·资源分配图

　　死锁问题可用系统资源分配图的有向图进行更为精确的描述。这种图由一个结点集合V和一个边集合E组成。

　　由进程Pi到资源类型Rj的有向边记为Pi->Rj，称为申请边，它表示进程Pi已经申请了资源类型Rj的一个实例，并在等待该资源。由资源类型Rj到进程Pi的有向边记为Rj->Pi，称为分配边，它表示资源类型Rj的一个实例已经分配给进程Pi。

　　在图上，用圆形表示进程Pi，用矩形表示资源类型Rj。由于资源类型Rj可能有多个实例，所以在矩形中用圆点表示实例。注意申请边只指向矩形Rj，而分配边必须指定矩形内的某个圆点。

　　根据分配图的定义，可以证明：如果分配图没有环，那么系统就没有进程死锁，如果分配图有环，那么可能存在死锁。

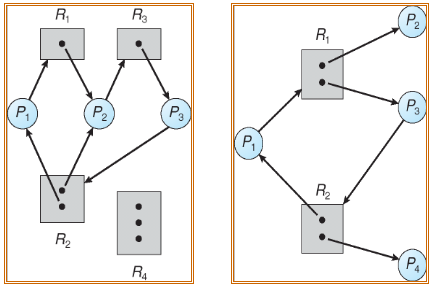
　　　存在死锁的资源分配图　　 存在环但没有死锁的资源分配图

由上图可知，资源分配图有环不一定会产生死锁。

死锁处理方法

·可使用协议以预防或避免死锁，确保系统不会进入死锁状态。

·可允许系统进入死锁状态，然后检测它，并加以恢复。

·可忽视这个问题，认为死锁不可能在系统内发生。

死锁预防

我们已经知道，出现死锁要满足4个必要条件，只要确保一个必要条件不成立，就能预防死锁发生。下面通过讨论这4个必要条件来研究死锁预防方法。

互斥：共享资源不是必须的，而非共享资源必须保持互斥
占有并等待：必须保证进程申请资源的时候没有占有其他资源
　　·要求进程在执行前一次申请全部的资源，只有没有占有资源时才可以分配资源
　　·利用率低，可能出现饥饿
非抢占：如果一个进程的申请没有实现，它要释放所有占有的资源
循环等待：将所有的资源类型放入资源列表中，并且要求进程按照资源表中递增的顺序申请资源

死锁避免

　　上面我们讨论的死锁预防算法中，通过限制资源申请的方法来预防思索。这种限制确保4个必要条件之一不会发生，因此死锁不成立。然而，通过这种方法预防死锁的副作用是低设备使用率和系统吞吐率。

·安全状态

　　系统安全指存在一个执行序列,所有进程都能完成，这个序列被称为安全序列。下面来举一个例子：

系统有三个进程P1、P2和P3，共有12台打印机。
进程P1总共要求10台打印机，P2和P3分别要求4台和9台
假定T0时刻，进程P1、P2和P3已分别获得5台、2台和2台，尚有3台空闲未分，如下表：

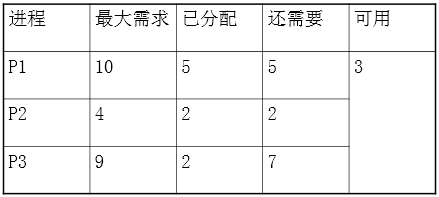
可以看出，存在一个安全序列P2、P1、P3，所以说T0时刻是系统安全的。

　　安全状态不是死锁状态。相反，死锁状态是不安全状态。然而，不是所有不安全状态都能导致死锁状态。不安全状态可能导致死锁。系统可以从安全状态转换为不安全状态。

　　有了安全状态的概念，可定义避免算法以确保系统不会死锁。其思想是简单地确保系统始终处于安全状态。开始，系统处于安全状态。当进程申请一个可用的资源时，系统必须确定这一资源申请是可以立即分配还是等待。只有分配后使系统仍处于安全状态，才允许申请。

　　采用这种方案，如果进程申请一个现已可用的资源，那么它可能必须等待。因此，与没有采用死锁避免算法相比，这种情况下资源使用率可能更低。

·资源分配图算法（适用于每种资源类型只有一个实例）

　　该算法是在资源分配图的基础上，引入一新类型的边，称为需求边。需求边Pi->Rj表示进程Pi可能在将来某个时候申请资源Rj。这种边类似于同一方向的申请边，但用虚线表示。当申请资源时，需求边变为申请边；释放资源时，申请边变为需求边。

　　假设进程Pi申请资源Rj。只有在将申请边Pi->Rj变为分配边Rj->Pi而不会导致资源分配图形成环时，才允许申请。

·银行家算法（适用于每种资源类型有多个实例）

为了实现银行家算法，必须要有几个数据结构：

注：设n为系统进程的个数，m为在资源类型的种类。

Available：长度为m的向量。表示每种资源的现有实例的数量。如果Available[j]=k，那么资源Rj有k个实例有效。

Max：n * m矩阵。定义每种进程的最大需求。如果Max[i][j]=k,那么进程Pi可以最多请求资源Rj的k个实例。

Allocation：n * m矩阵。定义每个进程现在所分配的各种资源类型的实例数量。如果Allocation[I,j]=k,那么进程Pj当前分配了k个资源Rj的实例。

Need：n * m矩阵。表示每个进程还需要的剩余的资源。如果Need[i][j]=k,那么进程Pj还需要资源Rj的k个实例。
注：Need[i][j] = Max[i][j] – Allocation [i][j]

为了描述方便，我们采用一些简化的表示方法：

　　设X和Y为长度为n的向量，则X <= Y当且仅当对所有i = 1，2，...，n，X[i] <= Y[i]。例如，如果X = (1,7,2,3)而Y = (0,3,2,1)，那么Y <= X。如果Y <= X且Y != X，那么Y < X。

　　可以将Allocation和Need的每行作为向量，并分别用Allocation i和Need i来表示，向量Allocation i表示分配给进程Pi的资源；向量Need i表示进程为完成其任务可能仍然需要申请的额外资源。

银行家算法可整体分成两个部分：

1.安全性算法

确认计算机系统是否处于安全状态的算法分为如下几步：

（1）设Work和Finish分别为长度为m和n的向量。按如下方式进行初始化，Work = Avaliable且对于i = 0,1，...，n - 1，Finish[i] = 　　 false。

（2）查找这样的i使其满足

　　·Finish[i] = false

　　·Need i <= Work

　　如果没有这样的i，那么就转到第（4）步。

（3）Work = Work + Allocation i

　　 Finish[i] = true

　　 返回第（2）步

（4）如果对所有i，Finish[i] = true，那么系统则处于安全状态。

该算法可能需要m * n^2数量级的操作以确定系统是否处于安全状态。

2.资源请求算法

现在，描述如何判断是否可安全允许请求的算法。

　　设Request i为进程Pi的请求向量。如果Request i[j] == k，那么进程Pi需要资源类型Rj的实例数量为k。当进程Pi作出资源请求时，采取如下动作：

（1）如果Request i <= Need i，那么转到第（2）步。否则，产生出错条件，这是因为进程Pi已超过了其最大请求。

（2）如果Request i <= Available，那么转到第（3）步。否则，Pi必须等待，这是因为没有可用资源。

（3）假定系统可以分配给进程Pi所请求的资源，并按如下方式修改状态：

　　 Available = Available - Request i;

　　 Allocation i = Allocation i + Request i;

　　 Need i = Need i - Request i;

　　如果所产生的资源分配状态是安全的（通过上面的安全性算法），那么Pi可分配到它所请求的资源。但是，如果新状态不安全，则进程Pi必须等待Request i并恢复到原来的资源分配状态。

上面都是一些表达式，可能有些枯燥，现在我们来练习一道例题：

　　考虑这样一个系统，有5个进程P0~P4，3种资源类型A、B、C。资源类型A有10个实例，资源类型B有5个实例，资源类型C有7个实例。假定在时刻T0，系统状态如下：

		Allocation		Max		Avaliable
		 A  B  C      A  B  C    A  B  C
P0		 0  1  0      7  5  3    3  3  2
P1       2  0  0      3  2  2
P2       3  0  2      9  0  2
P3       2  1  1      2  2  2
P4       0  0  2      4  3  3

　　矩阵Need的内容定义成Max-Allocation：

 	   	  Need
		 A  B  C
P0		 7  4  3
P1       1  2  2
P2       6  0  0
P3       0  1  1
P4       4  3  1

　　可认为系统现在处于安全状态，因为存在一个安全序列<P1,P3,P4,P2,P0>。

　　现在假定进程P1再请求1个A类资源和两个C类资源，这样Request1 = (1,0,2)。为了确定这个请求是否可以立即允许，首先检测Request1 <= Available(即，(1,0,2) <= (3,3,2))，其值为真。接着假定这个请求被满足，会产生如下新状态：

		Allocation	   Need		Avaliable
		 A  B  C      A  B  C    A  B  C
P0		 0  1  0      7  4  3    2  3  0
P1       3  0  2      0  2  0
P2       3  0  2      6  0  0
P3       2  1  1      0  1  1
P4       0  0  2      4  3  1

　　必须确定这个状态是否安全。为此，执行安全算法，并找到顺序<P1,P3,P4,P0,P2>满足安全要求。因此，可以立即允许进程P1的这个请求。

　　然而，可以发现当系统处于这一状态时，是不能允许P4的请求(3,3,0)的，因为没有那么多资源可用。也不能允许P0的请求(0,2,0)；虽然有资源可用，但是这会导致系统处于不安全状态。