【复习】密码算法——AES

0 AES简介

　　1997年1月2号，美国国家标准技术研究所宣布希望征集一个安全性能更高的加密算法（AES）[3]，用以取代DES。我们知道DES的密钥长度是64 bits，但实际加解密中使用的有效长度只有56 bits，因此算法的理论安全性是256。但随着制造工艺的不断进步，计算机的计算能力也越来越强，DES将不能提供足够的安全性。AES得到了全世界很多密码工作者的响应，先后有很多人提交了自己的设计方案。截止到最后一轮评选，仍然有5个候选算法：Rijndael，Serpent，Twofish，RC6和MARS。最终经过严格的性能测评，Rijndael算法获胜，因此AES算法也叫Rijndael。

　　AES由Joan Daemen和Vincent Rijmen设计。根据算法密钥的长度，AES有3种不同方案用以满足不同的场景需求，分别是AES-128、AES-192和AES-256。本文主要对AES-128进行介绍，另外两种的思路基本一样，只是密钥扩展的过程会稍有不同，加解密的轮数会适当增加，但加解密的操作都是一样的。

　　接下来让我们一起探讨AES内部的结构。

　　（本文只是对AES算法的各个部件、基本原理进行简单介绍，旨在加深对算法流程的了解。在正式软件运用中也不推荐自己编写代码，很多开源项目都有实现；如果是为了加深对算法实现细节的了解，写写也挺好的。AES算法的部件在对称密码领域特别是分组密码领域常有使用，但由于数学知识的缺陷，S盒以及列混淆中使用的矩阵的很多性质没有进行介绍，读者有兴趣可以自行参考相关文献。）

1 算法流程

　　AES加解密的流程图如下：

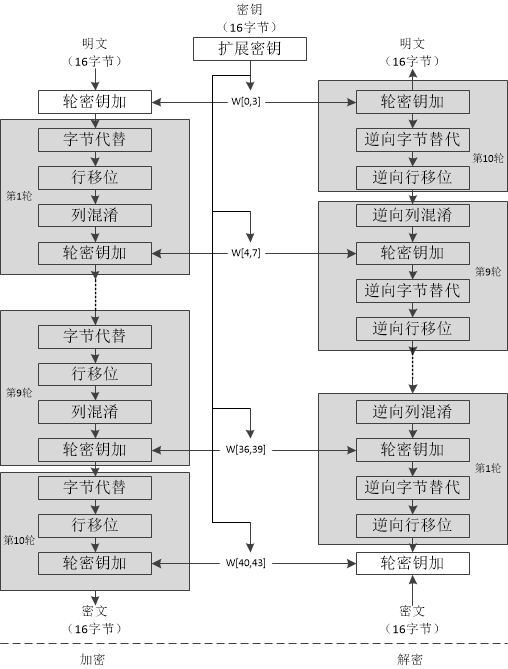
　　AES加密过程涉及到4种操作：字节替代（SubBytes）、行移位（ShiftRows）、列混淆（MixColumns）和轮密钥加（AddRoundKey）。从上图可以看出：1）解密过程的每一步分别对应操作的逆操作，2）加解密所有操作的顺序正好是相反的。正是由于这两点保证了解密能够正确地恢复明文。加解密中每轮的密钥分别由初始密钥扩展得到。算法中16字节的明文、密文和轮密钥都以一个4x4的矩阵表示。

　　接下来分别对上述5种操作进行介绍。

1.1 字节代替

　　字节代替的主要功能是通过S盒完成一个字节到另外一个字节的映射。S盒的详细构造方法可以参考文献[1]。这里直接给出构造好的结果，下图(a)为S盒，图(b)为S-1（S盒的逆）。

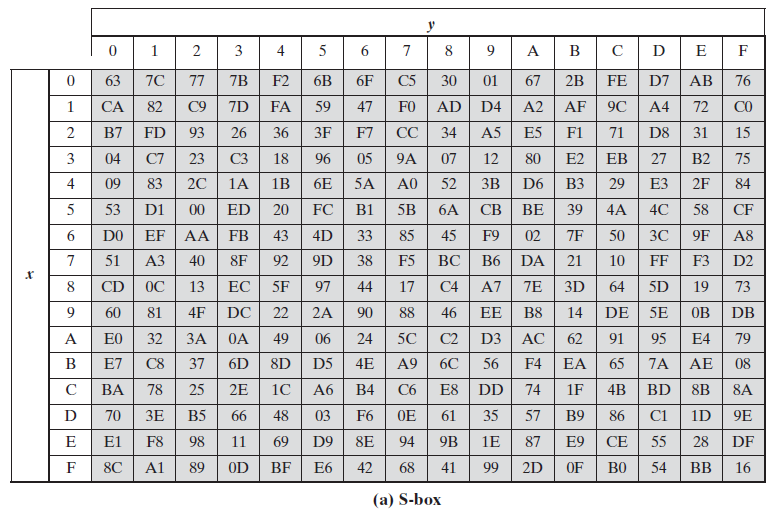
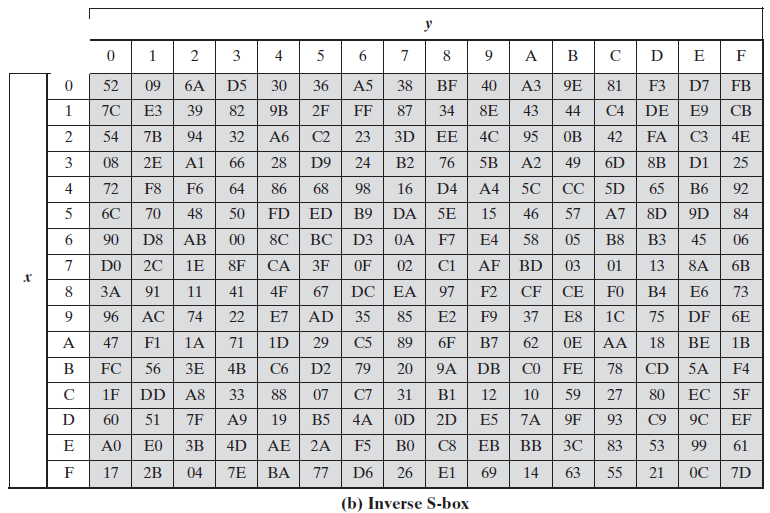
　　S和S-1分别为16x16的矩阵。输入的高4-bit对应的值作为行标，低4-bit对应的值作为列标；假设输入字节的值为a=a7a6a5a4a3a2a1a0，则输出值为S[a7a6a5a4][a3a2a1a0]，S-1的变换也同理。

　　例如：字节00000000B替换后的值为（S[0][0]=）63H，再通过S-1即可得到替换前的值，（S-1 [6][3]=）00H。

1.2 行移位

　　行移位的功能是实现一个4x4矩阵内部字节之间的置换。

1.2.1 正向行移位

　　正向行移位的原理图如下：

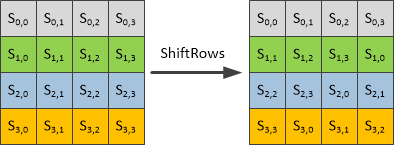
　　实际移位的操作即是：第一行保存不变，第二行循环左移1个字节，第三行循环左移2个字节，第四行循环左移3个字节。假设矩阵的名字为state，用公式表示如下：state’[i][j] = state[i][(j+i)%4];其中i、j属于[0,3]

1.2.2 逆向行移位

　　逆向行移位即是相反的操作，用公式表示如下：state’[i][j] = state[i][(4+j-i)%4];其中i、j属于[0,3]

　　到这里差不多完成一半了……

1.3 列混淆

　　列混淆：利用GF(28)域上算术特性的一个代替。

1.3.1 正向列混淆

　　正向列混淆的原理图如下：

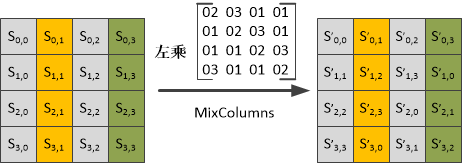
　　根据矩阵的乘法可知，在列混淆的过程中，每个字节对应的值只与该列的4个值有关系。此处的乘法和加法都是定义在GF(28)上的，需要注意如下几点：

　　　　1) 将某个字节所对应的值乘以2，其结果就是将该值的二进制位左移一位，如果原始值的最高位为1，则还需要将移位后的结果异或00011011；[1]

　　　　　　英文原文描述如下：In particular, multiplication of a value by x (i.e., by {02}) can be implemented as a 1-bit left shift followed by a conditional bitwise XOR with (0001 1011) if the leftmost bit of the original value (prior to the shift) is 1.

　　　　2) 乘法对加法满足分配率，例如：07·S0,0=(01⊕02⊕04)·S0,0= S0,0⊕(02·S0,0)(04·S0,0)

　　　　3) 此处的矩阵乘法与一般意义上矩阵的乘法有所不同，各个值在相加时使用的是模2加法（异或运算）。

　　

　　下面举一个例子，假设某一列的值如下图，运算过程如下：

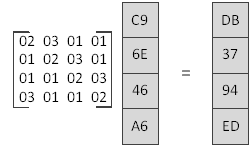
　　在计算02与C9的乘积时，由于C9对应最左边的比特为1，因此需要将C9左移一位后的值与(0001 1011)求异或。同理可以求出另外几个值。

1.3.2 逆向列混淆

　　逆向列混淆的原理图如下：

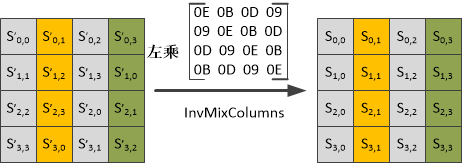
　　由于：

　　说明两个矩阵互逆，经过一次逆向列混淆后即可恢复原文。

1.4 轮密码加

　　这个操作相对简单，其依据的原理是“任何数和自身的异或结果为0”。加密过程中，每轮的输入与轮密钥异或一次；因此，解密时再异或上该轮的密钥即可恢复输入。

1.5 密钥扩展

　　密钥扩展的原理图如下：

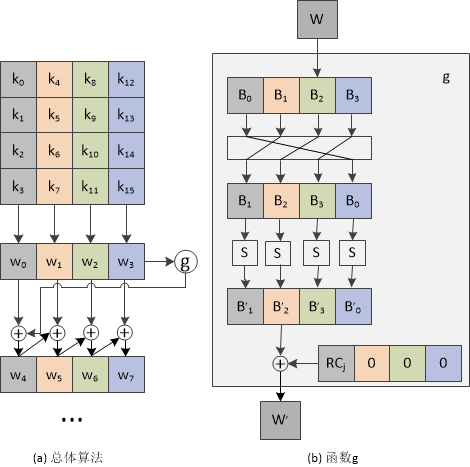
　　密钥扩展过程说明：

　　　　1)  将初始密钥以列为主，转化为4个32 bits的字，分别记为w[0…3]；

　　　　2)  按照如下方式，依次求解w[j]，其中j是整数并且属于[4,43]；

　　　　3)  若j%4=0,则w[j]=w[j-4]⊕g(w[j-1]),否则w[j]=w[j-4]⊕w[j-1]；

　　函数g的流程说明：

　　　　4)  将w循环左移一个字节；

　　　　5)  分别对每个字节按S盒进行映射；

　　　　6)  与32 bits的常量（RC[j/4],0,0,0）进行异或，RC是一个一维数组，其值如下。（RC的值只需要有10个，而此处用了11个，实际上RC[0]在运算中没有用到，增加RC[0]是为了便于程序中用数组表示。由于j的最小取值是4，j/4的最小取值则是1，因此不会产生错误。）

　　　　　　RC = {00, 01, 02, 04, 08, 10, 20, 40, 80, 1B, 36}

　　好吧，整个加密过程就是这样，终于介绍完了……

　　解密过程直接进行逆操作即可，但是为了减少硬件面积，可以通过对解密的操作进行适当调换，再使用与加密相同的硬件电路。

1.6 小结

　　密码算法要求是可逆的，这样解密才能正确的恢复明文。拿AES来说，在密钥固定的情况下，明文和密文在整个输入空间是一一对应的。因此算法的各个部件也都是可逆的，再将各个部件的操作顺序设计成可逆的，密文就能正确的解密了。