【BZOJ1043】下落的圆盘 [计算几何]

下落的圆盘

Time Limit: 10 Sec  Memory Limit: 162 MB
[Submit][Status][Discuss]

Description

　　有n个圆盘从天而降，后面落下的可以盖住前面的。求最后形成的封闭区域的周长。

　　看下面这副图, 所有的红色线条的总长度即为所求。

　　

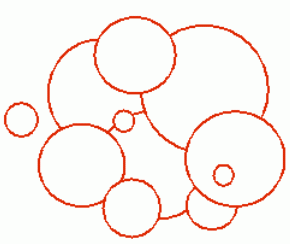
Input

　　第一行为1个整数n
　　接下来n行每行3个实数,ri,xi,yi,表示下落时第i个圆盘的半径和圆心坐标.

Output

　　最后的周长，保留三位小数

Sample Input

　　2
　　1 0 0
　　1 1 0

Sample Output

　　10.472

HINT

　　n <= 1000

Solution

　　显然是一道计算几何题。

　　考虑一个圆对于答案的贡献，显然是这个圆的周长 - 后面的圆把它覆盖掉的周长的并。那么我们就考虑怎么求这个并。

　　先考虑怎样记录下一个答案，显然直接扣掉单个圆对它的覆盖是不可行的，要减去重叠的情况。

　　既然边不可行，我们就用角度。显然，若我们求出 两圆交点的角度 即可解决这题。

　　我们考虑求圆A被圆B覆盖的角度：现在我们有两个圆的半径、圆心距。我们就可以得到 圆A与圆B的圆心连线 与 圆A半径 的夹角。

　　我们也可以知道 圆A与圆B的圆心连线 与 x轴的夹角。

　　这样的话，就可以把单个圆对于它的贡献记录到栈里面，最后扫一遍求一下剩余的角度，乘上R就是它对于答案的贡献了。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<queue>
 using namespace std;
 typedef unsigned long long s64;

 const int ONE = ;
 const double pi = acos(-1.0);

 int n;
 struct power
 {
         double x, y, r;
 }a[ONE];

 struct circle
 {
         double a, b;
 }stk[ONE];
 int top;

 double Ans;

 bool cmp(const circle &a, const circle &b)
 {
         if(a.a != b.a) return a.a < b.a;
         return a.b < b.b;
 }

 int get()
 {
         int res,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 double sqr(double x) {return x * x;}
 double dist(power a, power b) {return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));}

 double Calc(power a, power b)
 {
         double A = a.r, B = b.r, C = dist(a, b);
         double cosB = (sqr(A) + sqr(C) - sqr(B)) / ( * A * C);
         double angle = atan2(a.x - b.x, a.y - b.y), add = acos(cosB);
         stk[++top] = (circle){angle - add, angle + add};
 }

 double init(power a, power b) {return a.r + dist(a, b) <= b.r;}
 double sect(power a, power b) {return fabs(a.r - b.r) < dist(a, b) && dist(a, b) < a.r + b.r;}

 double Deal(int id)
 {
         top = ;
         for(int i = id+; i <= n; i++)
             if(init(a[id], a[i])) return ;

         for(int i = id+; i <= n; i++)
             if(sect(a[id], a[i])) Calc(a[id], a[i]);

         for(int i = ; i <= top; i++)
         {
             while(stk[i].a < ) stk[i].a +=  * pi;
             while(stk[i].b < ) stk[i].b +=  * pi;
             if(stk[i].a > stk[i].b) stk[++top] = (circle){, stk[i].b}, stk[i].b = *pi;
         }

         sort(stk + , stk + top + , cmp);
         double last = 0.0, sum = 0.0;
         for(int i = ; i <= top; i++)
             if(stk[i].a > last) sum += stk[i].a - last, last = stk[i].b;
             else last = max(last, stk[i].b);

         sum +=  * pi - last;
         return a[id].r * sum;
 }

 int main()
 {
         n = get();
         for(int i = ; i <= n; i++)
             scanf("%lf %lf %lf", &a[i].r, &a[i].x, &a[i].y);
         for(int i = ; i <= n; i++)
             Ans += Deal(i);
         printf("%.3lf", Ans);
 }