伸展树(三)之 Java的实现
概要
前面分别通过C和C++实现了伸展树，本章给出伸展树的Java版本。基本算法和原理都与前两章一样。
1. 伸展树的介绍
2. 伸展树的Java实现(完整源码)
3. 伸展树的Java测试程序
转载请注明出处：http://www.cnblogs.com/skywang12345/p/3604286.html
更多内容: 数据结构与算法系列 目录
(01) 伸展树(一)之 图文解析 和 C语言的实现
(02) 伸展树(二)之 C++的实现
(03) 伸展树(三)之 Java的实现
伸展树的介绍
伸展树(Splay Tree)是特殊的二叉查找树。
它的特殊是指，它除了本身是棵二叉查找树之外，它还具备一个特点: 当某个节点被访问时，伸展树会通过旋转使该节点成为树根。这样做的好处是，下次要访问该节点时，能够迅速的访问到该节点。
伸展树的Java实现
1. 基本定义
public class SplayTree<T extends Comparable<T>> {
private SplayTreeNode<T> mRoot; // 根结点
public class SplayTreeNode<T extends Comparable<T>> {
T key; // 关键字(键值)
SplayTreeNode<T> left; // 左孩子
SplayTreeNode<T> right; // 右孩子
public SplayTreeNode() {
this.left = null;
this.right = null;
}
public SplayTreeNode(T key, SplayTreeNode<T> left, SplayTreeNode<T> right) {
this.key = key;
this.left = left;
this.right = right;
}
}
...
}
SplayTree是伸展树，而SplayTreeNode是伸展树节点。在此，我将SplayTreeNode定义为SplayTree的内部类。在伸展树SplayTree中包含了伸展树的根节点mRoot。SplayTreeNode包括的几个组成元素:
(01) key -- 是关键字，是用来对伸展树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。
2. 旋转
旋转是伸展树中需要重点关注的，它的代码如下：
/*
* 旋转key对应的节点为根节点，并返回根节点。
*
* 注意：
* (a)：伸展树中存在"键值为key的节点"。
* 将"键值为key的节点"旋转为根节点。
* (b)：伸展树中不存在"键值为key的节点"，并且key < tree.key。
* b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
* b-2 "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
* (c)：伸展树中不存在"键值为key的节点"，并且key > tree.key。
* c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
* c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
*/
private SplayTreeNode<T> splay(SplayTreeNode<T> tree, T key) {
if (tree == null)
return tree; SplayTreeNode<T> N = new SplayTreeNode<T>();
SplayTreeNode<T> l = N;
SplayTreeNode<T> r = N;
SplayTreeNode<T> c; for (;;) { int cmp = key.compareTo(tree.key);
if (cmp < 0) { if (tree.left == null)
break; if (key.compareTo(tree.left.key) < 0) {
c = tree.left; /* rotate right */
tree.left = c.right;
c.right = tree;
tree = c;
if (tree.left == null)
break;
}
r.left = tree; /* link right */
r = tree;
tree = tree.left;
} else if (cmp > 0) { if (tree.right == null)
break; if (key.compareTo(tree.right.key) > 0) {
c = tree.right; /* rotate left */
tree.right = c.left;
c.left = tree;
tree = c;
if (tree.right == null)
break;
} l.right = tree; /* link left */
l = tree;
tree = tree.right;
} else {
break;
}
} l.right = tree.left; /* assemble */
r.left = tree.right;
tree.left = N.right;
tree.right = N.left; return tree;
} public void splay(T key) {
mRoot = splay(mRoot, key);
}
上面的代码的作用：将"键值为key的节点"旋转为根节点，并返回根节点。它的处理情况共包括：
(a)：伸展树中存在"键值为key的节点"。
将"键值为key的节点"旋转为根节点。
(b)：伸展树中不存在"键值为key的节点"，并且key < tree->key。
b-1) "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
b-2) "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
(c)：伸展树中不存在"键值为key的节点"，并且key > tree->key。
c-1) "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
c-2) "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
下面列举个例子分别对a进行说明。
在下面的伸展树中查找10，，共包括"右旋" --> "右链接" --> "组合"这3步。
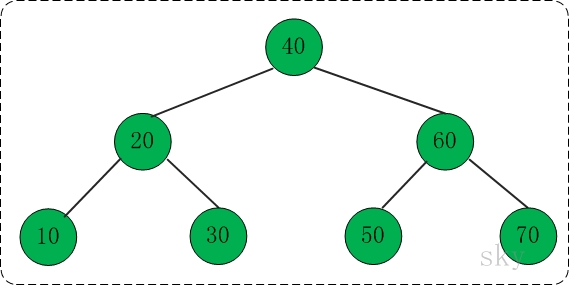
01, 右旋
对应代码中的"rotate right"部分
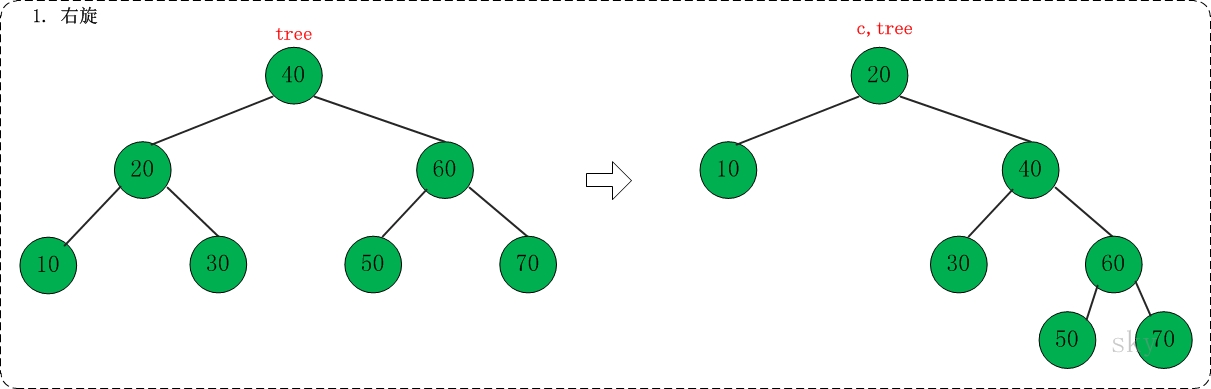
02, 右链接
对应代码中的"link right"部分
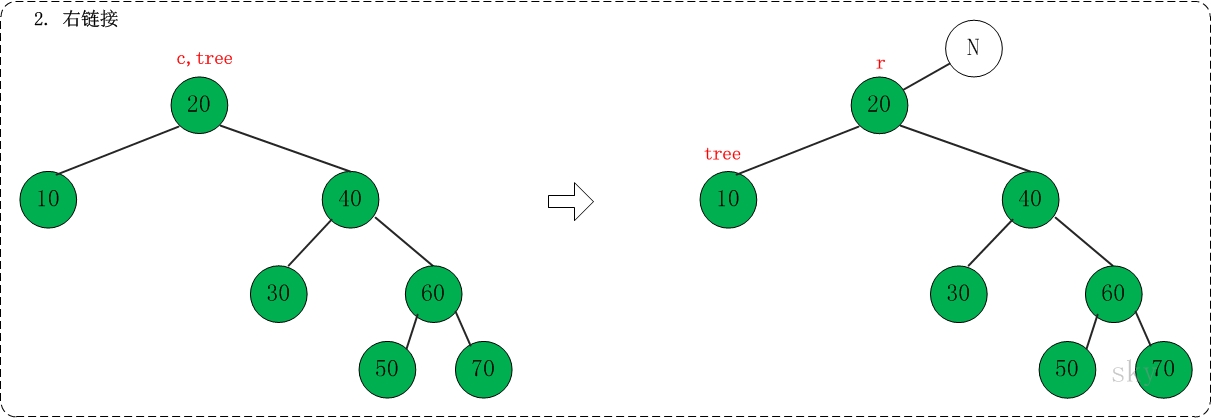
03. 组合
对应代码中的"assemble"部分
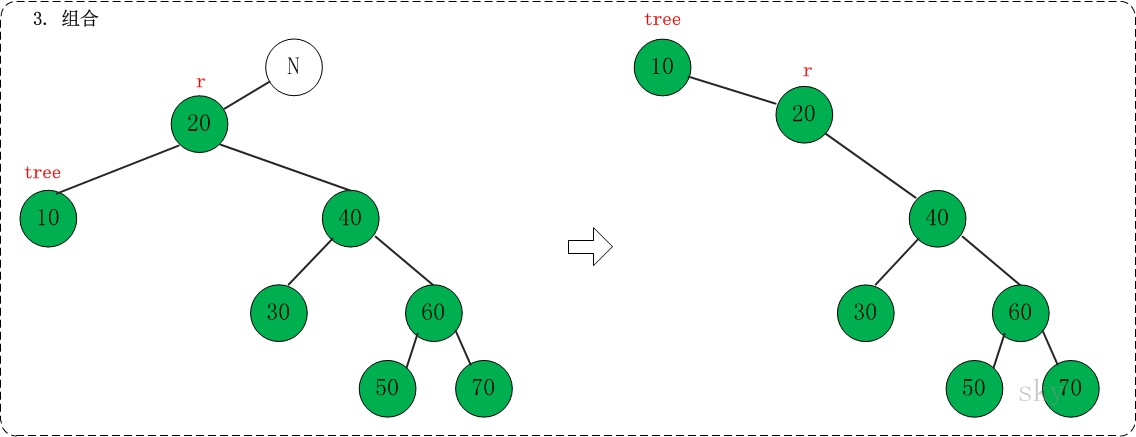
提示：如果在上面的伸展树中查找"70"，则正好与"示例1"对称，而对应的操作则分别是"rotate left", "link left"和"assemble"。
其它的情况，例如"查找15是b-1的情况，查找5是b-2的情况"等等，这些都比较简单，大家可以自己分析。
3. 插入
插入代码
/*
* 将结点插入到伸展树中，并返回根节点
*
* 参数说明：
* tree 伸展树的
* z 插入的结点
*/
private SplayTreeNode<T> insert(SplayTreeNode<T> tree, SplayTreeNode<T> z) {
int cmp;
SplayTreeNode<T> y = null;
SplayTreeNode<T> x = tree; // 查找z的插入位置
while (x != null) {
y = x;
cmp = z.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else {
System.out.printf("不允许插入相同节点(%d)!\n", z.key);
z=null;
return tree;
}
} if (y==null)
tree = z;
else {
cmp = z.key.compareTo(y.key);
if (cmp < 0)
y.left = z;
else
y.right = z;
} return tree;
} public void insert(T key) {
SplayTreeNode<T> z=new SplayTreeNode<T>(key,null,null); // 如果新建结点失败，则返回。
if ((z=new SplayTreeNode<T>(key,null,null)) == null)
return ; // 插入节点
mRoot = insert(mRoot, z);
// 将节点(key)旋转为根节点
mRoot = splay(mRoot, key);
}
insert(key)是提供给外部的接口，它的作用是新建节点(节点的键值为key)，并将节点插入到伸展树中；然后，将该节点旋转为根节点。
insert(tree, z)是内部接口，它的作用是将节点z插入到tree中。insert(tree, z)在将z插入到tree中时，仅仅只将tree当作是一棵二叉查找树，而且不允许插入相同节点。
4. 删除
删除代码
/*
* 删除结点(z)，并返回被删除的结点
*
* 参数说明：
* bst 伸展树
* z 删除的结点
*/
private SplayTreeNode<T> remove(SplayTreeNode<T> tree, T key) {
SplayTreeNode<T> x; if (tree == null)
return null; // 查找键值为key的节点，找不到的话直接返回。
if (search(tree, key) == null)
return tree; // 将key对应的节点旋转为根节点。
tree = splay(tree, key); if (tree.left != null) {
// 将"tree的前驱节点"旋转为根节点
x = splay(tree.left, key);
// 移除tree节点
x.right = tree.right;
}
else
x = tree.right; tree = null; return x;
} public void remove(T key) {
mRoot = remove(mRoot, key);
}
remove(key)是外部接口，remove(tree, key)是内部接口。
remove(tree, key)的作用是：删除伸展树中键值为key的节点。
它会先在伸展树中查找键值为key的节点。若没有找到的话，则直接返回。若找到的话，则将该节点旋转为根节点，然后再删除该节点。
关于"前序遍历"、"中序遍历"、"后序遍历"、"最大值"、"最小值"、"查找"、"打印伸展树"、"销毁伸展树"等接口就不再单独介绍了，Please RTFSC(Read The Fucking Source Code)！这些接口，与前面介绍的"二叉查找树"、"AVL树"的相关接口都是类似的。
伸展树的Java实现(完整源码)
伸展树的实现文件(SplayTree.java)
/**
* Java 语言: 伸展树
*
* @author skywang
* @date 2014/02/03
*/ public class SplayTree<T extends Comparable<T>> { private SplayTreeNode<T> mRoot; // 根结点 public class SplayTreeNode<T extends Comparable<T>> {
T key; // 关键字(键值)
SplayTreeNode<T> left; // 左孩子
SplayTreeNode<T> right; // 右孩子 public SplayTreeNode() {
this.left = null;
this.right = null;
} public SplayTreeNode(T key, SplayTreeNode<T> left, SplayTreeNode<T> right) {
this.key = key;
this.left = left;
this.right = right;
}
} public SplayTree() {
mRoot=null;
} /*
* 前序遍历"伸展树"
*/
private void preOrder(SplayTreeNode<T> tree) {
if(tree != null) {
System.out.print(tree.key+" ");
preOrder(tree.left);
preOrder(tree.right);
}
} public void preOrder() {
preOrder(mRoot);
} /*
* 中序遍历"伸展树"
*/
private void inOrder(SplayTreeNode<T> tree) {
if(tree != null) {
inOrder(tree.left);
System.out.print(tree.key+" ");
inOrder(tree.right);
}
} public void inOrder() {
inOrder(mRoot);
} /*
* 后序遍历"伸展树"
*/
private void postOrder(SplayTreeNode<T> tree) {
if(tree != null)
{
postOrder(tree.left);
postOrder(tree.right);
System.out.print(tree.key+" ");
}
} public void postOrder() {
postOrder(mRoot);
} /*
* (递归实现)查找"伸展树x"中键值为key的节点
*/
private SplayTreeNode<T> search(SplayTreeNode<T> x, T key) {
if (x==null)
return x; int cmp = key.compareTo(x.key);
if (cmp < 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
} public SplayTreeNode<T> search(T key) {
return search(mRoot, key);
} /*
* (非递归实现)查找"伸展树x"中键值为key的节点
*/
private SplayTreeNode<T> iterativeSearch(SplayTreeNode<T> x, T key) {
while (x!=null) {
int cmp = key.compareTo(x.key); if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else
return x;
} return x;
} public SplayTreeNode<T> iterativeSearch(T key) {
return iterativeSearch(mRoot, key);
} /*
* 查找最小结点：返回tree为根结点的伸展树的最小结点。
*/
private SplayTreeNode<T> minimum(SplayTreeNode<T> tree) {
if (tree == null)
return null; while(tree.left != null)
tree = tree.left;
return tree;
} public T minimum() {
SplayTreeNode<T> p = minimum(mRoot);
if (p != null)
return p.key; return null;
} /*
* 查找最大结点：返回tree为根结点的伸展树的最大结点。
*/
private SplayTreeNode<T> maximum(SplayTreeNode<T> tree) {
if (tree == null)
return null; while(tree.right != null)
tree = tree.right;
return tree;
} public T maximum() {
SplayTreeNode<T> p = maximum(mRoot);
if (p != null)
return p.key; return null;
} /*
* 旋转key对应的节点为根节点，并返回根节点。
*
* 注意：
* (a)：伸展树中存在"键值为key的节点"。
* 将"键值为key的节点"旋转为根节点。
* (b)：伸展树中不存在"键值为key的节点"，并且key < tree.key。
* b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
* b-2 "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
* (c)：伸展树中不存在"键值为key的节点"，并且key > tree.key。
* c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
* c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
*/
private SplayTreeNode<T> splay(SplayTreeNode<T> tree, T key) {
if (tree == null)
return tree; SplayTreeNode<T> N = new SplayTreeNode<T>();
SplayTreeNode<T> l = N;
SplayTreeNode<T> r = N;
SplayTreeNode<T> c; for (;;) { int cmp = key.compareTo(tree.key);
if (cmp < 0) { if (tree.left == null)
break; if (key.compareTo(tree.left.key) < 0) {
c = tree.left; /* rotate right */
tree.left = c.right;
c.right = tree;
tree = c;
if (tree.left == null)
break;
}
r.left = tree; /* link right */
r = tree;
tree = tree.left;
} else if (cmp > 0) { if (tree.right == null)
break; if (key.compareTo(tree.right.key) > 0) {
c = tree.right; /* rotate left */
tree.right = c.left;
c.left = tree;
tree = c;
if (tree.right == null)
break;
} l.right = tree; /* link left */
l = tree;
tree = tree.right;
} else {
break;
}
} l.right = tree.left; /* assemble */
r.left = tree.right;
tree.left = N.right;
tree.right = N.left; return tree;
} public void splay(T key) {
mRoot = splay(mRoot, key);
} /*
* 将结点插入到伸展树中，并返回根节点
*
* 参数说明：
* tree 伸展树的
* z 插入的结点
*/
private SplayTreeNode<T> insert(SplayTreeNode<T> tree, SplayTreeNode<T> z) {
int cmp;
SplayTreeNode<T> y = null;
SplayTreeNode<T> x = tree; // 查找z的插入位置
while (x != null) {
y = x;
cmp = z.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else {
System.out.printf("不允许插入相同节点(%d)!\n", z.key);
z=null;
return tree;
}
} if (y==null)
tree = z;
else {
cmp = z.key.compareTo(y.key);
if (cmp < 0)
y.left = z;
else
y.right = z;
} return tree;
} public void insert(T key) {
SplayTreeNode<T> z=new SplayTreeNode<T>(key,null,null); // 如果新建结点失败，则返回。
if ((z=new SplayTreeNode<T>(key,null,null)) == null)
return ; // 插入节点
mRoot = insert(mRoot, z);
// 将节点(key)旋转为根节点
mRoot = splay(mRoot, key);
} /*
* 删除结点(z)，并返回被删除的结点
*
* 参数说明：
* bst 伸展树
* z 删除的结点
*/
private SplayTreeNode<T> remove(SplayTreeNode<T> tree, T key) {
SplayTreeNode<T> x; if (tree == null)
return null; // 查找键值为key的节点，找不到的话直接返回。
if (search(tree, key) == null)
return tree; // 将key对应的节点旋转为根节点。
tree = splay(tree, key); if (tree.left != null) {
// 将"tree的前驱节点"旋转为根节点
x = splay(tree.left, key);
// 移除tree节点
x.right = tree.right;
}
else
x = tree.right; tree = null; return x;
} public void remove(T key) {
mRoot = remove(mRoot, key);
} /*
* 销毁伸展树
*/
private void destroy(SplayTreeNode<T> tree) {
if (tree==null)
return ; if (tree.left != null)
destroy(tree.left);
if (tree.right != null)
destroy(tree.right); tree=null;
} public void clear() {
destroy(mRoot);
mRoot = null;
} /*
* 打印"伸展树"
*
* key -- 节点的键值
* direction -- 0，表示该节点是根节点;
* -1，表示该节点是它的父结点的左孩子;
* 1，表示该节点是它的父结点的右孩子。
*/
private void print(SplayTreeNode<T> tree, T key, int direction) { if(tree != null) { if(direction==0) // tree是根节点
System.out.printf("%2d is root\n", tree.key);
else // tree是分支节点
System.out.printf("%2d is %2d's %6s child\n", tree.key, key, direction==1?"right" : "left"); print(tree.left, tree.key, -1);
print(tree.right,tree.key, 1);
}
} public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
}
伸展树的测试程序(SplayTreeTest.java)
/**
* Java 语言: 伸展树
*
* @author skywang
* @date 2014/02/03
*/
public class SplayTreeTest { private static final int arr[] = {10,50,40,30,20,60}; public static void main(String[] args) {
int i, ilen;
SplayTree<Integer> tree=new SplayTree<Integer>(); System.out.print("== 依次添加: ");
ilen = arr.length;
for(i=0; i<ilen; i++) {
System.out.print(arr[i]+" ");
tree.insert(arr[i]);
} System.out.print("\n== 前序遍历: ");
tree.preOrder(); System.out.print("\n== 中序遍历: ");
tree.inOrder(); System.out.print("\n== 后序遍历: ");
tree.postOrder();
System.out.println(); System.out.println("== 最小值: "+ tree.minimum());
System.out.println("== 最大值: "+ tree.maximum());
System.out.println("== 树的详细信息: ");
tree.print(); i = 30;
System.out.printf("\n== 旋转节点(%d)为根节点\n", i);
tree.splay(i);
System.out.printf("== 树的详细信息: \n");
tree.print(); // 销毁二叉树
tree.clear();
}
}
在二叉查找树的Java实现中，使用了泛型，也就意味着它支持任意类型；但是该类型必须要实现Comparable接口。
伸展树的Java测试程序
伸展树的测试程序运行结果如下：
== 依次添加: 10 50 40 30 20 60
== 前序遍历: 60 30 20 10 50 40
== 中序遍历: 10 20 30 40 50 60
== 后序遍历: 10 20 40 50 30 60
== 最小值: 10
== 最大值: 60
== 树的详细信息:
60 is root
30 is 60's left child
20 is 30's left child
10 is 20's left child
50 is 30's right child
40 is 50's left child == 旋转节点(30)为根节点
== 树的详细信息:
30 is root
20 is 30's left child
10 is 20's left child
60 is 30's right child
50 is 60's left child
40 is 50's left child
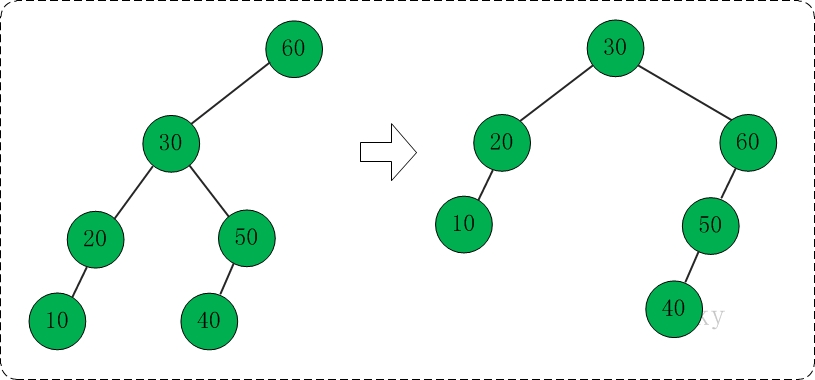
测试程序的主要流程是：新建伸展树，然后向伸展树中依次插入10,50,40,30,20,60。插入完毕这些数据之后，伸展树的节点是60；此时，再旋转节点，使得30成为根节点。
依次插入10,50,40,30,20,60示意图如下：
将30旋转为根节点的示意图如下：
伸展树(三)之 Java的实现的更多相关文章
- AVL树(三)之 Java的实现
概要 前面分别介绍了AVL树"C语言版本"和"C++版本",本章介绍AVL树的Java实现版本,它的算法与C语言和C++版本一样.内容包括:1. AVL树的介绍 ...
- 哈夫曼树(三)之 Java详解
前面分别通过C和C++实现了哈夫曼树,本章给出哈夫曼树的java版本. 目录 1. 哈夫曼树的介绍 2. 哈夫曼树的图文解析 3. 哈夫曼树的基本操作 4. 哈夫曼树的完整源码 转载请注明出处:htt ...
- 伸展树(一)之 图文解析 和 C语言的实现
概要 本章介绍伸展树.它和"二叉查找树"和"AVL树"一样,都是特殊的二叉树.在了解了"二叉查找树"和"AVL树"之后, ...
- 伸展树(二)之 C++的实现
概要 上一章介绍了伸展树的基本概念,并通过C语言实现了伸展树.本章是伸展树的C++实现,后续再给出Java版本.还是那句老话,它们的原理都一样,择其一了解即可. 目录1. 伸展树的介绍2. 伸展树的C ...
- 伸展树--java
文字转载自:http://www.cnblogs.com/vamei 代码转载自:http://www.blogjava.net/javacap/archive/2007/12/19/168627.h ...
- 【BBST 之伸展树 (Splay Tree)】
最近“hiho一下”出了平衡树专题,这周的Splay一直出现RE,应该删除操作指针没处理好,还没找出原因. 不过其他操作运行正常,尝试用它写了一道之前用set做的平衡树的题http://codefor ...
- 数据结构（二） --- 伸展树（Splay Tree）
文章图片和代码来自邓俊辉老师课件 概述 伸展树(Splay Tree),也叫分裂树,是一种二叉排序树,它能在O(log n)内完成插入.查找和删除操作.它由丹尼尔·斯立特Daniel Sleator ...
- 树状结构Java模型、层级关系Java模型、上下级关系Java模型与html页面展示
树状结构Java模型.层级关系Java模型.上下级关系Java模型与html页面展示 一.业务原型:公司的组织结构.传销关系网 二.数据库模型 很简单,创建 id 与 pid 关系即可.(pid:pa ...
- Splay伸展树学习笔记
Splay伸展树 有篇Splay入门必看文章 —— CSDN链接 经典引文 空间效率:O(n) 时间效率:O(log n)插入.查找.删除 创造者:Daniel Sleator 和 Robert Ta ...
随机推荐
- curl上传、下载、https登陆
1.下载 $ch = curl_init(); curl_setopt($ch, CURLOPT_URL, "ftp://127.0.0.1/downtest.txt"); cur ...
- C#下取得Exif中照片拍摄日期
/// <summary> /// 获取Exif中的照片拍摄日期 /// </summary> /// <param name="fileName"& ...
- 内存缓存LruCache实现原理
自己项目中一直都是用的开源的xUtils框架,包括BitmapUtils.DbUtils.ViewUtils和HttpUtils四大模块,这四大模块都是项目中比较常用的.最近决定研究一下xUtils的 ...
- linux下redis设置密码登录
redis设置密码访问 你的redis在真是环境中不可以谁想访问就可以访问,所以必须要设置密码 设置密码的流程如下: vim /etc/redis.conf #requirepass foobare ...
- Unity3D去掉全屏时的屏幕黑边
给全屏后不在乎拉伸变形仍想让画面占满屏幕的朋友,网上搜了一上午,实在是没有相关的资料,只能自己琢磨了. 使用Canvas Scaler在全屏后Unity虽然会为我们自动拉伸UI,但拉伸后仍然保持我们在 ...
- 老罗学习MVC之旅：MVC组件分析
2System.Web.Mvc V 4.0.0.0 组件分析 2.1 Routing组件(路由选择) Routing的作用就是负责分析Url Action的要求• 必须是一个公有方法• 必须返回A ...
- 在Windows 2008/2008 R2 上配置IIS 7.0/7.5 故障转移集群
本文主要是从:http://support.microsoft.com/kb/970759/zh-cn,直接转载,稍作修改裁剪而来,其中红色粗体部分,是我特别要说明的 若要配置 IIS 7.0 和 7 ...
- Win7 32bit + Matlab2013b +Visual Studio 2010联合编程配置
要建立独立运行的C应用程序,系统中需要安装Matlab.Matlab编译器.C/C++编译器以及Matlab C/C++数学库函数和图形库函数. Matlab编译器使用mbuild命令可以直接将C/C ...
- System.Diagnostics.Stopwatch
System.Diagnostics.Stopwatch 注意:此类在 .NET Framework 2.0 版中是新增的.MSDN Stopwatch 实例可以测量一个时间间隔的运行时间,也可以测量 ...
- 新一代服务器性能测试工具Gatling
新一代服务器性能测试工具Gatlinghttp://automationqa.com/forum.php?mod=viewthread&tid=2898&fromuid=2