Potyczki Algorythmiczne 2019

Runda próbna：

A + B

设$f[i]$表示两数相加得到前$i$位的方案数，由$f[i-1]$和$f[i-2]$转移得到。

#include<cstdio>
#include<cstring>
typedef long long ll;
const int N=50;
int n,i,j,k,a[N],b[N][N];ll f[N];char s[N];
int main(){
  for(i=0;i<10;i++)for(j=0;j<10;j++){
    k=i+j;
    if(k<10)a[k]++;
    else b[k/10][k%10]++;
  }
  scanf("%s",s+1);
  n=strlen(s+1);
  for(i=1;i<=n;i++)s[i]-='0';
  f[0]=1;
  for(i=0;i<=n;i++){
    f[i+1]+=f[i]*a[s[i+1]];
    f[i+2]+=f[i]*b[s[i+1]][s[i+2]];
  }
  printf("%lld",f[n]);
}

　　

Runda 1：

Wina [B]

求出为了拿走每个数至少需要拿走几个数即可。

#include<cstdio>
const int N=2010;
int n,k,i,j,a[N][N],f[N][N],ans=~0U>>1;
int main(){
  scanf("%d%d",&n,&k);
  for(i=1;i<=n;i++)for(j=1;j<=i;j++)scanf("%d",&a[i][j]),f[i][j]=1;
  for(i=1;i<=n;i++)for(j=1;j<=i;j++){
    f[i][j]+=f[i-1][j-1]+f[i-1][j];
    if(i>=2)f[i][j]-=f[i-2][j-1];
    if(f[i][j]<=k&&a[i][j]<ans)ans=a[i][j];
  }
  printf("%d",ans);
}

　　

Muzyka pop [A]

数位DP，设$f[i][j][l][r]$表示已经考虑了二进制下最高$i$位，是否卡住上界为$j$，要在里面找数字分配给$a[l..r]$的最大得分，枚举分界线转移。

时间复杂度$O(n^3\log m)$。

#include<cstdio>
typedef long long ll;
const int N=67,M=205;
const ll inf=3000000000000000000LL;
int n,len,i,b[N];ll m,a[M],s[M],f[N][2][M][M];bool v[N][2][M][M];
inline void up(ll&a,ll b){a<b?(a=b):0;}
ll dfs(int x,int y,int l,int r){
  if(l>r)return 0;
  if(!x)return l==r?0:-inf;
  if(v[x][y][l][r])return f[x][y][l][r];
  v[x][y][l][r]=1;
  ll tmp=-inf;
  int ny=y;
  if(y==1&&b[x]==1)ny=0;
  up(tmp,dfs(x-1,ny,l,r));
  if(y==0||b[x]==1)for(int i=l;i<=r;i++)up(tmp,dfs(x-1,ny,l,i-1)+dfs(x-1,y,i,r)+s[r]-s[i-1]);
  return f[x][y][l][r]=tmp;
}
int main(){
  scanf("%d%lld",&n,&m);
  if(!m)return puts("0"),0;
  while(m)b[++len]=m&1,m>>=1;
  for(i=1;i<=n;i++)scanf("%lld",&a[i]),s[i]=s[i-1]+a[i];
  printf("%lld",dfs(len,1,1,n));
}

　　

Runda 2：

Herbata [B]

对于每种温度$i$，统计初始状态和最终状态下有多少升温度为$i$的水。按照温度从高到低模拟，如果任意时刻能量差非负且最后能量守恒，则合法。

时间复杂度$O(n\log n)$。

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=100010;
int Case,n,i,j,tmp,l,a,b;ll e;
struct E{int x,y;E(){}E(int _x,int _y){x=_x,y=_y;}}f[N],g[N];
inline bool cmp(const E&a,const E&b){return a.x<b.x;}
inline bool solve(){
  scanf("%d",&n);
  for(i=1;i<=n;i++){
    scanf("%d%d%d",&l,&a,&b);
    f[i]=E(a,l);
    g[i]=E(b,l);
  }
  sort(f+1,f+n+1,cmp);
  sort(g+1,g+n+1,cmp);
  for(i=j=1,e=0;i<=n;i++)while(f[i].y){
    while(!g[j].y)j++;
    tmp=min(f[i].y,g[j].y);
    f[i].y-=tmp;
    g[j].y-=tmp;
    e+=1LL*tmp*(g[j].x-f[i].x);
    if(e<0)return 0;
  }
  return !e;
}
int main(){
  scanf("%d",&Case);
  while(Case--)puts(solve()?"TAK":"NIE");
}

　　

Desant [A]

动态规划，设$f[i][S]$表示考虑了前$i$个数，这些数的选择情况为$S$的最小逆序对数以及对应的方案数。

状态优化：假设$[i+1,n]$这些数从小到大排序后是___X___X____X_____X___的形式，那么X__1__1__1_1X和X1111_______X是没有区别的。利用位运算和基数排序等方法可以将转移做到$O(1)$。

对于一个$i$来说，其状态数在最坏情况下等价于将$n$划分为若干个数的和，使得这些数的乘积最大，因此总状态数不超过$O(n3^{\frac{n}{3}})$。

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=45,M=7000000,K=(1<<20)-1;
int n,i,j,l,r,a[N],cf,cg,ans[N];ll cnt[N],S,nxt,need;char tab[65537];
int c[K+8],q[M],p[M];
struct E{
  ll S,v;
  E(){}
  E(ll _S,ll _v){S=_S,v=_v;}
}f[M],g[M];
inline bool cmp(const E&a,const E&b){return a.S<b.S;}
inline void up(int x,int a,ll b){
  if(ans[x]<a)return;
  if(ans[x]==a)cnt[x]+=b;
  else ans[x]=a,cnt[x]=b;
}
inline void merge(){
  int i,j;
  cf=0;
  for(i=0;i<=K;i++)c[i]=0;
  for(i=1;i<=cg;i++)c[g[i].S&K]++;
  for(i=1;i<=K;i++)c[i]+=c[i-1];
  for(i=1;i<=cg;i++)q[c[g[i].S&K]--]=i;
  for(i=0;i<=K;i++)c[i]=0;
  for(i=1;i<=cg;i++)c[g[i].S>>20]++;
  for(i=1;i<=K;i++)c[i]+=c[i-1];
  for(i=cg;i;i--)p[c[g[q[i]].S>>20]--]=q[i];
  for(i=1;i<=cg;i=j){
    int a=M;ll b=0;
    for(j=i;j<=cg&&g[p[i]].S==g[p[j]].S;j++){
      if((g[p[j]].v&1023)<a)a=g[p[j]].v&1023,b=g[p[j]].v>>10;
      else if((g[p[j]].v&1023)==a)b+=g[p[j]].v>>10;
    }
    f[++cf]=E(g[p[i]].S,b<<10|a);
  }
  cg=0;
}
inline int popcount(ll S){return tab[S&65535]+tab[S>>16&65535]+tab[S>>32];}
inline ll fix(ll S){
  return S^(S&need)^(((1LL<<popcount(S&need))-1)<<l);
}
int main(){
  for(i=0;i<65536;i++)tab[i]=__builtin_popcount(i);
  scanf("%d",&n);
  for(i=1;i<=n;i++)scanf("%d",&a[i]),a[i]--;
  f[cf=1]=E(0,1<<10);
  for(i=1;i<=n;i++){
    S=~0ULL>>1;
    for(j=0;j<=a[i];j++)S^=1LL<<j;
    nxt=0;
    for(j=i+1;j<=n;j++)nxt|=1LL<<a[j];
    for(l=a[i];~l;l--)if(nxt>>l&1)break;
    for(r=a[i];r<n;r++)if(nxt>>r&1)break;
    l++,r--;
    need=0;
    for(j=l;j<=r;j++)need|=1LL<<j;
    for(j=1;j<=cf;j++){
      g[++cg]=E(fix(f[j].S),f[j].v);
      g[++cg]=E(fix(f[j].S|(1LL<<a[i])),f[j].v+popcount(S&f[j].S));
    }
    merge();
  }
  for(i=0;i<=n;i++)ans[i]=M;
  for(i=1;i<=cf;i++)up(popcount(f[i].S),f[i].v&1023,f[i].v>>10);
  for(i=1;i<=n;i++)printf("%d %lld\n",ans[i],cnt[i]);
}

　　

Runda 3：

Terytoria [B]

两维独立，考虑一维的情况。

所有区间的交集等于总的减去所有区间的补的并集。将坐标离散化后，枚举一个必然不属于补的并集的位置，那么所有区间的方案都定了，线段树维护并集的大小即可。

时间复杂度$O(n\log n)$。

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=500010,M=2111111;
int n,m,_,X,Y,i,j,x,y,e[N][4],a[N],b[N],c[N<<1],ans;
int gl[N<<1],gr[N<<1],v[N<<1],nxt[N<<1],ed;
int cov[N<<1],mi[M],val[M],tag[M];
inline void add(int&x,int y){v[++ed]=y;nxt[ed]=x;x=ed;}
inline void tag1(int x,int p){mi[x]+=p;tag[x]+=p;}
inline void up(int x){
  if(mi[x<<1]<mi[x<<1|1]){
    mi[x]=mi[x<<1];
    val[x]=val[x<<1];
  }else if(mi[x<<1]>mi[x<<1|1]){
    mi[x]=mi[x<<1|1];
    val[x]=val[x<<1|1];
  }else{
    mi[x]=mi[x<<1];
    val[x]=val[x<<1]+val[x<<1|1];
  }
}
void build(int x,int a,int b){
  tag[x]=0;
  if(a==b){
    mi[x]=cov[a];
    val[x]=c[a+1]-c[a];
    return;
  }
  int mid=(a+b)>>1;
  build(x<<1,a,mid),build(x<<1|1,mid+1,b);
  up(x);
}
void change(int x,int a,int b,int c,int d,int p){
  if(c<=a&&b<=d){tag1(x,p);return;}
  if(tag[x])tag1(x<<1,tag[x]),tag1(x<<1|1,tag[x]),tag[x]=0;
  int mid=(a+b)>>1;
  if(c<=mid)change(x<<1,a,mid,c,d,p);
  if(d>mid)change(x<<1|1,mid+1,b,c,d,p);
  up(x);
}
int solve(int all){
  c[1]=0;
  c[m=2]=all;
  for(i=1;i<=n;i++)c[++m]=a[i],c[++m]=b[i];
  sort(c+1,c+m+1);
  for(_=0,i=1;i<=m;i++)if(i==1||c[i]>c[_])c[++_]=c[i];
  m=_;
  for(i=1;i<=m;i++)gl[i]=gr[i]=cov[i]=0;
  ed=0;
  for(i=1;i<=n;i++){
    x=a[i],y=b[i];
    if(x>y)swap(x,y);
    x=lower_bound(c+1,c+m+1,x)-c;
    y=lower_bound(c+1,c+m+1,y)-c;
    a[i]=x;
    b[i]=y;
    add(gl[x],i);
    add(gr[y],i);
    cov[x]++;
    cov[y]--;
  }
  for(i=1;i<=m;i++)cov[i]+=cov[i-1];
  ans=0;
  build(1,1,m-1);
  for(i=1;i<m;i++){
    for(j=gl[i];j;j=nxt[j]){
      change(1,1,m-1,a[v[j]],b[v[j]]-1,-2);
      change(1,1,m-1,1,m-1,1);
    }
    for(j=gr[i];j;j=nxt[j]){
      change(1,1,m-1,a[v[j]],b[v[j]]-1,2);
      change(1,1,m-1,1,m-1,-1);
    }
    if(!mi[1])ans=max(ans,val[1]);
  }
  return ans;
}
int main(){
  scanf("%d%d%d",&n,&X,&Y);
  for(i=1;i<=n;i++)scanf("%d%d%d%d",&e[i][0],&e[i][1],&e[i][2],&e[i][3]);
  for(i=1;i<=n;i++)a[i]=e[i][0],b[i]=e[i][2];
  int ansx=solve(X);
  for(i=1;i<=n;i++)a[i]=e[i][1],b[i]=e[i][3];
  int ansy=solve(Y);
  printf("%lld",1LL*ansx*ansy);
}

　　

Iloczyny Fibonacciego [A]

令$f_2=1,f_3=2,f_i=f_{i-1}+f_{i-2}(i\geq 4),s_i=f_i+s_{i-4}$。

则对于$x\geq y\geq 2$：

• 如果$y$是偶数，那么$f_xf_y=s_{x+y-2}+f_{x-y+2}-s_{x-y+2}$。
• 如果$y$是奇数且$x\neq y$，那么$f_xf_y=s_{x+y-2}+f_{x-y+4}-s_{x-y+4}+f_{x-y+1}$。
• 如果$y$是奇数且$x=y$，那么$f_xf_y=s_{x+y-2}+f_{x-y+4}-s_{x-y+4}+f_{2}$。

首先处理掉$x=y$的贡献，容易发现剩下的贡献只和$y$的奇偶性以及$x-y$和$x+y$有关，构造多项式卷积利用NTT求出贡献即可。

那么剩下的问题就是将$\sum a_if_i$的$a$转化成合法的斐波那契表示。

分治，设$solve(l,r)$表示$\sum_{i=l}^r a_if_i$的斐波那契表示，如果将前导0和后缀0都去掉的话，那么它的长度不超过$O(r-l+\log n)$。

• 若$l<r$，取$mid=\lfloor\frac{l+r}{2}\rfloor$，则$solve(l,r)=solve(l,mid)+solve(mid+1,r)$，而斐波那契进制的加法可以在线性时间内完成。
• 若$l=r$，则可以利用$(f_{x-2}+f_{x})f_l=f(l-x)+f(l+x)$（$x$是偶数）将$a_l$拆成$O(\log n)$个互不相邻的$2$，然后用斐波那契进制的加法将其修正为合法的斐波那契表示；需要注意的是如果$l$太小以至$l-x$越界的话，这时$a_lf_l$的数值一定不大，可以暴力分解为斐波那契表示。

时间复杂度$T(n)=2T(\frac{n}{2})+O(n+\log n)=O(n\log n)$。

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<string>
using namespace std;
typedef long long ll;
typedef pair<int,string>E;
const int N=2111111;
int Case,lenx,leny,n,i,x,k,a[N],b[N],A[N],B[N],C[N];ll f[N],s[N];E fin;
typedef unsigned int uint32;
typedef long long int64;
typedef unsigned long long uint64;
typedef uint32 word;
typedef uint64 dword;
typedef int sword;
const int word_bits=sizeof(word)*8;
word mod,Modinv,r2;
struct UnsafeMod{
  word x;
  UnsafeMod(): x(0) {}
  UnsafeMod(word _x): x(init(_x)) {}
  UnsafeMod& operator += (const UnsafeMod& rhs) {
    (x += rhs.x) >= mod && (x -= mod);
    return *this;
  }
  UnsafeMod& operator -= (const UnsafeMod& rhs) {
    sword(x -= rhs.x) < 0 && (x += mod);
    return *this;
  }
  UnsafeMod& operator *= (const UnsafeMod& rhs) {
    x = reduce(dword(x) * rhs.x);
    return *this;
  }
  UnsafeMod operator + (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) += rhs;
  }
  UnsafeMod operator - (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) -= rhs;
  }
  UnsafeMod operator * (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) *= rhs;
  }
  UnsafeMod pow(uint64 e) const {
    UnsafeMod ret(1);
    for (UnsafeMod base = *this; e; e >>= 1, base *= base) {
      if (e & 1) ret *= base;
    }
    return ret;
  }
  word get() const {
    return reduce(x);
  }
  static word modulus() {
    return mod;
  }
  static word init(word w) {
    return reduce(dword(w) * r2);
  }
  static void set_mod(word m) {
    mod = m;
    Modinv = mul_inv(mod);
    r2 = -dword(mod) % mod;
  }
  static word reduce(dword x) {
    word y = word(x >> word_bits) - word((dword(word(x) * Modinv) * mod) >> word_bits);
    return sword(y) < 0 ? y + mod : y;
  }
  static word mul_inv(word n, int e = 6, word x = 1) {
    return !e ? x : mul_inv(n, e - 1, x * (2 - x * n));
  }
}pool[N];
namespace NTT{
const int N=1048576*2,K=20,P=998244353,G=3;
UnsafeMod A[N+10],B[N+10],C[N+10];
UnsafeMod g[K+1],ng[K+10],gw[N+10],ngw[N+10];
int pos[N+10],inv[N+10];
inline void doNTT(UnsafeMod*a,int n,int t){
  for(int i=1;i<n;i++)if(i<pos[i])swap(a[i],a[pos[i]]);
  for(int d=0;(1<<d)<n;d++){
    int m=1<<d,m2=m<<1;
    UnsafeMod*_w=t==1?gw:ngw;
    _w+=m;
    for(int i=0;i<n;i+=m2){
      UnsafeMod*w=_w;
      for(int j=i;j<m+i;j++,w++){
        UnsafeMod t=*w*a[j+m];
        a[j+m]=a[j]-t;
        a[j]+=t;
      }
    }
  }
  if(t==-1){
    UnsafeMod j=inv[n];
    for(int i=0;i<n;i++)a[i]*=j;
  }
};
void trans(int k,int*a,UnsafeMod*A){
  int i;
  for(i=0;i<k;i++)A[i]=a[i];
  doNTT(A,k,1);
}
void mul(int k,int*a,UnsafeMod*B,int*c){
  int i;
  for(i=0;i<k;i++)A[i]=a[i];
  doNTT(A,k,1);
  for(i=0;i<k;i++)C[i]=A[i]*B[i];
  doNTT(C,k,-1);
  for(i=0;i<k;i++)c[i]=C[i].get();
}
void pre(){
  int i,j;
  UnsafeMod::set_mod(P);
  for(g[K]=((UnsafeMod)G).pow((P-1)/N),ng[K]=g[K].pow(P-2),i=K-1;~i;i--)g[i]=g[i+1]*g[i+1],ng[i]=ng[i+1]*ng[i+1];
  for(i=0;i<=K;i++){
    gw[1<<i]=ngw[1<<i]=1;
    for(j=1;j<1<<i;j++){
      gw[(1<<i)+j]=gw[(1<<i)+j-1]*g[i];
      ngw[(1<<i)+j]=ngw[(1<<i)+j-1]*ng[i];
    }
  }
  for(inv[1]=1,i=2;i<=N;i++)inv[i]=1LL*(P-inv[P%i])*(P/i)%P;
}
void init(int k){
  int i,j;
  j=__builtin_ctz(k)-1;
  for(i=0;i<k;i++)pos[i]=pos[i>>1]>>1|((i&1)<<j);
}
}
namespace FIB{
const int M=100;
int n=90,m,a[M];ll b[M],f[M];
int q[N],len,L;
void init(){
  for(f[0]=f[1]=1,i=2;i<=n;i++)f[i]=f[i-1]+f[i-2];
  for(i=2;i<=n;i+=2){
    a[++m]=i;
    b[m]=f[i-2]+f[i];
  }
  for(f[1]=f[2]=1,i=3;i<=n;i++)f[i]=f[i-1]+f[i-2];
}
inline void add(int x,int y){
  x-=L;
  while(len<=x)q[len++]=0;
  q[x]+=y;
}
inline void up(int x){for(;q[x]&&q[x+1];x+=2)q[x]--,q[x+1]--,q[x+2]++;}
inline E fix(){
  int i;
  for(i=0;i<5;i++)q[len++]=0;
  int t=min(L-1,5);
  if(L-t==2)t++;
  len+=t;
  L-=t;
  for(i=len-1;i>=t;i--)q[i]=q[i-t];
  for(;~i;i--)q[i]=0;
  for(i=len-1;i;i--){
    if(q[i]==3)q[i]=0,q[i+2]++,up(i+2),q[i-2]++,up(i-3);
    else if(q[i]==2){
      if(q[i-1])q[i]=0,q[i-1]--,q[i+2]++,up(i+2);
      else q[i]=0,q[i+1]++,up(i+1),q[i-2]++,up(i-3);
    }else up(i-1);
  }
  if(L==1)q[1]+=q[0],q[0]=0;
  while(!q[len-1])len--;
  for(t=0;!q[t];t++,L++);
  E ret(L,string(len-t,0));
  for(i=t;i<len;i++)ret.second[i-t]=q[i];
  return ret;
}
inline E single(int A,ll B){
  if(!B)return E(0,"");
  if(B==1)return E(A,string(1,1));
  int x=m,i;
  while(x&&b[x]>B)x--;
  if(A-a[x]<2){
    B*=f[A];
    L=2;
    len=0;
    for(x=n;x>=2;x--)if(B>=f[x])add(x,1),B-=f[x];
    E ret(L,string(len,0));
    for(i=0;i<len;i++)ret.second[i]=q[i];
    return ret;
  }
  L=A-a[x];
  len=0;
  for(;x;x--)while(B>=b[x]){
    add(A-a[x],1);
    add(A+a[x],1);
    B-=b[x];
  }
  add(A,B);
  return fix();
}
inline E merge(const E&A,const E&B){
  if(!A.first)return B;
  if(!B.first)return A;
  L=min(A.first,B.first);
  len=0;
  for(int i=0;i<A.second.size();i++)add(A.first+i,A.second[i]);
  for(int i=0;i<B.second.size();i++)add(B.first+i,B.second[i]);
  return fix();
}
}
void read(int&len,int*a){
  scanf("%d",&len);
  len++;
  a[1]=0;
  for(int i=2;i<=len;i++)scanf("%d",&a[i]);
}
E solve(int l,int r){
  if(l==r)return FIB::single(l,f[l]);
  int mid=(l+r)>>1;
  return FIB::merge(solve(l,mid),solve(mid+1,r));
}
int main(){
  NTT::pre();
  FIB::init();
  scanf("%d",&Case);
  while(Case--){
    read(lenx,a);
    read(leny,b);
    for(k=1;k<=lenx+leny;k<<=1);
    NTT::init(k);
    for(i=0;i<k;i++)A[i]=B[i]=f[i]=s[i]=0;
    for(i=2;i<=lenx;i++)A[i]=a[i];
    for(i=2;i<=leny;i++)B[i]=b[i];
    NTT::trans(k,A,pool);
    NTT::mul(k,B,pool,C);
    for(i=2;i<k;i++)s[i-2]+=C[i];
    for(i=3;i<=lenx&&i<=leny;i+=2)if(a[i]&&b[i])f[2]++;
    for(i=0;i<k;i++)A[i]=B[i]=0;
    for(i=2;i<=lenx;i+=2)A[i]=a[i];
    for(i=2;i<=leny;i++)B[leny-i]=b[i];
    NTT::trans(k,B,pool);
    NTT::mul(k,A,pool,C);
    for(i=0;i<k;i++)if(C[i]&&i<leny){
      x=leny-i;
      f[x+2]+=C[i];
      s[x+2]-=C[i];
    }
    for(i=0;i<k;i++)A[i]=0;
    for(i=3;i<=lenx;i+=2)A[i]=a[i];
    NTT::mul(k,A,pool,C);
    for(i=0;i<k;i++)if(C[i]&&i<leny){
      x=leny-i;
      f[x+4]+=C[i];
      s[x+4]-=C[i];
      f[x+1]+=C[i];
    }
    for(i=0;i<k;i++)A[i]=B[i]=0;
    for(i=2;i<=lenx;i++)A[i]=a[i];
    for(i=2;i<=leny;i+=2)B[leny-i]=b[i];
    NTT::trans(k,A,pool);
    NTT::mul(k,B,pool,C);
    for(i=0;i<k;i++)if(C[i]&&i>leny){
      x=i-leny;
      f[x+2]+=C[i];
      s[x+2]-=C[i];
    }
    for(i=0;i<k;i++)B[i]=0;
    for(i=3;i<=leny;i+=2)B[leny-i]=b[i];
    NTT::mul(k,B,pool,C);
    for(i=0;i<k;i++)if(C[i]&&i>leny){
      x=i-leny;
      f[x+4]+=C[i];
      s[x+4]-=C[i];
      f[x+1]+=C[i];
    }
    for(i=k-1;i>=4;i--)s[i-4]+=s[i];
    for(i=0;i<k;i++)f[i]+=s[i];
    n=k-1;
    while(!f[n])n--;
    fin=solve(2,n);
    printf("%d",fin.first+fin.second.size()-2);
    for(i=2;i<fin.first;i++)printf(" 0");
    for(i=0;i<fin.second.size();i++)printf(" %d",(int)fin.second[i]);
    puts("");
  }
}

　　

Runda 4：

Szprotki i szczupaki [B]

显然最优策略是每次吃能吃的最大的数。

离散化后建立权值线段树，对于每个询问暴力模拟，每次在线段树上二分找出一段要吃掉的后缀，使得吃掉它们之后可以解锁下一个数或者达到最终目标。容易发现每次解锁都会使得我方的重量翻倍，因此最多只有$O(\log w)$次迭代。

因为每个询问独立，因此需要在每次清空一个区间后将其保存下来，方便询问结束后还原。

时间复杂度$O(q\log n\log w)$。

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=400010,M=1111111;
const ll inf=1LL<<60;
int n,m,q,i,x,ce,have[N];
ll a[N],e[N],op[N][3];
int POS,vis[M];ll cnt[M],sum[M];
int C;ll NXT,SUM,CNT;
int pool[M],cp;
ll sc[M],ss[M];
inline void up(int x){
  cnt[x]=cnt[x<<1]+cnt[x<<1|1];
  sum[x]=sum[x<<1]+sum[x<<1|1];
}
void build(int x,int a,int b){
  if(a==b){
    cnt[x]=have[a];
    sum[x]=cnt[x]*e[a];
    return;
  }
  int mid=(a+b)>>1;
  build(x<<1,a,mid),build(x<<1|1,mid+1,b);
  up(x);
}
void change(int x,int a,int b,int c,ll A,ll B){
  sum[x]+=A;
  cnt[x]+=B;
  if(a==b)return;
  int mid=(a+b)>>1;
  if(c<=mid)change(x<<1,a,mid,c,A,B);else change(x<<1|1,mid+1,b,c,A,B);
}
void getnxt(int x,int a,int b){
  if(NXT)return;
  if(!cnt[x])return;
  if(a==b){
    NXT=e[a];
    return;
  }
  int mid=(a+b)>>1;
  if(C<=mid)getnxt(x<<1,a,mid);
  getnxt(x<<1|1,mid+1,b);
}
void eat(int x,int a,int b){
  if(vis[x]<POS){
    vis[x]=POS;
    pool[++cp]=x;
    sc[x]=cnt[x];
    ss[x]=sum[x];
  }
  if(SUM>NXT)return;
  if(!cnt[x])return;
  if(b<=C){
    if(SUM+sum[x]<=NXT){
      SUM+=sum[x];
      CNT+=cnt[x];
      cnt[x]=sum[x]=0;
      return;
    }
    if(a==b){
      ll tmp=(NXT-SUM)/e[a];
      while(tmp*e[a]+SUM<=NXT)tmp++;
      ll val=tmp*e[a];
      cnt[x]-=tmp,sum[x]-=val;
      SUM+=val;
      CNT+=tmp;
      return;
    }
  }
  int mid=(a+b)>>1;
  if(C>mid)eat(x<<1|1,mid+1,b);
  eat(x<<1,a,mid);
  up(x);
}
inline int lower(ll x){
  int l=1,r=m,t,mid;
  while(l<=r)if(e[mid=(l+r)>>1]>=x)r=(t=mid)-1;else l=mid+1;
  return t;
}
inline int query(ll A,ll B){
  int ans=0;
  cp=0;
  while(A<B){
    C=lower(A);
    NXT=0;
    getnxt(1,1,m);
    NXT=min(NXT,B-1);
    C--;
    SUM=A;
    CNT=0;
    eat(1,1,m);
    if(SUM<=NXT)return -1;
    A=SUM;
    ans+=CNT;
  }
  return ans;
}
int main(){
  scanf("%d",&n);
  e[ce=1]=0;
  for(i=1;i<=n;i++)scanf("%lld",&a[i]),e[++ce]=a[i];
  scanf("%d",&q);
  for(i=1;i<=q;i++){
    scanf("%lld%lld",&op[i][0],&op[i][1]);
    if(op[i][0]==1)scanf("%lld",&op[i][2]);
    if(op[i][0]==2)e[++ce]=op[i][1];
  }
  sort(e+1,e+ce+1);
  for(i=1;i<=ce;i++)if(i==1||e[i]>e[m])e[++m]=e[i];
  e[++m]=inf;
  have[m]=1;
  for(i=1;i<=n;i++)have[lower_bound(e+1,e+m+1,a[i])-e]++;
  build(1,1,m);
  for(i=1;i<=q;i++){
    POS++;
    if(op[i][0]==1){
      printf("%d\n",query(op[i][1],op[i][2]));
      while(cp){
        x=pool[cp--];
        cnt[x]=sc[x];
        sum[x]=ss[x];
      }
    }
    if(op[i][0]==2)change(1,1,m,lower_bound(e+1,e+m+1,op[i][1])-e,op[i][1],1);
    if(op[i][0]==3)change(1,1,m,lower_bound(e+1,e+m+1,op[i][1])-e,-op[i][1],-1);
  }
}

　　

Wyspa [A]

首先将不能被任何一个湖边点到达的海边点删除。因为是平面图，所以每个湖边点能到达的海边点都是环上一个区间，也就是序列上不超过两个区间，可以缩SCC后在$O(n\log n)$的时间内递推求出这个范围。

那么问题转化为给定环上一些区间，求选点的方案数使得每个区间内至少选了一个点。

如果区间$A$包含$B$，那么满足$B$一定可以满足$A$，可以将$A$删除。同时我们可以离散化区间的左右端点使得点数和区间数同阶。通过旋转一个区间到$[1,len]$，我们可以发现从左往右选的第一个点一定在$[1,len]$范围内，枚举第一个选的点，那么跨过$1$和$n$的区间都可以视作序列上的正常区间，达到破环成链的目的。

动态规划，设$f_i$表示考虑了前$i$个点，$i$点必选的方案数，则$f_i=\sum f_j$，其中$[j+1,i-1]$不能含有完整的区间，令$g_i$表示右端点不超过$i$的区间中左端点的最大值，则$j\geq g_{i-1}$，可以利用前缀和$O(1)$转移。

如果将最短的区间旋转到$[1,len]$的话，则时间复杂度为$O(\min(len)\times cnt)$，其中$cnt$为区间数，因为平面图的限制这个乘积是$O(n)$级别的。

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=500010,M=2000010,P=1000000007;
int n,m,ca,cb,cnt,i,j,k,x,y,scc,base=1;
bool vis[N];
int ed,g[N],v[M],nxt[M],G[N],V[M],NXT[M];
int id[N],at[N],q[N],t;
int pool[N],st[N],en[N],cp,last[N];
int ce;
struct Info{int a,b,c,d;}f[N];
struct E{int l,r;E(){}E(int _l,int _r){l=_l,r=_r;}}e[N<<1];
inline bool cmp(const E&a,const E&b){return a.l<b.l;}
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
inline void readch(char&a){while(!(((a=getchar())=='-')||(a=='>')));}
inline void umin(int&a,int b){a>b?(a=b):0;}
inline void umax(int&a,int b){a<b?(a=b):0;}
inline void add(int x,int y){
  v[++ed]=y;nxt[ed]=g[x];g[x]=ed;
  V[ed]=x;NXT[ed]=G[y];G[y]=ed;
}
void dfs(int x){
  if(vis[x])return;
  vis[x]=1;
  for(int i=g[x];i;i=nxt[i])dfs(v[i]);
}
void dfs1(int x){
  if(vis[x])return;
  vis[x]=1;
  for(int i=g[x];i;i=nxt[i])dfs1(v[i]);
  q[++t]=x;
}
void dfs2(int x){
  if(!vis[x])return;
  vis[x]=0;
  at[x]=scc;
  pool[++cp]=x;
  for(int i=G[x];i;i=NXT[i])dfs2(V[i]);
}
inline void ext(int o,int x,int y){
  if(!x)return;
  if(!f[o].a)f[o].a=x,f[o].b=y;
  else if(!f[o].c)f[o].c=x,f[o].d=y;
  else puts("GG");
}
namespace COUNTING{
typedef unsigned int uint32;
typedef long long int64;
typedef unsigned long long uint64;
typedef uint32 word;
typedef uint64 dword;
typedef int sword;
const int word_bits=sizeof(word)*8;
word mod,Modinv,r2;
struct UnsafeMod{
  word x;
  UnsafeMod(): x(0) {}
  UnsafeMod(word _x): x(init(_x)) {}
  UnsafeMod& operator += (const UnsafeMod& rhs) {
    (x += rhs.x) >= mod && (x -= mod);
    return *this;
  }
  UnsafeMod& operator -= (const UnsafeMod& rhs) {
    sword(x -= rhs.x) < 0 && (x += mod);
    return *this;
  }
  UnsafeMod& operator *= (const UnsafeMod& rhs) {
    x = reduce(dword(x) * rhs.x);
    return *this;
  }
  UnsafeMod operator + (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) += rhs;
  }
  UnsafeMod operator - (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) -= rhs;
  }
  UnsafeMod operator * (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) *= rhs;
  }
  UnsafeMod pow(uint64 e) const {
    UnsafeMod ret(1);
    for (UnsafeMod base = *this; e; e >>= 1, base *= base) {
      if (e & 1) ret *= base;
    }
    return ret;
  }
  word get() const {
    return reduce(x);
  }
  static word modulus() {
    return mod;
  }
  static word init(word w) {
    return reduce(dword(w) * r2);
  }
  static void set_mod(word m) {
    mod = m;
    Modinv = mul_inv(mod);
    r2 = -dword(mod) % mod;
  }
  static word reduce(dword x) {
    word y = word(x >> word_bits) - word((dword(word(x) * Modinv) * mod) >> word_bits);
    return sword(y) < 0 ? y + mod : y;
  }
  static word mul_inv(word n, int e = 6, word x = 1) {
    return !e ? x : mul_inv(n, e - 1, x * (2 - x * n));
  }
}dp[N],v[N],ans;
int n,m,_,ca,i,j,k,x,y,e[N][2],is[N],a[N];
int p[N],val[N];
int minlen,S,now,en;
int g[N],q[N][2],h,t;
int f[N<<1],lim[N];
inline void init(int A,int B,int C,int D){
  if(!C){
    e[++m][0]=A;
    e[m][1]=B;
    umax(f[B],A);
    umax(f[B+n],A+n);
  }else{
    e[++m][0]=C;
    e[m][1]=B;
    umax(f[B+n],C);
  }
}
inline void add(int l,int r){
  if(l<=r){
    if(f[r]>l)return;
    is[l-1]=is[r]=1;
  }else{
    if(f[r+n]>l)return;
    is[l-1]=is[r]=is[n]=1;
  }
  e[++_][0]=l;
  e[_][1]=r;
}
inline void ins(int x,int y){
  if(h<=t&&q[t][1]>=y)return;
  q[++t][0]=x;
  q[t][1]=y;
}
inline int askmin(int x){
  while(h<=t&&q[h][1]<=x)h++;
  if(h>t)return n;
  return q[h][0];
}
inline void cal(int lim,int n){
  for(int i=1;i<=n;i++){
    dp[i]=dp[i-1];
    if(f[i-1])dp[i]-=dp[f[i-1]-1];
    if(i<=lim)dp[i]+=1;
    dp[i]=dp[i]*v[i]+dp[i-1];
  }
}
int solve(){
  UnsafeMod::set_mod(P);
  for(i=1;i<=n+n;i++)umax(f[i],f[i-1]);
  for(i=1;i<=m;i++)add(e[i][0],e[i][1]);
  m=_;
  for(p[0]=i=1;i<=n;i++)p[i]=p[i-1]*2%P;
  for(i=0;i<=n;i++)p[i]--;
  is[n]=1;
  for(i=1;i<=n;i++)if(is[i])a[is[i]=++ca]=i;
  for(i=n;i;i--)if(!is[i])is[i]=is[i+1];
  n=ca;
  for(i=1;i<=n;i++)val[i]=p[a[i]-a[i-1]];
  minlen=n,S=1;
  for(i=1;i<=m;i++){
    x=is[e[i][0]],y=is[e[i][1]];
    if(x<=y)now=y-x+1;else now=y-x+1+n;
    if(now<=minlen)minlen=now,S=x;
  }
  for(i=1,j=S;i<=n;i++){
    v[i]=val[j];
    j++;
    if(j>n)j=1;
  }
  en=n;
  for(i=0;i<=n+1;i++)f[i]=0;
  for(i=1;i<=m;i++){
    x=is[e[i][0]],y=is[e[i][1]];
    if(y<x)y+=n;
    y=y-x;
    while(1){
      if(S<=x&&x<S+n)break;
      x+=n;
    }
    x-=S-1;
    if(y==n-1)x=1,y=n;else y+=x;
    if(y>n)y-=n;
    if(x<=y){
      umax(f[y],x);
      umin(en,y);
    }else{
      umax(g[y+1],x);
    }
  }
  for(i=1;i<=n;i++)umax(f[i],f[i-1]);
  h=1,t=0;
  for(i=1;i<=n;i++){
    now=en;
    if(g[i])ins(i-1,g[i]);
    umin(now,askmin(i));
    lim[i]=now;
  }
  for(i=max(f[n],1);i<=n;i=j){
    for(j=i;j<=n&&lim[i]==lim[j];j++);
    cal(lim[i],j-1);
    ans+=dp[j-1]-dp[i-1];
  }
  return ans.get();
}
}
int main(){
  read(n);read(m);read(ca);read(cb);
  while(m--){
    char ch;
    read(x);
    readch(ch);
    readch(ch);
    read(y);
    add(x,y);
    if(ch=='-')add(y,x);
  }
  for(i=1;i<=ca;i++)dfs(i);
  for(i=ca+1;i<=ca+cb;i++)if(vis[i])id[i]=++cnt;else base=base*2%P;
  for(i=1;i<=n;i++)vis[i]=0;
  for(i=1;i<=n;i++)if(!vis[i])dfs1(i);
  for(i=t;i;i--)if(vis[q[i]]){
    scc++;
    st[scc]=cp+1;
    dfs2(q[i]);
    en[scc]=cp;
  }
  for(i=scc;i;i--){
    ce=0;
    for(j=st[i];j<=en[i];j++){
      x=pool[j];
      if(id[x])e[++ce]=E(id[x],id[x]);
      for(k=g[x];k;k=nxt[k]){
        y=at[v[k]];
        if(y==i)continue;
        if(last[y]==i)continue;
        last[y]=i;
        if(f[y].a)e[++ce]=E(f[y].a,f[y].b);
        if(f[y].c)e[++ce]=E(f[y].c,f[y].d);
      }
    }
    if(!ce)continue;
    sort(e+1,e+ce+1,cmp);
    x=0,y=-1;
    for(j=1;j<=ce;j++){
      if(e[j].l>y+1){
        ext(i,x,y);
        x=e[j].l;
      }
      umax(y,e[j].r);
    }
    ext(i,x,y);
  }
  COUNTING::n=cnt;
  for(i=1;i<=ca;i++){
    x=at[i];
    if(f[x].a){
      COUNTING::init(f[x].a,f[x].b,f[x].c,f[x].d);
      f[x].a=0;
    }
  }
  base=1LL*base*COUNTING::solve()%P;
  printf("%d",base);
}

　　

Runda 5：

Trzy kule [B]

答案为必然满足一个条件的方案数$-$必然满足两个条件的方案数$+$必然满足三个条件的方案数。

一个和两个的情况比较简单，可以枚举相同的位数利用组合数在$O(n)$时间内得到答案。

对于三个的情况，不妨令第一个串为全0，那么对于每一位，一共有4种情况：000，001，010，011。

令这四种情况的数量分别为$A,B,C,D$，这些位在要求的串中为1的数量分别为$a,b,c,d$，则有：

• $a+b+c+d\leq r_1$
• $a+b+C-c+D-d\leq r_2$
• $a+B-b+c+D-d\leq r_3$

即

• $c+d\leq r_1-a-b$
• $c+d\geq a+b+C-r_2+D$
• $c-d\leq r_3-a-B+b-D$

枚举$a$和$b$后，则对应的$c$和$d$是关于$c+d$和$c-d$的二维数点，二维前缀和即可。

时间复杂度$O(n^2)$。

#include<cstdio>
const int N=10005,P=1000000007;
typedef unsigned int uint32;
typedef long long int64;
typedef unsigned long long uint64;
typedef uint32 word;
typedef uint64 dword;
typedef int sword;
const int word_bits=sizeof(word)*8;
word mod,Modinv,r2;
struct UnsafeMod{
  word x;
  UnsafeMod(): x(0) {}
  UnsafeMod(word _x): x(init(_x)) {}
  UnsafeMod& operator += (const UnsafeMod& rhs) {
    (x += rhs.x) >= mod && (x -= mod);
    return *this;
  }
  UnsafeMod& operator -= (const UnsafeMod& rhs) {
    sword(x -= rhs.x) < 0 && (x += mod);
    return *this;
  }
  UnsafeMod& operator *= (const UnsafeMod& rhs) {
    x = reduce(dword(x) * rhs.x);
    return *this;
  }
  UnsafeMod operator + (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) += rhs;
  }
  UnsafeMod operator - (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) -= rhs;
  }
  UnsafeMod operator * (const UnsafeMod &rhs) const {
    return UnsafeMod(*this) *= rhs;
  }
  UnsafeMod pow(uint64 e) const {
    UnsafeMod ret(1);
    for (UnsafeMod base = *this; e; e >>= 1, base *= base) {
      if (e & 1) ret *= base;
    }
    return ret;
  }
  word get() const {
    return reduce(x);
  }
  static word modulus() {
    return mod;
  }
  static word init(word w) {
    return reduce(dword(w) * r2);
  }
  static void set_mod(word m) {
    mod = m;
    Modinv = mul_inv(mod);
    r2 = -dword(mod) % mod;
  }
  static word reduce(dword x) {
    word y = word(x >> word_bits) - word((dword(word(x) * Modinv) * mod) >> word_bits);
    return sword(y) < 0 ? y + mod : y;
  }
  static word mul_inv(word n, int e = 6, word x = 1) {
    return !e ? x : mul_inv(n, e - 1, x * (2 - x * n));
  }
}ans,f[N],g[N],s[N][N];
int n,i,lim[3],fac[N],inv[N];char a[3][N];
inline UnsafeMod getC(int n,int m){
  if(n<m)return 0;
  UnsafeMod ret=fac[n];
  ret*=inv[m];
  return ret*inv[n-m];
}
void pre(int n,UnsafeMod*f){for(int i=0;i<N;i++)f[i]=getC(n,i);}
UnsafeMod one(int x){
  UnsafeMod ret=0;
  for(int i=0;i<=lim[x];i++)ret+=getC(n,i);
  return ret;
}
UnsafeMod two(int x,int y){
  UnsafeMod ret=0;
  int cnt=0,i,j;
  for(i=0;i<n;i++)if(a[x][i]==a[y][i])cnt++;
  pre(cnt,f);
  pre(n-cnt,g);
  for(i=0;i<=cnt;i++)for(j=0;j<=n-cnt;j++){
    if(i+j>lim[x])break;
    if(i+n-cnt-j>lim[y])continue;
    ret+=f[i]*g[j];
  }
  return ret;
}
UnsafeMod three(){
  UnsafeMod ret=0;
  int i,j,A=0,B=0,C=0,D=0,ra=lim[0],rb=lim[1],rc=lim[2];
  for(i=0;i<n;i++){
    int x=a[0][i]-'0',y=a[1][i]-'0',z=a[2][i]-'0';
    y^=x,z^=x;
    if(y==0&&z==0)A++;
    if(y==0&&z==1)B++;
    if(y==1&&z==0)C++;
    if(y==1&&z==1)D++;
  }
  pre(C,f),pre(D,g);
  for(i=0;i<=C;i++)for(j=0;j<=D;j++)s[i+j][i-j+D]+=f[i]*g[j];
  int m=C+D;
  for(i=0;i<=m;i++)for(j=0;j<=m;j++){
    if(i)s[i][j]+=s[i-1][j];
    if(j)s[i][j]+=s[i][j-1];
    if(i&&j)s[i][j]-=s[i-1][j-1];
  }
  pre(A,f),pre(B,g);
  for(i=0;i<=A;i++)for(j=0;j<=B&&i+j<=ra;j++){
    int l=i+j+C+D-rb;
    int r=ra-i-j;
    if(l<0)l=0;
    if(r>m)r=m;
    if(l>r)continue;
    int k=rc-i+j-B;
    if(k<0)continue;
    if(k>m)k=m;
    UnsafeMod tmp=s[r][k];
    if(l)tmp-=s[l-1][k];
    ret+=tmp*f[i]*g[j];
  }
  return ret;
}
int main(){
  UnsafeMod::set_mod(P);
  scanf("%d",&n);
  for(i=0;i<3;i++)scanf("%d%s",&lim[i],a[i]);
  for(fac[0]=i=1;i<=n;i++)fac[i]=1LL*fac[i-1]*i%P;
  for(inv[0]=inv[1]=1,i=2;i<=n;i++)inv[i]=1LL*(P-inv[P%i])*(P/i)%P;
  for(i=2;i<=n;i++)inv[i]=1LL*inv[i-1]*inv[i]%P;
  ans=one(0)+one(1)+one(2)-two(0,1)-two(0,2)-two(1,2)+three();
  printf("%u",ans.get());
}

　　

Osady i warownie 2 [B]

考虑两种最极端的从左上角到右下角的路径：尽量优先往右走，不能走时再往下走的路径和尽量优先往下走，不能走时再往右走的路径。如果两条路径的边界接触到了对方，那么不存在合法的路径，否则存在。如下图黄线和蓝线所示：

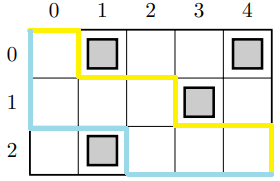
线段树维护这两条路径，对于每个障碍$(r,c)$：

• 如果$(r,c)$是起点或者终点，那么显然。
• 否则如果它严格在黄线之上或者严格在蓝线之下，那么可以忽略。
• 否则如果它同时接触到了黄线和蓝线，那么它会将黄线和蓝线连通，使得起点和终点不连通。
• 否则如果它既没有接触到黄线，也没有接触到蓝线，那么将其放在池子里，暂时不会影响结果。
• 否则如果它接触到了蓝线或者黄线，那么它的加入会导致蓝线或者黄线的扩张，在不断迭代扩张的过程中从池子里找出和线接触的障碍，用其继续扩张线。在这里可以对于每一行和每一列用std::set存储有哪些待定障碍。

时间复杂度$O(k\log n)$。

#include<cstdio>
#include<algorithm>
#include<set>
using namespace std;
const int N=100010,M=262150;
int n,m,_,x,y,z,last,pos[N],mi[M],ma[M];
int q[5555555][2],h,t;
set<int>row[N],col[N];
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
inline void umin(int&a,int b){a>b?(a=b):0;}
inline void umax(int&a,int b){a<b?(a=b):0;}
void build(int x,int a,int b){
  if(a==b){
    pos[a]=x;
    mi[x]=n+1;
    ma[x]=0;
    if(a==0)mi[x]=0;
    if(a==m+1)ma[x]=n+1;
    return;
  }
  int mid=(a+b)>>1;
  build(x<<1,a,mid),build(x<<1|1,mid+1,b);
  mi[x]=min(mi[x<<1],mi[x<<1|1]);
  ma[x]=max(ma[x<<1],ma[x<<1|1]);
}
int askmin(int x,int a,int b,int c,int d){
  if(c<=a&&b<=d)return mi[x];
  int mid=(a+b)>>1,t=N;
  if(c<=mid)t=askmin(x<<1,a,mid,c,d);
  if(d>mid)umin(t,askmin(x<<1|1,mid+1,b,c,d));
  return t;
}
int askmax(int x,int a,int b,int c,int d){
  if(c<=a&&b<=d)return ma[x];
  int mid=(a+b)>>1,t=0;
  if(c<=mid)t=askmax(x<<1,a,mid,c,d);
  if(d>mid)umax(t,askmax(x<<1|1,mid+1,b,c,d));
  return t;
}
inline void changemin(int x,int p){for(x=pos[x];x;x>>=1)umin(mi[x],p);}
inline void changemax(int x,int p){for(x=pos[x];x;x>>=1)umax(ma[x],p);}
inline int checkS(int y,int x){
  int t=askmin(1,0,m+1,x,m+1);
  if(t<=y)return -1;
  if(t==y+1||askmin(1,0,m+1,x-1,m+1)<=y+1)return 0;
  return 1;
}
inline int checkT(int y,int x){
  int t=askmax(1,0,m+1,0,x);
  if(t>=y)return -1;
  if(t==y-1||askmax(1,0,m+1,0,x+1)>=y-1)return 0;
  return 1;
}
inline void extS(int x,int y){
  q[h=t=1][0]=x;
  q[1][1]=y;
  while(h<=t){
    x=q[h][0];
    y=q[h++][1];
    changemin(y,x);
    while(row[x-1].size()){
      set<int>::iterator it=row[x-1].begin();
      if((*it)<=y+1){
        q[++t][0]=x-1;
        q[t][1]=*it;
        row[x-1].erase(*it);
      }else break;
    }
    while(col[y+1].size()){
      set<int>::reverse_iterator it=col[y+1].rbegin();
      if((*it)>=x-1){
        q[++t][0]=*it;
        q[t][1]=y+1;
        col[y+1].erase(*it);
      }else break;
    }
  }
}
inline void extT(int x,int y){
  q[h=t=1][0]=x;
  q[1][1]=y;
  while(h<=t){
    x=q[h][0];
    y=q[h++][1];
    changemax(y,x);
    while(row[x+1].size()){
      set<int>::reverse_iterator it=row[x+1].rbegin();
      if((*it)>=y-1){
        q[++t][0]=x+1;
        q[t][1]=*it;
        row[x+1].erase(*it);
      }else break;
    }
    while(col[y-1].size()){
      set<int>::iterator it=col[y-1].begin();
      if((*it)<=x+1){
        q[++t][0]=*it;
        q[t][1]=y-1;
        col[y-1].erase(*it);
      }else break;
    }
  }
}
inline bool merge(int x,int y){
  x++,y++;
  if(x==1&&y==1)return 1;
  if(x==n&&y==m)return 1;
  int A=checkS(x,y);
  if(A<0)return 0;
  int B=checkT(x,y);
  if(B<0)return 0;
  if(A==0&&B==0)return 1;
  if(A==1&&B==1){
    row[x].insert(y);
    col[y].insert(x);
  }
  if(A==0)extS(x,y);
  if(B==0)extT(x,y);
  return 0;
}
int main(){
  read(n),read(m),read(_);
  build(1,0,m+1);
  while(_--){
    read(x),read(y),read(z);
    x=(x^last)%n;
    y=(y^last)%m;
    if(merge(x,y))puts("TAK"),last^=z;else puts("NIE");
  }
}

　　

Podatki drogowe [A]

如果边权不大，那么可以二分答案，然后统计有多少条路径的长度不超过$mid$。

在二分答案之前对树进行点分治，在每个分治过程中将所有点到重心的距离从小到大排序，那么每次二分时只需要双指针统计方案数。

现在边权很大，可以用可持久线段树来维护高精度数，做到$O(\log n)$比较两个高精度数的大小，时间复杂度$O(n\log^3n)$。

最后一个问题是如何对高精度数进行二分。注意到答案只能是$a_i+a_j(1\leq i\leq j\leq cnt)$的形式，其中$a$是所有分治过程中点到重心的距离的集合的并。假设我们知道$l<ans<r$，那么我们可以通过双指针求出每个$a_i$和哪个范围的$a_j$相加在$(l,r)$之间，并统计处出这样的方案数$tot$。

• 如果$tot$不大，那么可以将它们全部暴力提取出来，在排序后的数组里二分，从而最小化二分轮数。
• 否则$tot$比较大，我们可以随机取一对这样的$(i,j)$，这不会导致期望二分轮数变大很多。

#include<cstdio>
#include<algorithm>
using namespace std;
typedef unsigned int U;
typedef long long ll;
typedef unsigned long long ull;
const int N=25010,CNT=500005,M=CNT*17,P=1000000007,LIM=150000;
int n,_,i,j,k,x,y,z;ll K;
int root[N],g[N],v[N<<1],w[N<<1],nxt[N<<1],ok[N<<1],ed,son[N],f[N],now,all;
int pool[CNT],cp,q[CNT<<1],cq,cnt,st[N<<1],en[N<<1],base[N<<1];
int pl[CNT],pr[CNT];
int tot,l[M],r[M],sum[M],val[M],p[N];ll sw[M],weight[N];
int LA,LB,RA,RB,MA,MB,ANSA,ANSB;
ll total;
U SX=335634763,SY=873658265,SZ=192849106,SW=746126501;
int ce;
struct E{int l,r;E(){}E(int _l,int _r){l=_l,r=_r;}}e[LIM+5];
inline ull xorshift128(){
  U t=SX^(SX<<11);
  SX=SY;
  SY=SZ;
  SZ=SW;
  return SW=SW^(SW>>19)^t^(t>>8);
}
inline ull myrand(){return (xorshift128()<<32)^xorshift128();}
int ins(int x,int a,int b,int c){
  int y=++tot;
  val[y]=val[x]+1;
  sum[y]=(sum[x]+p[c])%P;
  sw[y]=sw[x]+weight[c];
  if(a==b)return y;
  int mid=(a+b)>>1;
  if(c<=mid)l[y]=ins(l[x],a,mid,c),r[y]=r[x];
  else l[y]=l[x],r[y]=ins(r[x],mid+1,b,c);
  return y;
}
inline int compare(int A,int B,int C,int D){
  if(sw[A]+sw[B]==sw[C]+sw[D])return 0;
  int a=1,b=n,mid;
  while(a<b){
    mid=(a+b)>>1;
    if(sw[r[A]]+sw[r[B]]==sw[r[C]]+sw[r[D]]){
      b=mid;
      A=l[A];
      B=l[B];
      C=l[C];
      D=l[D];
    }else{
      a=mid+1;
      A=r[A];
      B=r[B];
      C=r[C];
      D=r[D];
    }
  }
  return val[A]+val[B]<val[C]+val[D]?-1:1;
}
inline bool cmp(int x,int y){return compare(x,0,y,0)<0;}
inline bool cmpe(const E&a,const E&b){return compare(a.l,a.r,b.l,b.r)<0;}
inline void add(int x,int y,int z){v[++ed]=y;w[ed]=z;nxt[ed]=g[x];g[x]=ed;ok[ed]=1;}
void findroot(int x,int y){
  son[x]=1;f[x]=0;
  for(int i=g[x];i;i=nxt[i])if(ok[i]&&v[i]!=y){
    findroot(v[i],x);
    son[x]+=son[v[i]];
    if(son[v[i]]>f[x])f[x]=son[v[i]];
  }
  if(all-son[x]>f[x])f[x]=all-son[x];
  if(f[x]<f[now])now=x;
}
void dfs1(int x,int y,int z){
  root[x]=z;
  pool[++cp]=z;
  for(int i=g[x];i;i=nxt[i])if(v[i]!=y&&ok[i])dfs1(v[i],x,ins(z,1,n,w[i]));
}
void dfs2(int x,int y){
  q[++cq]=root[x];
  for(int i=g[x];i;i=nxt[i])if(v[i]!=y&&ok[i])dfs2(v[i],x);
}
void solve(int x){
  int i;
  dfs1(x,0,0);
  base[++cnt]=1;
  st[cnt]=cq+1;
  dfs2(x,0);
  en[cnt]=cq;
  if(en[cnt]==st[cnt])cnt--,cq--;
  for(i=g[x];i;i=nxt[i])if(ok[i]){
    base[++cnt]=-1;
    st[cnt]=cq+1;
    dfs2(v[i],x);
    en[cnt]=cq;
    if(en[cnt]==st[cnt])cnt--,cq--;
  }
  for(i=g[x];i;i=nxt[i])if(ok[i]){
    ok[i^1]=0;
    f[0]=all=son[v[i]];
    findroot(v[i],now=0);
    solve(now);
  }
}
inline void dec(int l,int r){
  int i,j;
  for(i=l,j=r;i<=r;i++){
    while(j>i&&compare(MA,MB,q[i],q[j])<0)j--;
    if(j<=i)break;
    total-=j-i;
  }
}
inline void inc(int l,int r){
  int i,j;
  if(total>=K)return;
  for(i=l,j=r;i<=r;i++){
    while(j>i&&compare(MA,MB,q[i],q[j])<0)j--;
    if(j<=i)break;
    total+=j-i;
    if(total>=K)return;
  }
}
int main(){
  scanf("%d%lld",&n,&K);
  for(i=1;i<=n;i++)weight[i]=myrand();
  for(p[0]=i=1;i<=n;i++)p[i]=1LL*p[i-1]*n%P;
  for(ed=i=1;i<n;i++)scanf("%d%d%d",&x,&y,&z),add(x,y,z),add(y,x,z);
  f[0]=all=n;findroot(1,now=0);solve(now);
  sort(pool+1,pool+cp+1,cmp);
  for(i=1;i<=cp;i++)if(i==1||cmp(pool[i-1],pool[i]))pool[++_]=pool[i];
  cp=_;
  for(i=1;i<=cnt;i++)sort(q+st[i],q+en[i]+1,cmp);
  LA=LB=pool[1];
  RA=RB=ANSA=ANSB=pool[cp];
  while(1){
    ll have=0;
    for(i=1,j=cp+1,k=cp;i<=cp;i++){
      while(j-1>i&&compare(LA,LB,pool[i],pool[j-1])<0)j--;
      while(k>i&&compare(RA,RB,pool[i],pool[k])<=0)k--;
      j=max(j,i+1);
      pl[i]=j,pr[i]=k;
      if(j>i&&j<=k)have+=k-j+1;
    }
    if(have<=LIM){
      for(i=1;i<=cp;i++){
        j=pl[i],k=pr[i];
        if(j>i&&j<=k)for(x=j;x<=k;x++)e[++ce]=E(pool[i],pool[x]);
      }
      break;
    }
    have=myrand()%have+1;
    for(i=1;i<=cp;i++){
      j=pl[i],k=pr[i];
      if(j>i&&j<=k){
        if(k-j+1>=have){
          MA=pool[i];
          MB=pool[pl[i]+have-1];
          break;
        }
        have-=k-j+1;
      }
    }
    total=0;
    for(i=1;i<=cnt;i++)if(base[i]==-1)dec(st[i],en[i]);
    for(i=1;i<=cnt;i++)if(base[i]==1)inc(st[i],en[i]);
    if(total>=K){
      ANSA=MA;
      ANSB=MB;
      RA=MA;
      RB=MB;
    }else{
      LA=MA;
      LB=MB;
    }
  }
  if(ce>1)sort(e+1,e+ce+1,cmpe);
  int l=1,r=ce;
  while(l<=r){
    int mid=(l+r)>>1;
    MA=e[mid].l;
    MB=e[mid].r;
    total=0;
    for(i=1;i<=cnt;i++)if(base[i]==-1)dec(st[i],en[i]);
    for(i=1;i<=cnt;i++)if(base[i]==1)inc(st[i],en[i]);
    if(total>=K){
      ANSA=MA;
      ANSB=MB;
      r=mid-1;
    }else{
      l=mid+1;
    }
  }
  printf("%d",(sum[ANSA]+sum[ANSB])%P);
}