【动态规划DP】传娃娃-C++

传娃娃
描述
学习空闲之余，小信经常带着同学们做游戏，最近小信发明了一个好玩的新游戏：n 位同学围成一个圈，同学 A 手里拿着一个布娃娃。小信喊游戏开始，每位手里拿着娃娃的同学可以选择将娃娃传给左边或者右边的同学，当小信喊游戏结束时，停止传娃娃。此时手里拿着娃娃的同学即是败者。
玩了几轮之后，小信想到一个问题：有多少种不同的方法，使得从同学 A 开始传娃娃，传了 m 次之后又回到了同学 A 手里。两种方法，如果接娃娃的同学不同，或者接娃娃的顺序不同均视为不同的方法。例如 1->2->3->1和 1->3->2->1 是两种不同的方法。
输入
输入一行，输入两个整数 n,m(3≤n≤30,1≤m≤30)，表示一共有 n 位同学一起游戏，一共传 m 次娃娃。
输出
输出一行，输出一个整数，表示一共有多少种不同的传娃娃方法。
输入样例 1 
3 3
输出样例 1
2

这道题初一看好像真的想不出该怎么做，但是在同机房大佬的提醒下 应该用DP！

然后就想状态转移方程。。这就炸了。实在想不出该咋玩。于是我试着去画图。（别嫌弃摸鱼酱的图丑）

就以n=6时为例。

初始状态：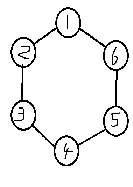

我们用dp[m][n]表示第m次传递后第n个小朋友的传娃娃方法数，很明显，我们需要求的即是dp[m][1]的值。找到边界值：dp[0][1]=1;然后可以发现，一个状态转移方程是无法解决这个比较复杂的dp的，需要添加if语句达到效果。

于是我开始讨论有哪些可能。因为这道题是直接用的dp，并没有构建环，所以这是需要特殊考虑的。然后，我们发现，第i次传递后的点k的方案数，只能由第i-1次传递后的点k的左右两人的方案数之和来得到！原理如下图！



但是如上所述，当这个点是1或n时需要特判，所以情况分为三种：

①这个点是1时：dp[i][j]=dp[i-1][j+1]+dp[i-1][n];

②这个点是n时：dp[i][j]=dp[i-1][j-1]+dp[i-1][1];

③这个点是普通点（非1非n时）:dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1];

然后双重循环，外层1…->m,内层1…->n,完事输出dp[m][1]即可。

AC代码如下：

#include<bits/stdc++.h>
using namespace std;
int dp[31][31];
int main()
{
	int n,m;
	cin>>n>>m;
	dp[0][1]=1;
	for (int i=1;i<=m;i++)
	{
		for (int j=1;j<=n;j++)
		{
			if (j==n)
			{
				dp[i][j]=dp[i-1][j-1]+dp[i-1][1];
			}
			else if(j==1)
				{
					dp[i][j]=dp[i-1][j+1]+dp[i-1][n];
				}
			else
			{
				dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1];
			}
		}
	}
	cout<<dp[m][1]<<endl;
	return 0;
}

ov.