CCPC 2019 秦皇岛 Angle Beats

题目

给出P个点，然后给出Q个询问，问从P中选出两个点和给的点能组成直角三角形的方法个数。-O2，时间限制5秒。

\[2\leqslant P\leqslant 2000,\qquad 1\leqslant Q\leqslant2000\]

\[\left\lvert x_i\right\rvert \leqslant 10^9,\left\lvert y_i\right\rvert \leqslant 10^9\]

题解

卡常数的题目……刚开始想了个$n^2\times q$的做法= =显然过不了

稍微思考就分别以P个点和Q个点为中心对P个点进行极角排序，然后分两种情况（注意Q的位置）

1、

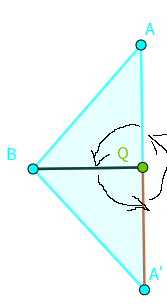
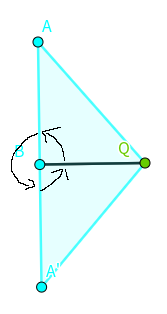
2、

对于1，可以枚举每一条与Q相连的边，然后顺时针寻找和这条边垂直的，类似于旋转卡壳，两个垂直的边会同时旋转，虽然极角排序需要$\mathcal{O}(n\log n)$的时间，二分和这个比起来在渐进意义上没有改变，但是因为要卡常，所以能减少一点是一点= =

对于2，可以预处理出以P个点为中心的极角排序，然后看和Q相连的边，找直角……（可以思考下如果找到A怎么办233（反正也不会重复，找到了也没事））

那么1可以$q\times n\log n+q\times n$

2可以$q\times q \log n$

因为要卡常，还需要很多技巧。

需要充分利用CPU的缓存，经常用的数据要放在一起，如果B要A的数据，C要B的数据，AAABBBCCC地做会比ABCABCABC慢，寄存快于缓存，缓存快于内存= =虽然用什么都是系统和编译器决定的，但是只有尽量放一起才能命中缓存。

对于2，$AB$和$BA'$两个垂直其实只用考虑斜率，那么在排序的时候就不用管象限了。

极角排序还是可以用斜率的，排序起来比叉乘快得多……而且比较大小也不必要非要按照分数的大小关系，只要保持有序就可以二分统计数字，这样就可以化为最简以后直接排序。

除了排序还可以将斜率进行HASH，unordered_map就可以用

（其实上面两种技巧我一个都不会= =看别人的代码卡过的）

AC代码：

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cctype>
using namespace std;
#define REP(i,a,b) for(register int i=(a);i<(b);i++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...) (void)0
#endif // LOCAL
#define D Point
#define CD const D
struct Point {
	long long x,y;
	int k;
};
inline bool operator<(CD&l, CD&r) {
	return l.x<r.x || (l.x==r.x && l.y<r.y);
}
inline D operator-(D a, D b) {
	return (D){a.x-b.x, a.y-b.y};
}
#define dot(a, b) (a.x*b.x+a.y*b.y)
#define cross(a,b) (a.x*b.y-a.y*b.x)
inline int qquad(D a) {
	if(a.x>0 && a.y>=0) return 1;
	if(a.x<=0 && a.y>0) return 2;
	if(a.x<0 && a.y<=0) return 3;
	return 4;
}
inline bool cmp(D l, D r) {
	if(l.k==r.k) {return cross(l,r)>0LL;}
	return l.k<r.k;
}
const int T[]={0,3,4,1,2};
const int TT[]={0,2,3,4,1};
inline D rotCCW(D p) {return (D){-p.y,p.x,TT[p.k]};}
#undef D
#undef CD
#define LL long long
template<class T>
inline void read(T&x) {
	x=0; int f=1; char ch=getchar();
	while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();}
	while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();}
	x*=f;
}
inline LL gcd(LL a, LL b) {
	return b==0?a:gcd(b,a%b);
}
Point P[2007],A[2007];
Point Z[2007];
Point zi[2007*2];
inline int findge(Point *t, int l, int r, Point k) {
	while(l<r) {
		int m=l+r>>1;
		if(t[m]<k) l=m+1;
		else r=m;
	}
	return l;
}
inline int findg(Point *t, int l, int r, Point k) {
	while(l<r) {
		int m=l+r>>1;
		if(k<t[m]) r=m;
		else l=m+1;
	}
	return l;
}
int aaa[2007];
int main() {
	int n,q; read(n); read(q);
	REP(i,0,n) {
		read(P[i].x); read(P[i].y);
	}
	REP(i,0,q) {
		read(A[i].x); read(A[i].y);
	}
	REP(i,0,q){
		REP(j,0,n) {
			zi[j]=P[j]-A[i];
			zi[j].k=qquad(zi[j]);
		}
		sort(zi,zi+n,cmp);
		REP(j,0,n) zi[j+n]=zi[j];
		for(register int j=0,k=0,l=0,m=0; j<n;) {
			for(; k<j+n && cross(zi[j],zi[k])==0 && dot(zi[j],zi[k])>0; k++);
			for(l=max(k,m); l<j+n && cross(zi[j],zi[l])>0 && dot(zi[j],zi[l])>0; l++);
			for(m=max(m,l); m<j+n && cross(zi[j],zi[m])>0 && dot(zi[j],zi[m])==0; m++);
			aaa[i]+=(k-j)*(m-l);
			j=k;
		}
	}
	REP(j,0,n) {
		int p=0;
	   	REP(k,0,n) if(k!=j) {
			Z[p]=P[k]-P[j];
			Z[p].k=qquad(Z[p]);
			LL g=gcd(Z[p].x,Z[p].y);
			Z[p].x/=g, Z[p].y/=g;
			if(Z[p].x<0) Z[p].x*=-1, Z[p].y*=-1;
			p++;
		}
		sort(Z,Z+p);

		REP(i,0,q) {
			Point z;
			Point *L, *R;
			z=P[j]-A[i];
			int t=-z.y;
			z.y=z.x; z.x=t;

			LL g=gcd(z.x,z.y);
			z.x/=g, z.y/=g;
			if(z.x<0) z.x=-z.x, z.y=-z.y;

			aaa[i]+=findg(Z,0,n-1,z)-findge(Z,0,n-1,z);
		} //DBG("~~~%d\n", aaa[i]);
	}
	REP(i,0,q) printf("%d\n", aaa[i]);

	return 0;
}

对了就能拿银（快哭了）