换根DP（二次扫描）

参考来自这里：

https://blog.csdn.net/qq_41286356/article/details/94554729

题目在这里

https://ac.nowcoder.com/acm/contest/375/C

这题真的好，算是排列组合+树形DP的结合 吧

这题换个问法就是 ：   给树节点标号，使得所有节点的父节点都比子节点大，这样的编号方法有几种？

第一次扫描，计算一个根：

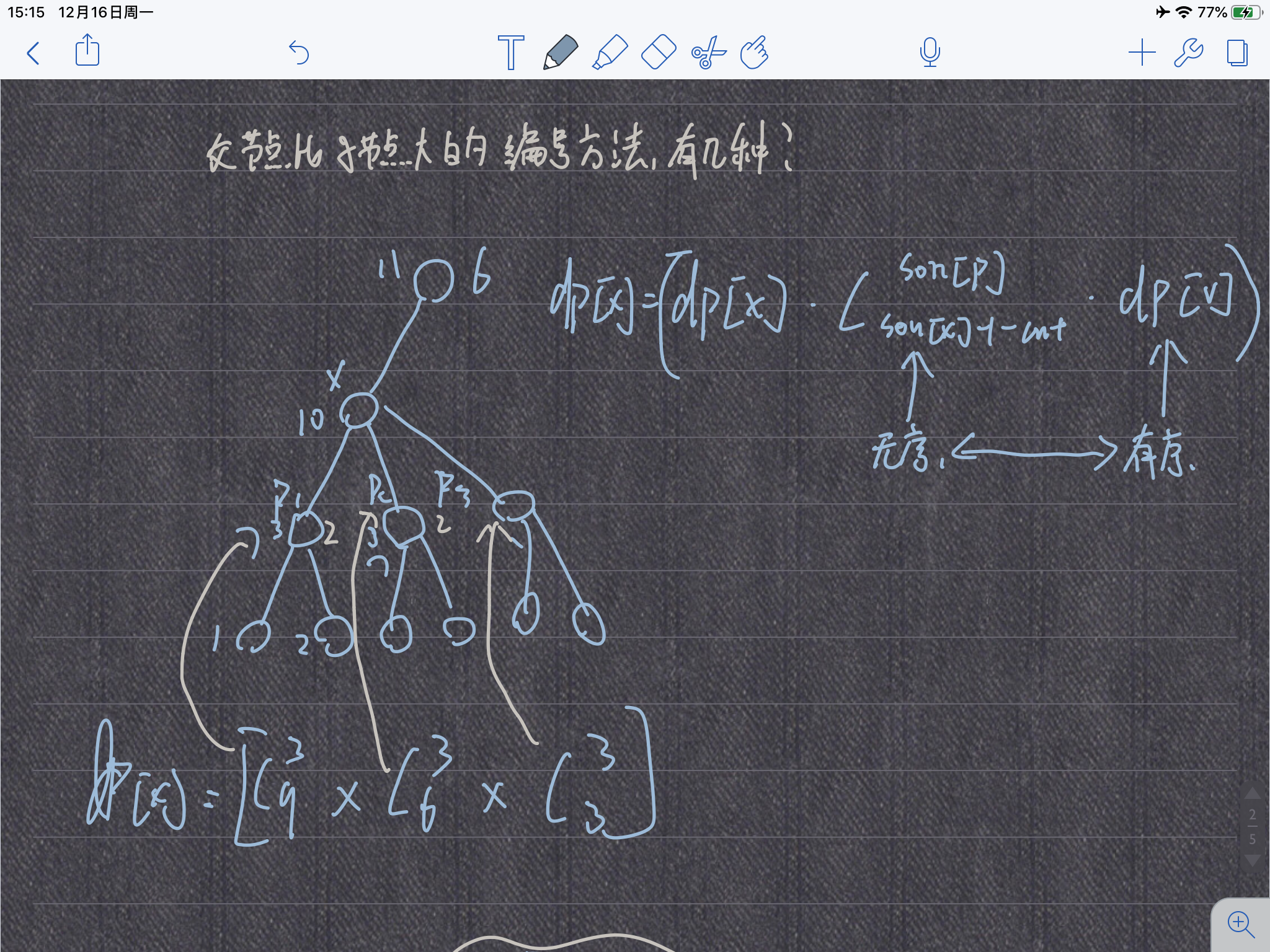
第二次扫描，推进算出所有根

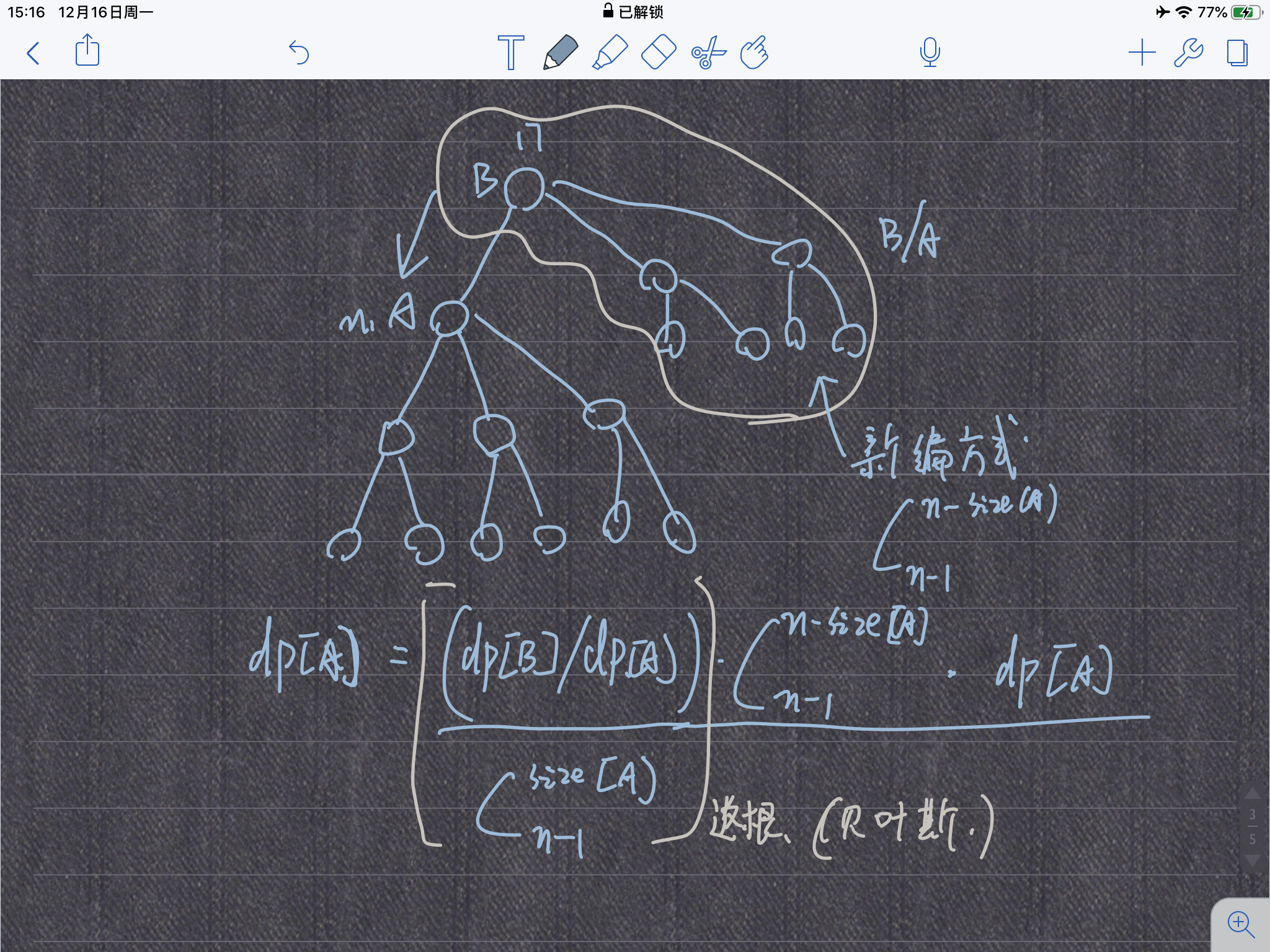
妙啊！

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cstdio>
#define maxn 100010
using namespace std;
typedef long long ll;
const ll mod = 998244353;
vector<int>G[maxn];
void insert(int be, int en) {
	G[be].push_back(en);
}

ll inv(ll a) {
	ll n = mod - 2;
	ll res = 1;
	while (n) {
		if (n & 1) {
			res = (res*a) % mod;
		}
		n >>= 1;
		a = (a*a) % mod;
	}
	return res;
}

ll dp[maxn];
ll in[maxn];
ll C(int n, int m) {
	ll ans = (in[n] * inv(in[m])) % mod;
	ans = (ans * inv(in[n - m])) % mod;
	return ans;
}

ll son[maxn];
int n;

int dfs(int x,int fa) {
	dp[x] = son[x] = 1;

	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i];
		if (p == fa) continue;
		dfs(p, x);
		son[x] += son[p];
	}
	ll cnt = 0;
	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i];
		if (p == fa) continue;
		ll a = son[x] - 1 - cnt;
		ll b = son[p];
		dp[x] = (((dp[x] * C(a, b)) % mod)*dp[p]) % mod;
		cnt += son[p];
	}
	return 0;
}

int dfs1(int x, int fa) {
	for(int i = 0; i < G[x].size(); i++) {
		int p = G[x][i];
		if (p == fa) continue;
		ll tmp = ((dp[x] * inv(dp[p])) % mod)*inv(C(n - 1, son[p])) % mod;
		dp[p] = (((dp[p] * C(n - 1, n - son[p])) % mod)*tmp )% mod;
		dfs1(p, x);
	}
	return 0;
}

int main() {

	int be, en;
	in[0] = 1;
	for (int i = 1; i <= 1e5+4; i++) {
		in[i] = (in[i - 1] * i) % mod;
	}

	scanf("%d", &n);

	for (int i = 1; i < n; i++) {
		scanf("%d%d", &be, &en);
		insert(be, en);
		insert(en, be);
	}
	dfs(1, -1);
	dfs1(1, -1);
	ll ans = 0;
	for (int i = 1; i <= n; i++) {
		ans = (ans + dp[i]) % mod;
	}
	printf("%lld\n", ans);
	return 0;
}