Leetcode958. Check Completeness of a Binary Tree二叉树的完全验证性

给定一个二叉树，确定它是否是一个完全二叉树。

百度百科中对完全二叉树的定义如下：

若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（注：第 h 层可能包含 1~ 2h 个节点。）

示例 1：

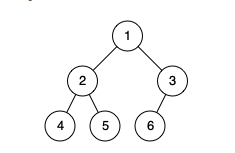
输入：[1,2,3,4,5,6] 输出：true 解释：最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。

示例 2：

输入：[1,2,3,4,5,null,7] 输出：false 解释：值为 7 的结点没有尽可能靠向左侧。

提示：

1. 树中将会有 1 到 100 个结点。

个人递归方法：

class Solution {
	 bool isTheEnd = false;
	 int depth = 0;
 public:
	 bool isCompleteTree(TreeNode* root)
	 {
		 if (root == NULL)
			 return true;
		 depth = GetDepth(root);
		 return GetAns(root, 1);
	 }

	 int GetDepth(TreeNode *root)
	 {
		 if (root == NULL)
			 return 0;
		 return max(GetDepth(root->left), GetDepth(root->right)) + 1;
	 }

	 bool GetAns(TreeNode *root, int dep)
	 {
//只有根节点的情况，不用判空，因为不会递归到那
		 if (dep == depth)
		 {
			 return true;
		 }
		 if (dep < depth - 1)
		 {
			 if (root->left == NULL || root->right == NULL)
				 return false;
			 return GetAns(root->left, dep + 1) && GetAns(root->right, dep + 1);
		 }
		 else if (dep == depth - 1)
		 {
			 if (isTheEnd)
			 {
				 if (root->left != NULL || root->right != NULL)
					 return false;
				 return true;
			 }
			 else
			 {
				 if (root->left == NULL)
				 {
					 if (root->right != NULL)
						 return false;
					 isTheEnd = true;
					 return true;
				 }
				 if (root->right == NULL)
				 {
					 isTheEnd = true;
					 return true;
				 }
				 return true;
			 }
		 }
	 }
 };

广度优先遍历法（推荐）：

bool isCompleteTree(TreeNode* root) {
        queue<TreeNode *> que;
        que.push(root);
        while(!que.empty())
        {
            TreeNode * node = que.front();
            que.pop();
            if(!node)
            {
                break;
            }
            else
            {
                que.push(node->left);
                que.push(node->right);
            }
        }
        while(!que.empty())
        {
            TreeNode * node=que.front();
            if(node)
                return false;
            que.pop();
        }
        return true;
    }