hdu - 4990

Read the program below carefully then answer the question.
    #pragma comment(linker, "/STACK:1024000000,1024000000")
    #include <cstdio>
    #include<iostream>
    #include <cstring>
    #include <cmath>
    #include <algorithm>
    #include<vector>

const int MAX=100000*2;
    const int INF=1e9;

int main()
    {
      int n,m,ans,i;
      while(scanf("%d%d",&n,&m)!=EOF)
      {
        ans=0;
        for(i=1;i<=n;i++)
        {
          if(i&1)ans=(ans*2+1)%m;
          else ans=ans*2%m;
        }
        printf("%d\n",ans);
      }
      return 0;
    }
Input
    Multi test cases，each line will contain two integers n and m. Process to end of file.
    [Technical Specification]
    1<=n, m <= 1000000000
Output
    For each case，output an integer，represents the output of above program.
Sample Input

1 10
    3 100

Sample Output

1
    5

题意 ： 优化按照已给的程序

思路 ： 用已有的程序跑出前几个答案，找规律， fn = f n-1 + 2 * f n-2 + 1 , 重点还是构造矩阵，带常数项如何构造出矩阵

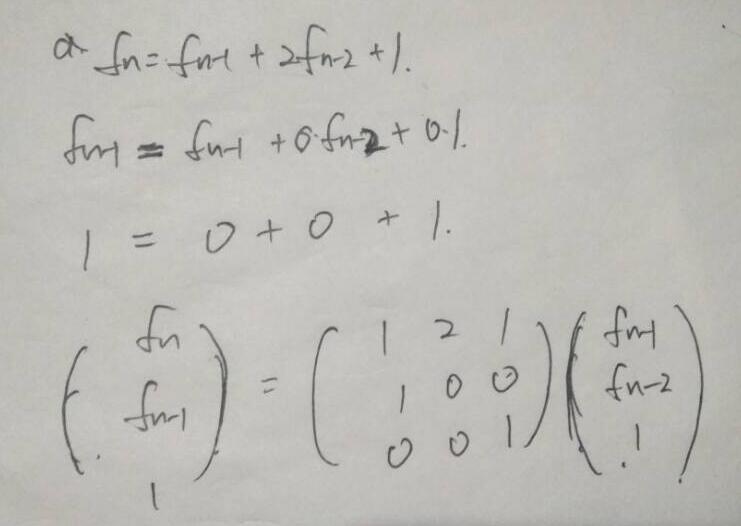
代码示例 ：

struct mat
{
    ll a[3][3];
};

ll m;

mat mul(mat a, mat b){
    mat r;
    memset(r.a, 0, sizeof(r.a));

    for(int i = 0; i < 3; i++){
        for(int k = 0; k < 3; k++){
            if (a.a[i][k]){
                for(int j = 0; j < 3; j++){
                    if (b.a[k][j]){
                        r.a[i][j] += (a.a[i][k]*b.a[k][j])%m;
                        r.a[i][j] %= m;
                    }
                }
            }
        }
    }
    return r;
}

mat pow(mat a, ll n){
    mat b;
    memset(b.a, 0, sizeof(b.a));
    b.a[0][0] = b.a[1][1] = b.a[2][2] = 1;

    while(n){
        if (n&1) b = mul(a, b); //
        a = mul(a, a);
        n >>= 1;
    }
    return b;
}

int main() {
    ll n;

    while(~scanf("%lld%lld", &n, &m)){
        mat a;
        memset(a.a, 0, sizeof(a.a));
        a.a[0][0] = a.a[1][0] = a.a[0][2] = a.a[2][2] = 1;
        a.a[0][1] = 2;
        if (n == 1) {
            printf("%lld\n", 1%m);
        }
        else if (n == 2){
            printf("%lld\n", 2%m);
        }
        else {
            a = pow(a, n-2);
            printf("%lld\n", (a.a[0][0]*2%m+a.a[0][1]%m+a.a[0][2]%m)%m);
        }

    }

    return 0;
}