逻辑回归代码demo

程序所用文件：https://files.cnblogs.com/files/henuliulei/%E5%9B%9E%E5%BD%92%E5%88%86%E7%B1%BB%E6%95%B0%E6%8D%AE.zip

概念

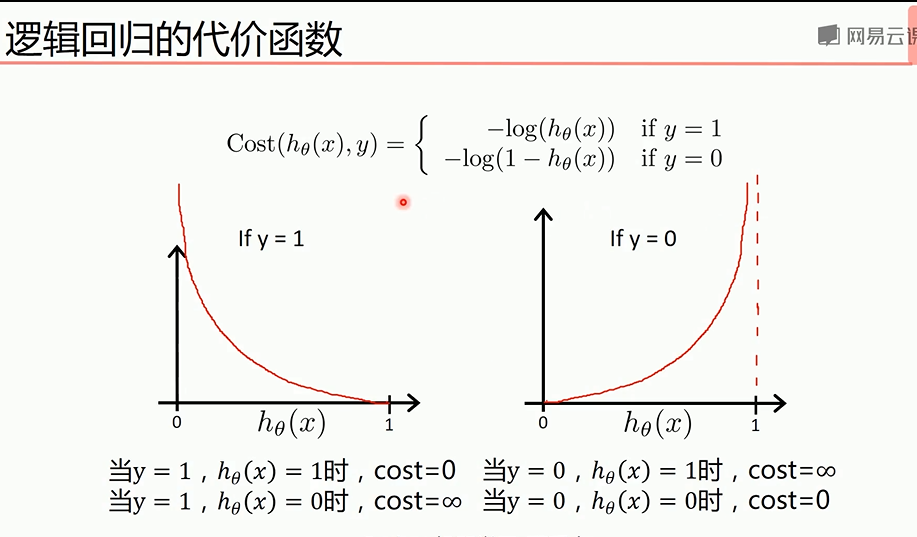
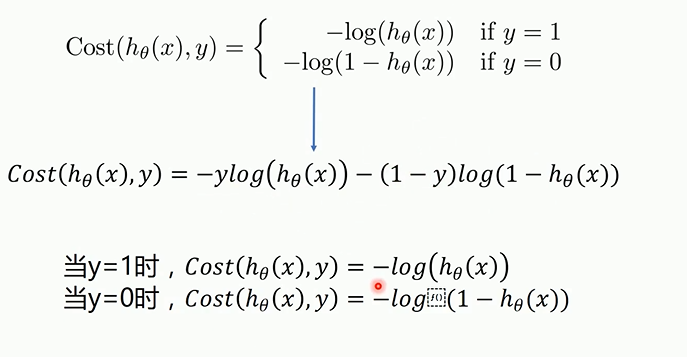
代价函数关于参数的偏导

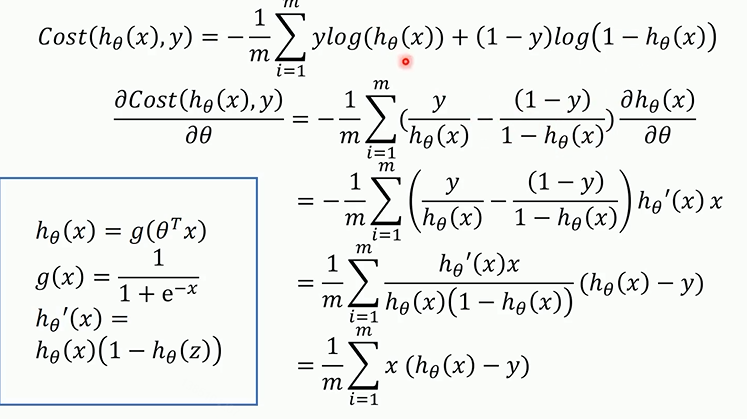
梯度下降法最终的推导公式如下

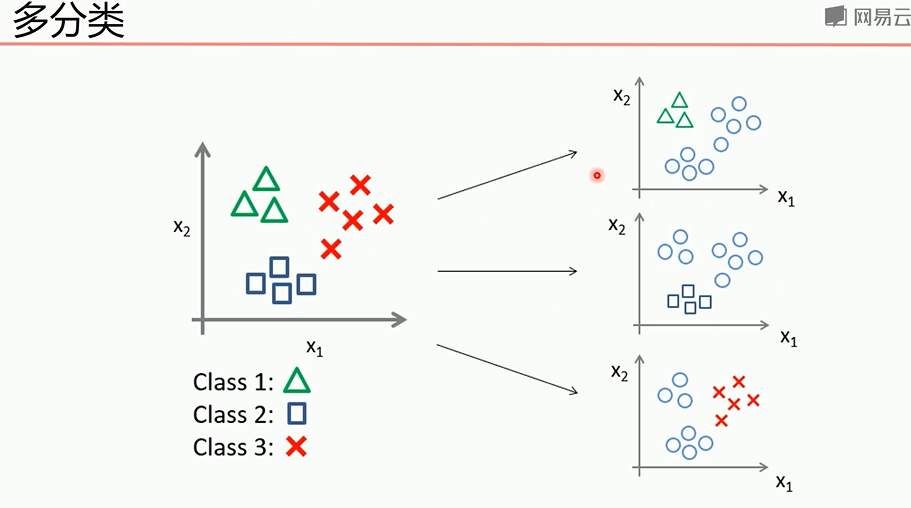
多分类问题可以转为2分类问题

正则化处理可以防止过拟合，下面是正则化后的代价函数和求导后的式子

正确率和召回率F1指标

我们希望自己预测的结果希望更准确那么查准率就更高，如果希望更获得更多数量的正确结果，那么查全率更重要，综合考虑可以用F1指标

关于正则化为啥可以防止过拟合的理解

梯度下降法实现线性逻辑回归

 import matplotlib.pyplot as plt

 import numpy as np

 from sklearn.metrics import classification_report#分类

 from sklearn import preprocessing#预测

 # 数据是否需要标准化

 scale = True#True是需要，False是不需要，标准化后效果更好，标准化之前可以画图看出可视化结果

 scale = False

 # 载入数据

 data = np.genfromtxt("LR-testSet.csv", delimiter=",")

 x_data = data[:, :-]

 y_data = data[:, -]

 def plot():

     x0 = []

     x1 = []

     y0 = []

     y1 = []

     # 切分不同类别的数据

     for i in range(len(x_data)):

         if y_data[i] == :

             x0.append(x_data[i, ])

             y0.append(x_data[i, ])

         else:

             x1.append(x_data[i, ])

             y1.append(x_data[i, ])

     # 画图

     scatter0 = plt.scatter(x0, y0, c='b', marker='o')

     scatter1 = plt.scatter(x1, y1, c='r', marker='x')

     # 画图例

     plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')

 plot()

 plt.show()

 # 数据处理，添加偏置项

 x_data = data[:,:-]

 y_data = data[:,-,np.newaxis]

 print(np.mat(x_data).shape)

 print(np.mat(y_data).shape)

 # 给样本添加偏置项

 X_data = np.concatenate((np.ones((,)),x_data),axis=)

 print(X_data.shape)

 def sigmoid(x):

     return 1.0 / ( + np.exp(-x))

 def cost(xMat, yMat, ws):

     left = np.multiply(yMat, np.log(sigmoid(xMat * ws)))

     right = np.multiply( - yMat, np.log( - sigmoid(xMat * ws)))

     return np.sum(left + right) / -(len(xMat))

 def gradAscent(xArr, yArr):

     if scale == True:

         xArr = preprocessing.scale(xArr)

     xMat = np.mat(xArr)

     yMat = np.mat(yArr)

     lr = 0.001

     epochs =

     costList = []

     # 计算数据行列数

     # 行代表数据个数，列代表权值个数

     m, n = np.shape(xMat)

     # 初始化权值

     ws = np.mat(np.ones((n, )))

     for i in range(epochs + ):

         # xMat和weights矩阵相乘

         h = sigmoid(xMat * ws)

         # 计算误差

         ws_grad = xMat.T * (h - yMat) / m

         ws = ws - lr * ws_grad

         if i %  == :

             costList.append(cost(xMat, yMat, ws))

     return ws, costList

 # 训练模型，得到权值和cost值的变化

 ws,costList = gradAscent(X_data, y_data)

 print(ws)

 if scale == False:

     # 画图决策边界

     plot()

     x_test = [[-],[]]

     y_test = (-ws[] - x_test*ws[])/ws[]

     plt.plot(x_test, y_test, 'k')

     plt.show()

 # 画图 loss值的变化

 x = np.linspace(, , )

 plt.plot(x, costList, c='r')

 plt.title('Train')

 plt.xlabel('Epochs')

 plt.ylabel('Cost')

 plt.show()

 # 预测

 def predict(x_data, ws):

     if scale == True:

         x_data = preprocessing.scale(x_data)

     xMat = np.mat(x_data)

     ws = np.mat(ws)

     return [ if x >= 0.5 else  for x in sigmoid(xMat*ws)]

 predictions = predict(X_data, ws)

 print(classification_report(y_data, predictions))#计算预测的分

sklearn实现线性逻辑回归

 import matplotlib.pyplot as plt

 import numpy as np

 from sklearn.metrics import classification_report

 from sklearn import preprocessing

 from sklearn import linear_model

 # 数据是否需要标准化

 scale = False

 # 载入数据

 data = np.genfromtxt("LR-testSet.csv", delimiter=",")

 x_data = data[:, :-]

 y_data = data[:, -]

 def plot():

     x0 = []

     x1 = []

     y0 = []

     y1 = []

     # 切分不同类别的数据

     for i in range(len(x_data)):

         if y_data[i] == :

             x0.append(x_data[i, ])

             y0.append(x_data[i, ])

         else:

             x1.append(x_data[i, ])

             y1.append(x_data[i, ])

     # 画图

     scatter0 = plt.scatter(x0, y0, c='b', marker='o')

     scatter1 = plt.scatter(x1, y1, c='r', marker='x')

     # 画图例

     plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')

 plot()

 plt.show()

 logistic = linear_model.LogisticRegression()

 logistic.fit(x_data, y_data)

 if scale == False:

     # 画图决策边界

     plot()

     x_test = np.array([[-],[]])

     y_test = (-logistic.intercept_ - x_test*logistic.coef_[][])/logistic.coef_[][]

     plt.plot(x_test, y_test, 'k')

     plt.show()

 predictions = logistic.predict(x_data)

 print(classification_report(y_data, predictions))

梯度下降法实现非线性逻辑回归

 import matplotlib.pyplot as plt

 import numpy as np

 from sklearn.metrics import classification_report

 from sklearn import preprocessing

 from sklearn.preprocessing import PolynomialFeatures

 # 数据是否需要标准化

 scale = False

 # 载入数据

 data = np.genfromtxt("LR-testSet2.txt", delimiter=",")

 x_data = data[:, :-]

 y_data = data[:, -, np.newaxis]

 def plot():

     x0 = []

     x1 = []

     y0 = []

     y1 = []

     # 切分不同类别的数据

     for i in range(len(x_data)):

         if y_data[i] == :

             x0.append(x_data[i, ])

             y0.append(x_data[i, ])

         else:

             x1.append(x_data[i, ])

             y1.append(x_data[i, ])

     # 画图

     scatter0 = plt.scatter(x0, y0, c='b', marker='o')

     scatter1 = plt.scatter(x1, y1, c='r', marker='x')

     # 画图例

     plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')

 plot()

 plt.show()

 # 定义多项式回归,degree的值可以调节多项式的特征

 poly_reg  = PolynomialFeatures(degree=)

 # 特征处理

 x_poly = poly_reg.fit_transform(x_data)

 def sigmoid(x):

     return 1.0 / ( + np.exp(-x))

 def cost(xMat, yMat, ws):

     left = np.multiply(yMat, np.log(sigmoid(xMat * ws)))

     right = np.multiply( - yMat, np.log( - sigmoid(xMat * ws)))

     return np.sum(left + right) / -(len(xMat))

 def gradAscent(xArr, yArr):

     if scale == True:

         xArr = preprocessing.scale(xArr)

     xMat = np.mat(xArr)

     yMat = np.mat(yArr)

     lr = 0.03

     epochs =

     costList = []

     # 计算数据列数，有几列就有几个权值

     m, n = np.shape(xMat)

     # 初始化权值

     ws = np.mat(np.ones((n, )))

     for i in range(epochs + ):

         # xMat和weights矩阵相乘

         h = sigmoid(xMat * ws)

         # 计算误差

         ws_grad = xMat.T * (h - yMat) / m

         ws = ws - lr * ws_grad

         if i %  == :

             costList.append(cost(xMat, yMat, ws))

     return ws, costList

 # 训练模型，得到权值和cost值的变化

 ws,costList = gradAscent(x_poly, y_data)

 print(ws)

 # 获取数据值所在的范围

 x_min, x_max = x_data[:, ].min() - , x_data[:, ].max() +

 y_min, y_max = x_data[:, ].min() - , x_data[:, ].max() + 

 # 生成网格矩阵

 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),

                      np.arange(y_min, y_max, 0.02))

 #print(xx.shape)#xx和yy有相同shape，xx的每行相同，总行数取决于yy的范围

 #print(yy.shape)#xx和yy有相同shape，yy的每列相同，总行数取决于xx的范围

 # np.r_按row来组合array，

 # np.c_按colunm来组合array

 # >>> a = np.array([,,])

 # >>> b = np.array([,,])

 # >>> np.r_[a,b]

 # array([, , , , , ])

 # >>> np.c_[a,b]

 # array([[, ],

 #        [, ],

 #        [, ]])

 # >>> np.c_[a,[,,],b]

 # array([[, , ],

 #        [, , ],

 #        [, , ]])

 z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]).dot(np.array(ws)))# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据

 for i in range(len(z)):

     if z[i] > 0.5:

         z[i] =

     else:

         z[i] =

 print(z)

 z = z.reshape(xx.shape)

 # 等高线图

 cs = plt.contourf(xx, yy, z)

 plot()

 plt.show()

 # 预测

 def predict(x_data, ws):

 #     if scale == True:

 #         x_data = preprocessing.scale(x_data)

     xMat = np.mat(x_data)

     ws = np.mat(ws)

     return [ if x >= 0.5 else  for x in sigmoid(xMat*ws)]

 predictions = predict(x_poly, ws)

 print(classification_report(y_data, predictions))

sklearn实现非线性逻辑回归

 import numpy as np

 import matplotlib.pyplot as plt

 from sklearn import linear_model

 from sklearn.datasets import make_gaussian_quantiles

 from sklearn.preprocessing import PolynomialFeatures

 # 生成2维正态分布，生成的数据按分位数分为两类，500个样本,2个样本特征

 # 可以生成两类或多类数据

 x_data, y_data = make_gaussian_quantiles(n_samples=, n_features=,n_classes=)#生成500个样本，2个特征，2个类别

 plt.scatter(x_data[:, ], x_data[:, ], c=y_data)

 plt.show()

 logistic = linear_model.LogisticRegression()

 logistic.fit(x_data, y_data)

 # 获取数据值所在的范围

 x_min, x_max = x_data[:, ].min() - , x_data[:, ].max() +

 y_min, y_max = x_data[:, ].min() - , x_data[:, ].max() +

 # 生成网格矩阵

 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),

                      np.arange(y_min, y_max, 0.02))

 z = logistic.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据

 z = z.reshape(xx.shape)

 # 等高线图

 cs = plt.contourf(xx, yy, z)

 # 样本散点图

 plt.scatter(x_data[:, ], x_data[:, ], c=y_data)

 plt.show()

 print('score:',logistic.score(x_data,y_data))#使用线性逻辑回归，得分很低

 # 定义多项式回归,degree的值可以调节多项式的特征

 poly_reg  = PolynomialFeatures(degree=)

 # 特征处理

 x_poly = poly_reg.fit_transform(x_data)

 # 定义逻辑回归模型

 logistic = linear_model.LogisticRegression()

 # 训练模型

 logistic.fit(x_poly, y_data)

 # 获取数据值所在的范围

 x_min, x_max = x_data[:, ].min() - , x_data[:, ].max() +

 y_min, y_max = x_data[:, ].min() - , x_data[:, ].max() + 

 # 生成网格矩阵

 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),

                      np.arange(y_min, y_max, 0.02))

 z = logistic.predict(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]))# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据

 z = z.reshape(xx.shape)

 # 等高线图

 cs = plt.contourf(xx, yy, z)

 # 样本散点图

 plt.scatter(x_data[:, ], x_data[:, ], c=y_data)

 plt.show()

 print('score:',logistic.score(x_poly,y_data))#得分很高

逻辑回归代码demo的更多相关文章

[DL] 基于theano.tensor.dot的逻辑回归代码中的SGD部分的疑问探幽
在Hinton的教程中, 使用Python的theano库搭建的CNN是其中重要一环, 而其中的所谓的SGD - stochastic gradient descend算法又是如何实现的呢? 看下面源 ...
逻辑回归原理（python代码实现）
Logistic Regression Classifier逻辑回归主要思想就是用最大似然概率方法构建出方程,为最大化方程,利用牛顿梯度上升求解方程参数. 优点:计算代价不高,易于理解和实现. 缺点: ...
Spark Mllib逻辑回归算法分析
原创文章,转载请注明: 转载自http://www.cnblogs.com/tovin/p/3816289.html 本文以spark 1.0.0版本MLlib算法为准进行分析一.代码结构逻辑回归 ...
【原】Coursera—Andrew Ng机器学习—编程作业 Programming Exercise 3—多分类逻辑回归和神经网络
作业说明 Exercise 3,Week 4,使用Octave实现图片中手写数字 0-9 的识别,采用两种方式(1)多分类逻辑回归(2)多分类神经网络.对比结果. (1)多分类逻辑回归:实现 lrCo ...
机器学习/逻辑回归（logistic regression）/--附python代码
个人分类: 机器学习本文为吴恩达<机器学习>课程的读书笔记,并用python实现. 前一篇讲了线性回归,这一篇讲逻辑回归,有了上一篇的基础,这一篇的内容会显得比较简单. 逻辑回归(log ...
逻辑回归(Logistic Regression)详解,公式推导及代码实现
逻辑回归(Logistic Regression) 什么是逻辑回归: 逻辑回归(Logistic Regression)是一种基于概率的模式识别算法,虽然名字中带"回归",但实际上 ...
python sklearn库实现逻辑回归的实例代码
Sklearn简介 Scikit-learn(sklearn)是机器学习中常用的第三方模块,对常用的机器学习方法进行了封装,包括回归(Regression).降维(Dimensionality Red ...
Iris花逻辑回归与实现
Iris花的分类是经典的逻辑回归的代表:但是其代码中包含了大量的python库的核心处理模式,这篇文章就是剖析python代码的文章. #取用下标为2,3的两个feture,分别是花的宽度和长度: # ...
用R做逻辑回归之汽车贷款违约模型
数据说明本数据是一份汽车贷款违约数据 application_id 申请者ID account_number 账户号 bad_ind 是否违约 vehicle_year ...

随机推荐

Linux ls 命令实现（简化版）
在学习linux系统编程的时候,实现了ls命令的简化版本号. 实现的功能例如以下: 1. 每种文件类型有自己的颜色 (- 普通文件, d 文件夹文件, l 链接文件. c 字符设备文件. b 快设备文 ...
取地址栏query
GetQueryParm () { var name, value var str = window.location.href var num = str.indexOf(' ...
连接mysql并查询
1.将mysql-connector-java-5.1.7-bin.jar放入Jmeter安装目录的bin文件夹中 2.在顶层目录<测试计划>中加载驱动 3.添加JDBC Connecti ...
mysql 远程连接报错
./mysql -uzhu -p -h192.168.1.200 ERROR 2003 (HY000): Can't connect to MySQL server on '192.168.1.200 ...
分布式唯一ID实现
ID生成的核心需求全局唯一趋势有序为什么要全局唯一避免ID冲突著名的例子就是身份证号码,身份证号码确实是对人唯一的,然而一个人是可以办理多个身份证的,例如你身份证丢了,又重新补办了一张,号码 ...
AM8不能下任何载附件及所有聊天记录无法登记
问题描述: 接收附件时,点击打开或者下载都不成功,但可以发送消息和附件.但在消息管理器中,也查询不到发送和接收的消息原因分析:此问题是windows开机登录用户权限问题(若登录的账号是 whx), ...
Estimation
Estimation 给出一个长度为n序列$\{a_i\}$,将其划分成连续的K段,对于其中一段$[l,r]$,设其中位数为m,定义其权值为$\sum_{i=l}^r|m-a_i|$,求最 ...
js实现获取选中checkbox的值
var bookVersionId = []; var examVirtualSetResultId; $.each($('input[type=checkbox]:checked'),functio ...
ArcGIS Server 10.x查询管理用户名和修改管理员密码
在x:\Program Files\ArcGIS\Server\tools\passwordreset下有个bat文件,用管理员用户运行它. PasswordReset -l PasswordRese ...
JVM之类加载过程
# 类的生命周期 1. 加载 loading2. 验证 verification3. 准备 preparation4. 解析 resoluation5. 初始化 initialization6. 使用 ...

逻辑回归代码demo

逻辑回归代码demo的更多相关文章

随机推荐

热门专题