洛谷P3645 [APIO2015]雅加达的摩天楼

题目描述

印尼首都雅加达市有 N 座摩天楼，它们排列成一条直线，我们从左到右依次将它们编号为 0 到 N − 1。除了这 NN 座摩天楼外，雅加达市没有其他摩天楼。

有 M 只叫做 “doge” 的神秘生物在雅加达市居住，它们的编号依次是 0 到 M − 1。编号为 i 的 doge 最初居住于编号为 Bi 的摩天楼。每只 doge 都有一种神秘的力量，使它们能够在摩天楼之间跳跃，编号为 i 的 doge 的跳跃能力为 Pi （Pi>0）。

在一次跳跃中，位于摩天楼 b 而跳跃能力为 p 的 doge 可以跳跃到编号为 b − p （如果 b − p < N）或 b+p（如果0≤b+p<N）的摩天楼。

编号为 0 的 doge 是所有 doge 的首领，它有一条紧急的消息要尽快传送给编

号为 1 的 doge。任何一个收到消息的 doge 有以下两个选择:

跳跃到其他摩天楼上；

将消息传递给它当前所在的摩天楼上的其他 doge。

请帮助 doge 们计算将消息从 0 号 doge 传递到 1 号 doge 所需要的最少总跳跃步数，或者告诉它们消息永远不可能传递到 1 号 doge。

输入输出格式

输入格式：

输入的第一行包含两个整数 N 和 M。

接下来 M 行，每行包含两个整数 Bi 和 Pi。

输出格式：

输出一行，表示所需要的最少步数。如果消息永远无法传递到 1 号 doge，输出 −1。

输入输出样例

输入样例#1：

输出样例#1：

说明

【样例解释】

下面是一种步数为 5 的解决方案：

0 号 doge 跳跃到 2 号摩天楼，再跳跃到 4 号摩天楼（2 步）。

0 号 doge 将消息传递给 2 号 doge。

2 号 doge 跳跃到 3 号摩天楼,接着跳跃到 2 号摩天楼，再跳跃到 1 号摩天楼（3 步）。

2 号 doge 将消息传递给 1 号 doge。

【数据范围】

所有数据都保证 0≤Bi<N。

子任务 1 （10 分）1≤N≤10

1≤Pi≤10

2≤M≤3

子任务 2 （12 分）1≤N≤100

1≤Pi≤100

2≤M≤2000

子任务 3 （14 分）1≤N≤2000

1≤P≤2000

2≤M≤2000

子任务 4 （21 分）1≤N≤2000

1≤Pi≤2000

2≤M≤30000

子任务 5 （43 分）1≤N≤30000

1≤Pi≤30000

2≤M≤30000

题解：

哇哇哇这道题A掉真不容易

这道题看到就想着建图，但是直接建肯定是不行的。

为啥不行呢？原来，对于某一个doge的p值，我们的建图方法是这样滴：

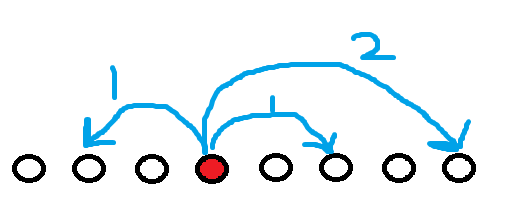
如果p值较大的话，那还好办，因为不会连出去多少边

但是，如果p值小的话，那么每一个点可能会往外连好多个边，而且可能有重复的！

复杂度可能接近 n² 哦

那么，如何改进建边方法？

老师教我们做分层图（似乎也叫分块？并不太清楚……）

对于p值较大的，比如大于sqrt(n)的，我们还直接建边

但是对于p值较小的，我们就对于不同的p值分别建图，然后每两个可一步到达的“相邻”点间都连正反两条边

就像这样：

p=1层的图:

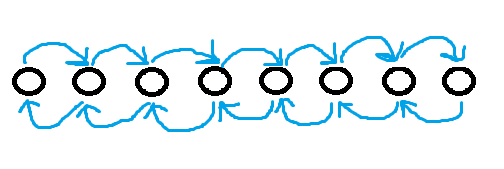
p=2层的图：

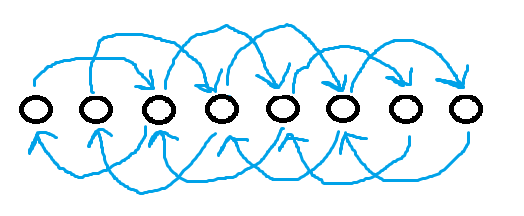
（画图好累……）

好了大概层里建图就是这样

可是不能光在一个层里面跑啊，得在不同层间跑

那么不同层间的边怎么连？

不同层间的边其实就相当于一栋楼中有些可跳距离不同的doge，那对于每一个doge都把同一个点不同层的点指向该点（这样说好抽象啊……看代码应该好理解些）

这样建图复杂度是nlogn的

这样图建完后跑最短路就可以了

我一开始用dijkstra堆优化，但是始终T一个点。后来改成SPFA又修改了许多耗时的地方才A掉……95分了好长时间……

我做这道题时中间有一段时间一直65分，因为我在建图时有一块儿想错了

我把p值较大的暴力建图时是按照p值较小的建图方法建的（如上2图）

但是这样是有问题的

两者的区别不单是前者边少后者边多，更是前者只能从一个点出发去其他点，而后者可从每一个点出发去其他点！

虽然感觉上求两点之间距离这两种方法是一样的，但当有其他点、边或其他操作插进来后就很不一样了

比如前一个图，第三个点与第四个点是无法互相到达的，而在后面图中就可以

下次写题是一定要注意这一点！要想清楚了！

代码：

 #include<cstdio>

 #include<iostream>

 #include<algorithm>

 #include<math.h>

 #include<queue>

 #define INF 1000000007

 using namespace std;

 const int MAXN = ;

 struct node{

     int v,len,lev;

     node *next;

 }pool[*MAXN],*h[][MAXN];

 int cnt;

 int read(){

     int x=,f=;

     char ch=getchar();

     while(ch>'' || ch<'') ch=getchar();

     while(''<=ch && ch<='') x=x*+ch-'',ch=getchar();

     return x;

 }

 void addedge(int u,int lu,int v,int lv,int len){

     node *p=&pool[++cnt];

     p->v=v;p->len=len;p->lev=lv;

     p->next=h[lu][u];h[lu][u]=p;

 }

 int n,m,sn;

 int b[MAXN],p[MAXN],vis[];

 int d[][MAXN],use[][MAXN];

 struct qqq{

     int num,lev;

 };

 queue<qqq> que1;

 void spfa(int S,int lS,int T){

     int u,v,l;

     qqq newq,now;

     for(int i=;i<sn;i++)

         for(int j=;j<n;j++) d[i][j]=INF;

     while(!que1.empty()) que1.pop();

     d[lS][S]=;

     newq.num=S;newq.lev=lS;

     que1.push(newq);

     while(!que1.empty()){

         now=que1.front();que1.pop();

         u=now.num;l=now.lev;

         for(node *p=h[l][u];p;p=p->next)

         {

             v=p->v;

             if(d[p->lev][v]>d[l][u]+p->len){

                 d[p->lev][v]=d[l][u]+p->len;

                 if(use[p->lev][v]) continue;

                 newq.num=v;newq.lev=p->lev;

                 que1.push(newq);

                 use[p->lev][v]=;

             }

         }

         use[l][u]=;

     }

 }

 int main()

 {

     int i,j,l2,S,T,lS;

     n=read();m=read();

     for(i=;i<m;i++) b[i]=read(),p[i]=read();

     sn=min((int)sqrt(n),);

     S=b[];T=b[];

     if(p[]<sn) lS=p[];else lS=;

     //addedge

     for(i=;i<m;i++){

         if(p[i]>=sn){

             vis[]=;

             for(j=b[i]%p[i];j<n;j+=p[i]){

                 if(j==b[i]) continue;

                 addedge(b[i],,j,,abs(j-b[i])/p[i]);

             }

         }

         else vis[p[i]]=;

     }

     for(i=;i<sn;i++)

         if(vis[i]){

             for(j=;j+i<n;j++){

                 addedge(j,i,j+i,i,);

                 addedge(j+i,i,j,i,);

             }

         }

     //level

     for(i=;i<m;i++){

         if(p[i]<sn) l2=p[i];

         else l2=;

         for(j=;j<sn;j++)

             if(j!=l2 && vis[j]){

                 addedge(b[i],j,b[i],l2,);

             }

     }

     //spfa

     spfa(S,lS,T);

     int ans=INF;

     for(i=;i<sn;i++) ans=min(ans,d[i][T]);

     if(ans==INF) printf("-1\n");

     else printf("%d\n",ans);

     return ;

 }