cs231n学习笔记——lecture6 Training Neural Networks

该博客主要用于个人学习记录，部分内容参考自：[基础]斯坦福cs231n课程视频笔记(三) 训练神经网络、【cs231n笔记】10.神经网络训练技巧(上)、CS231n学习笔记-训练神经网络、整理学习之Batch Normalization（批标准化）、CS231n-2022 Module1: 神经网络3：Learning and Evaluation

一、激活函数Activation Funnctions

1、Sigmoid： \(\sigma(x)=\frac{1}{1+e^{-x}}\)

• 每个输入到Sigmoid函数中的元素都会被压缩到[0,1]范围内。如果输入值很大，会得到一个接近1的输出；如果输入是一个绝对值很大的负值，在横坐标接近于0的区域，我们可以将这部分看作线性函数
• 曾经被看作是神经元的饱和放电率
• 3个问题：
  • 饱和神经元将使梯度消失
    
    当输入远远离0时，处于饱和区，激活节点的本地梯度趋近于0，导致前面的层中参数无法得到有效的更新。
  • Sigmoid的输出不是关于0对称的。
    
    意味着如果输出的激活值作为后继节点的输入一直是正数，那么导致后续节点本地梯度（就是w对应相乘的那个x）一直是正数，所以所有输入的下游梯度一定和输出的上游梯度同号，全为正或全为负(具体依表达式f而定)，这会导致参数用梯度下降法更新时，呈现z字型下降。 正如下图中所示，最好的路径是蓝色，但是由于受到方向限制，只能通过反复的红色路径才能达到同样效果，使得梯度更新效率低。
    
    
  • 指数运算消耗大量计算资源。

2、tanh(x)双曲正切

• 比Sigmoid好，但是仍存在问题。
• 输出关于0对称，不存在zig zag path问题。
• 饱和时依然会出现梯度消失问题，在这些区域中依然能看到梯度是平的，因此会阻碍梯度传递。

3、ReLU： \(f(x)=max(0,x)\)

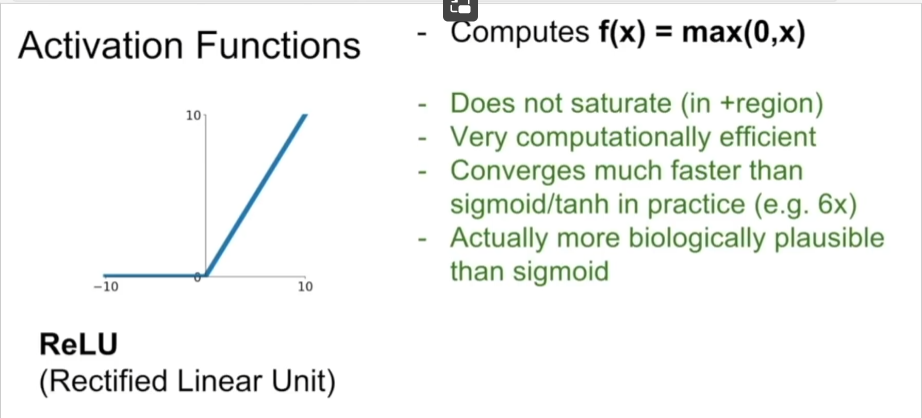
• 不以0为中心
• 具有饱和的问题，在输入x落在负半轴时，输出总是零，从而参数的梯度反传时得到的为零
• x<0时，梯度消失，把这个现象称为dead ReLU

Dead ReLU Problem

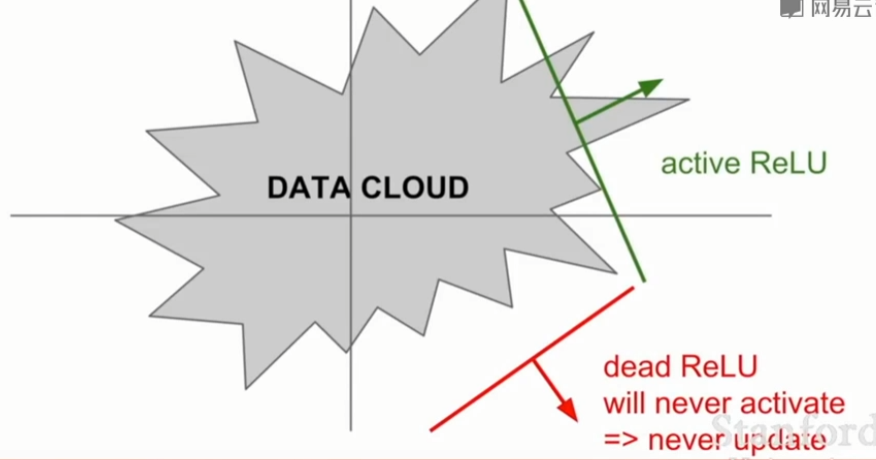
• 大多数输入为负时，经过激活后归零，负输入不能得到梯度，负输入的权重因此不能被更新。
• 产生原因：

  • 参数初始化问题。
    
    如果权重设置太低，恰巧不在data cloud中，这导致我们将不能得到一个能激活神经元的数据输入，同时也不会有一个合适的梯度传回来，所以它既不会更新，也不会被激活。

  • 学习率太高导致在训练过程中参数更新太大。
    
    当你的学习率很大时，在这种情况下从一个ReLU函数开始，但因为你在进行大量的更新，权值不断波动，然后ReLU单元会被数据的多样性所淘汰，这些会在训练时发生，在开始时很好，但在某个时间点之后开始变差最后dead。

• 在实际中，如果冻结了一个已经训练好的网络，然后传数据进去，可以看到实际上网络中多达10%到20%的部分是这些dead ReLUs。大多数使用ReLU的网络都有这类问题，但还能用作训练网络。

4、Leaky ReLU： \(f(x)=max(0.1x, x)\)

• 基于ReLU的改进，与ReLU唯一不同的是，ReLU在负区间中保持水平，Leaky ReLU在负区间上有微小的斜率，所以不存在饱和的问题；
• 计算效率高；
• 在实践中收敛速度比Sigmoid/tanh快；
• 没有die的问题。

5、ELU (Exponential Linear Units): \(f(x)= \left\{\begin{array}{lrc}x&if&x>0\\\alpha(exp(x)_1)&if&x\leq0\end{array}\right.\)

• 有ReLU所有的优点
• 接近0的平均输出
• 在负区间上建立了一个负饱和机制，没有斜率，这里有些具有争议的观点认为这样使得模型对噪音具有更强的鲁棒性以此得到更健壮的反激活状态

6、Maxout Neuron： \(f=max(w_1^Tx+b_1,w_2^T+b_2)\)

• 结合了ReLU和Leaky ReLU,线性函数、不会出现饱和性梯度消失，不会出现多数梯度变0的情况
• 问题是每个神经元的参数数量会翻倍

总结

• 使用ReLU要注意学习率不要选太大
• 尝试使用Leaky ReLU/Maxout/ELU
• 可以尝试使用tanh，但是效果可能不太好
• 不要轻易使用sigmoid

二、数据预处理 Data Preprocessing

在训练开始之前，我们常常会对数据进行预处理，以使得更加适合训练。测试时，或者实际运行时，不用做数据预处理（当然这里说的是类似归一化、zero-centerd这样的操作，反之，像截取这样的处理还是要的）。

归一化就是将原本散乱的数据归一成零均值、方差为1，zero mean ,unit variance的操作，由此数据的中心大致处于D维空间的零中心。归一化可以使得分类器更鲁棒，对于微小的扰动不会过于敏感。

在一般的机器学习问题会有差别很大的特征，并且这些特征会处于的范围差别也很大，所以需要使用归一化。

在本课程中，一般对图像来说，在每个位置已经得到了相对可比较的范围与分布，所以大多数情况下我们会做zero centering的处理，但不会真的过多地归一化像素值。

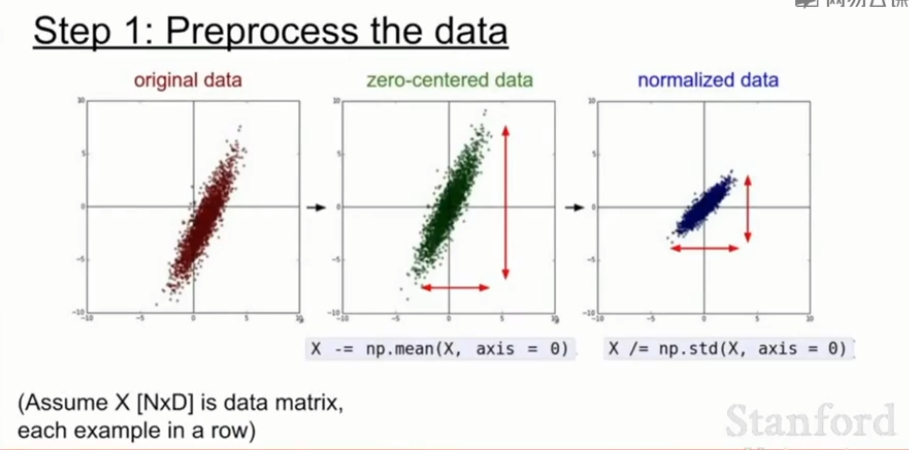
在机器学习中，可能会看到有PCA和白化的数据预处理方式。但在图像应用领域中，我们做零均值化（zero mean） 的处理而不做归一化，也不会做这些更复杂的预处理，因为对于图像来说，我们不会真的想要所有的输入，我们就想在空间中应用卷积神经网络得到原图像的空间结构。

零均值化（zero mean）的处理。

在训练阶段我们从所有图像中计算它们的均值，得到与每张图像尺寸相同的均值图像，对要传到网上的每张图减去整张均值图像的值。在测试阶段对在训练中确定的数组做同样的事。

在实践中，对一些网络，我们也可以通过减去单通道均值代替用一整张均值图像来将图像集零中心化，我们只是取每个通道的均值。这么做是因为发现纵观整张图像来看相似度足够，减去均值图像和只是减去单通道值二者相比没有太大的不同，并且更容易传送和处理。所以你也会在像是VGG网络中见到这种操作。

三、初始化权重 Weight Initialization

权重初始化的主要目的，是为了让数据更好地分布，如果数据大量集中在一个部位，很可能导致梯度丢失，从而无法更新前面的权值。

如果把所有参数都设为0，给定一个输入，每个神经元将在你的输入数据上做相同操作，输出相同的值，得到相同的梯度，这与我们期望的不同神经元学习到不同的知识相悖。关键就是当用相同值初始化所有参数时，基本没有打破参数对称问题。

若所有权重是一个从概率分布中抽样的小的随机数， \(W = 0.01 * np.random.randn(D,H)\)。在这个例子中从高斯分布中抽样，对它进行缩放使标准差为0.01，由此给定了很多小的随机参数。这样的参数适用于小型网络中，打破了参数对称问题，但在结构深一些的网络中可能会存在问题。

例如我们初始化一个10层神经网络，每层有500个神经元，使用tanh非线性激活函数，用小的随机数来初始化，经过网络在每一层观察产生的激活函数的数据的统计结果，如果计算每一层的均值和标准差会发现在第一层中能得到较为合理的高斯分布，接着不断收缩，最后所有的激活值都变成了0。在反向传播时，权重的梯度由上游梯度×本层梯度得到，即\(W·X\)，由于输入的X很小，权重的梯度将会很小，基本没有更新，最终都趋向于0。

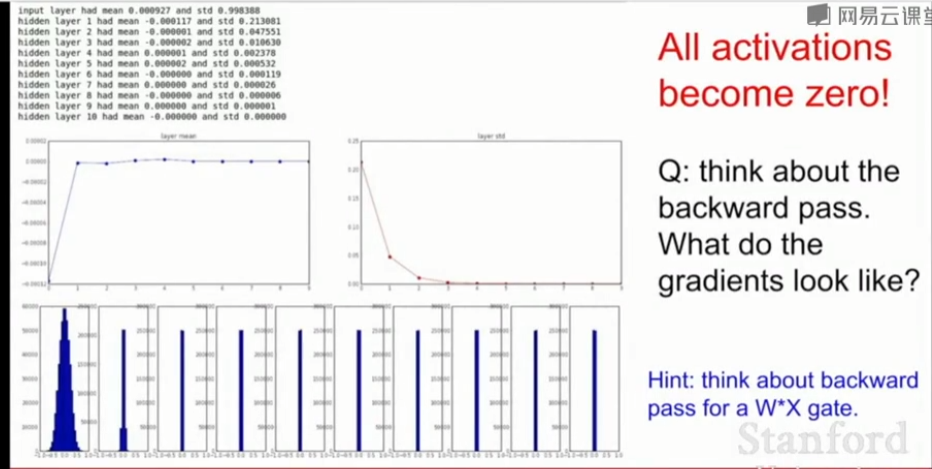
若用1代替0.01，即\(W = 1 * np.random.randn(D,H)\)。由于权重变大了，所以几乎所有神经元都处于饱和状态，无论tanh的负方向还是正方向，在实践中观察每一层激活值的分布，它们会趋近于-1或+1，对照前面讲过的tanh，将导致所有梯度趋于0，权重得不到更新。

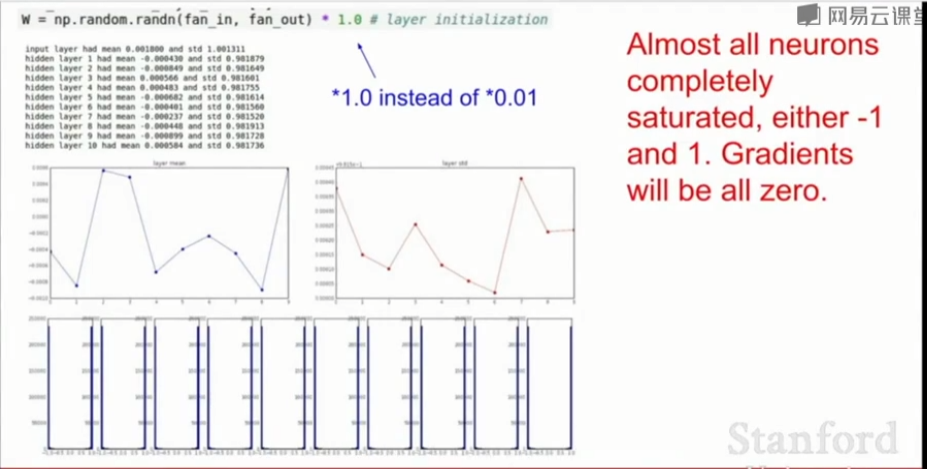
权重太小，激活值趋近于0，梯度趋于0，不学习。

权重太大，网络饱和，梯度也趋于0，不学习。

Xavier 初始化: \(W = np.random.randn(Din, Dout) / np.sqrt(Din)\)

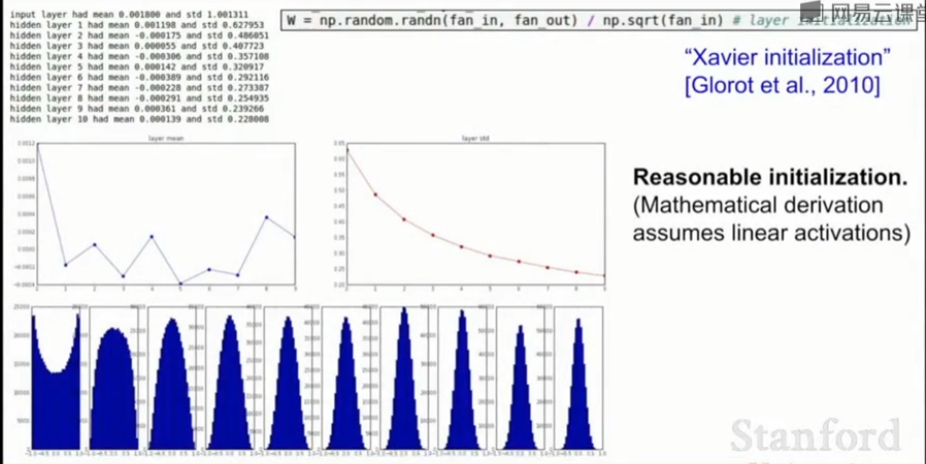
从标准高斯分布中取样，根据我们拥有输入的数量来进行缩放，要求输入的方差等于输出的方差。

如果输入数据少，将除以较小的数，从而得到较大的权重，我们需要较大的权重来得到一个相同输出的方差。

反之，如果输入数据多，将除以较大的数，得到较小的权重来得到一个相同输出的方差

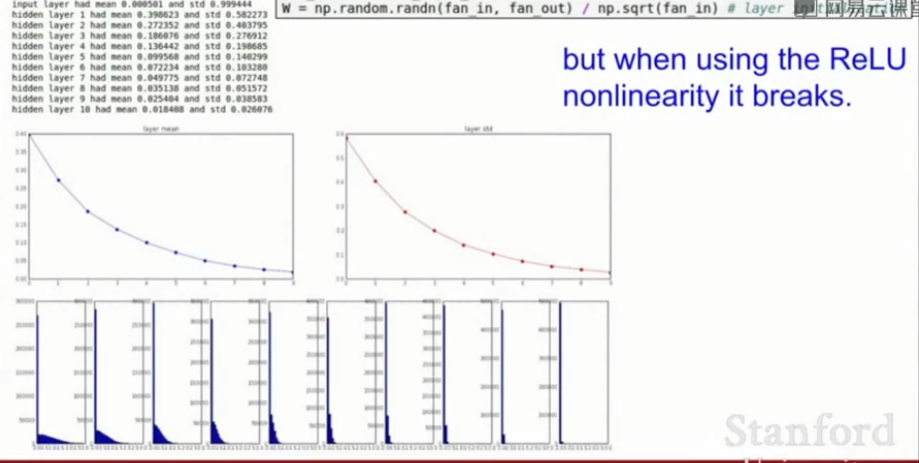
但是当使用ReLU激活函数时，它会消除一半的神经元，实际上会把得到的方差减半，可以将公式变为\(W = np.random.randn(Din, Dout) / np.sqrt(Din / 2)\)

四、批量归一化Batch Normalization

Batch normalization 的 batch 是批数据，把数据分成小批小批进行随机梯度下降 ，而且在每批数据进行前向传递的时候, 对每一层都进行 normalization的处理。常用在在全连接层FC或者卷积层Conv之后，非线性层之前。随着网络的深度增加，每层特征值分布会逐渐的向激活函数的输出区间的上下两端（激活函数饱和区间）靠近，这样继续下去就会导致梯度消失。BN就是通过方法将该层特征值分布重新拉回均值为0方差为1的标准正态分布，特征值将落在激活函数对于输入较为敏感的区间（把输入限制在非线性函数的线性区域内），输入的小变化可导致损失函数较大的变化，使得梯度变大，避免梯度消失，同时也可加快收敛。

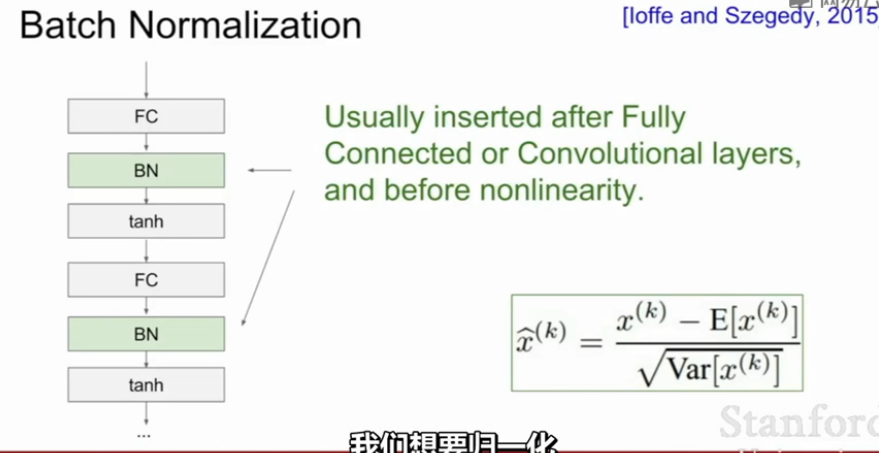
BN做法

• 独立计算每个维度的经验平均值和方差（对于每个小批次）
• 归一化Normalization：\(\hat{x}^{(k)}=\frac{x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}\)
• 缩放和平移：\(\hat{y}=\gamma ^{(k)}\hat{x}^{(k)}+\beta ^{(k)}\)
  • normalization后当于把非线性激活函数替换成线性函数了，数据趋向标准正态，会导致网络表达能力变差。所以BN为了保证非线性的获得，对变换后的满足均值为0方差为1的x又进行了缩放和平移操作，使得标准正态分布有些偏移，变得不那么标准了。\(\gamma\)和$ \beta$都是神经网络自己学习的。

给定输入，对每个输入的小批量都计算均值和方差，利用均值和方差进行归一化操作，然后用常量\(\gamma\)进行额外的缩放，再用另一个因子\(\beta\)进行平移，这里实际在做的是允许你恢复恒等函数。从而改进了整个网络的梯度流，具有更高的鲁棒性，能够在更广范围的学习率和不同初值下工作，所以一旦使用批量归一化，训练会更容易。

在测试阶段，对批量归一化层，现在减去了训练数据中的均值和方差，所以在测试阶段不用重新计算，只需把这当成训练阶段，例如在训练阶段用到了平均偏移，在测试阶段也同样会有所用到。

好处：

• 改善网络中的梯度流；
• 允许更高的学习率、更快的收敛；
• 减少对初始化的依赖；
• 作为正则化的一种形式，因为每层的每个激活值和这些输出，都来源于输入X以及批中被采样的其他样本，你将通过这一批样本的经验化均值对输入数据进行归一化，它不再对给定的训练样本提供确定性的值，而是将这些输入放入批中，所以它不再是确定值，就像X中加入一些抖动，从而实现正则化的效果。

五、训练过程监视Babysitting the Learning Process

1、数据预处理Preprocess the data

2、choose the architecture

3、优化前：

• Look for correct loss at chance performance. 确保用很小的值进行参数初始化时得到符合预期的损失。最好先单独检查数据损失(将正则化强度设置为零)。例如，对于具有Softmax分类器的CIFAR-10，我们期望初始损失为2.302，因为我们期望每个类的扩散概率为0.1（因为有10个类），并且Softmax损失是正确类的负对数概率，所以：-ln(0.1)=2.302。如果检验时没有获得预期损失，那么初始化可能会出现问题。

• 作为第二个完整性检查，经过上一步的初次检验后，增加正则化强度时，损失也应该随之增加。

• 过拟合测试Overfit a tiny subset of data.在对整个数据集进行训练之前，试着对一小部分数据(例如20个样本)进行试训练，确保你可以得到zero cost。在这个实验中，应该将将正则化设置为零，否则会影响你获得0损失。如果没有通过这个检验，则该网络模型就不值得继续使用完整的数据集进行训练。

4、开始训练

在神经网络的训练过程中，有许多有用的量需要监控：loss, train/val accuracy, ratio of the update magnitudes, the first-layer weights in ConvNets

• 取所有训练数据，加上一个小的正则化项，找到使损失降低的学习率：[1e-3, 1e-5]
  • 如果损失没有下降，意味着学习率太低；如果损失为NaN，则意味着学习率高
  • 如果训练精度和验证精度之间存在很大差距，这意味着过拟合（可以增加正则化或获取更多数据）；如果没有差距，这意味着可以增加模型容量。
  • 如果准确性仍在提高，你需要更长时间的训练

5、提前停止：当验证损失开始上升时

六、超参数优化Hyperparameter Optimization

• Learning rate（最重要，首先要处理）, regularization, learning rate decay, model size

• 一重验证比交叉验证好

• 交叉验证
  
  在训练集上训练，在验证集上验证，观察这些超参数的实验效果。

  • 先粗搜索、然后再精搜索：
    
    ①首先选择相当分散的数值，用几个Cross-validation 迭代学习来确定超参数的有效范围，以便做出调整
    
    ②花较长时间在前面得到的超参数区间内进行进一步精确搜索
    
    如果出现一个远大于初始cost的值比如超过了3倍，可以说明这个超参数是错的，它会迅速变得很大，直接结束训练。
  • 在对数上搜索超参数： \(learning_rate = 10 ** uniform(-6, 1)\)
  • 但有些参数是按原始比例搜索的： \(dropout = uniform(0,1)\)

• 随机搜索有时比网格搜索更好.超参数最优值大概率并不会恰好出现你规划的搜索格点上。随机搜索能帮助你更精确地找到最优解。
  
  

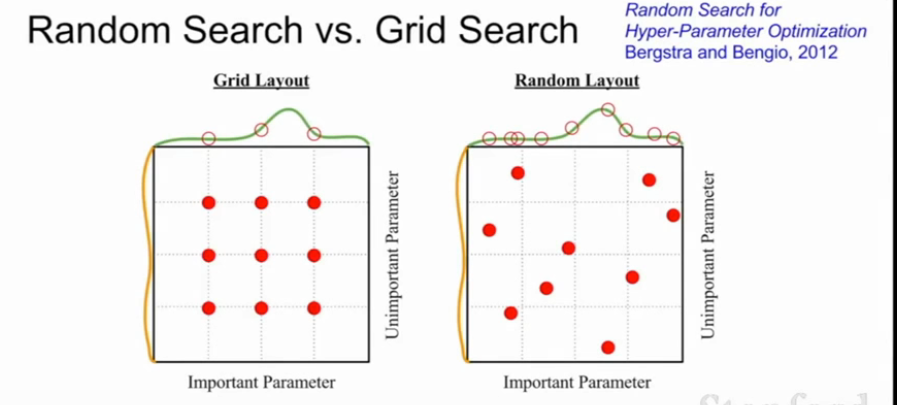
  • 确保最优值不在搜索区间的边界

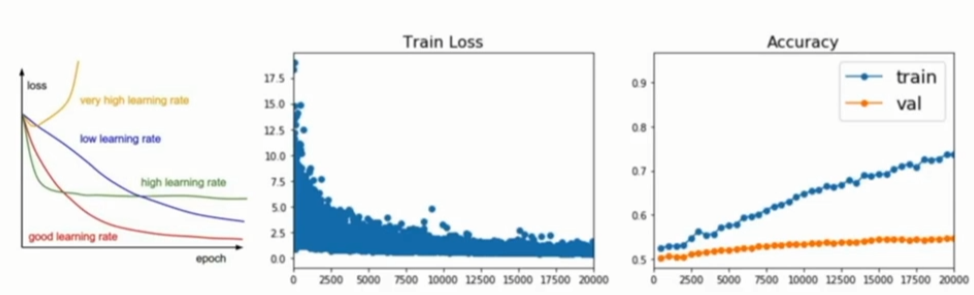
• 左图是随时间变化的损失函数曲线，由图中发现曲线在下降，说明神经网络的损失函数在降低。中间的图中，x轴是训练时间或迭代次数，y轴是模型在训练集上的损失函数。右图是训练集和测试集随时间变化的精确度。可以发现随着时间的增加，训练集上的效果随着损失函数的下降越来越好，但验证集却在达到某一点后不再上升，这表明模型进入了过拟合状态，这时可能就需要加入其他的正则化手段。
  
  

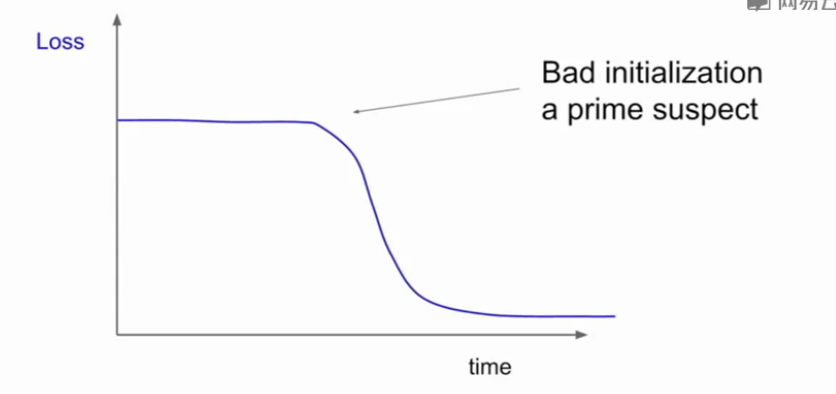
• 当观察学习率损失取消时，如果在一段时间内很平缓突然又开始训练，可能是初值没有设置好