week_8

Andrew Ng 机器学习笔记 ---By Orangestar

Week_7_Unsupervised Learning

While supervised learning algorithms need labeled examples (x,y), unsupervised learning algorithms need only the input (x). You will learn about clustering—which is used for market segmentation, text summarization, among many other applications.We will also be introducing Principal Components Analysis, which is used to speed up learning algorithms, and is sometimes incredibly useful for visualizing and helping you to understand your data.

---

1. Unsupervised Learning: Introduction

第一个无监督学习算法

no labels!

送入算法，并得到数据的结构。大致就是这样



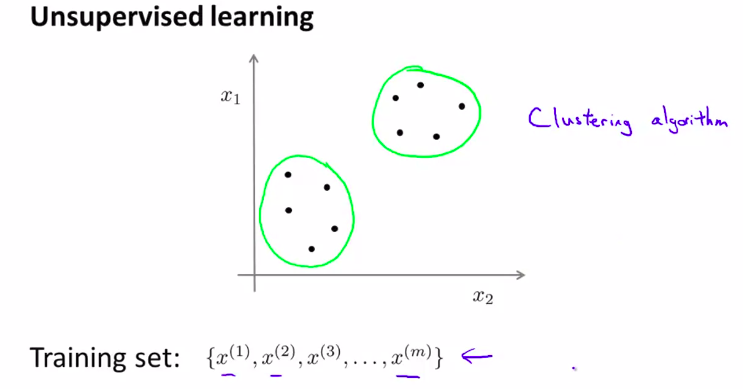
其中一种类型 就是： 聚类 cluster

2. K-Means Algorithm

K均值算法，它是一种迭代方法。将数据分为几个簇或者集

1. 选出两个点，叫做聚类中心。这意味着把数据分为2类

2. 然后K均值算法要做2件事情

   1. 簇分配
   2. 移动聚类中心

详细通俗解释：

1. 在K均值算法的每次循环中 ，第一步是要进行簇分配 ,这就是说 ,我要遍历所有的样本 ,就是图上所有的绿色的点 ,然后依据 ,每一个点是更接近红色的这个中心 ,还是蓝色的这个中心 .来将每个数据点 .分配到两个不同的聚类中心中 .具体来讲，就是对数据集上的所有点，依据他们更接近红色中心，还是蓝色中心。如下图
   
   

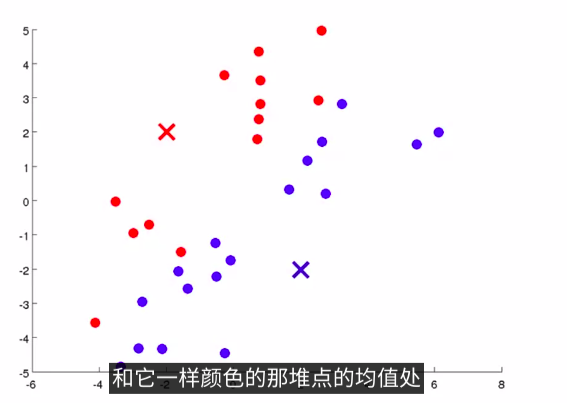
2. 然后，我们需要移动聚类中心。具体的操作方法 是这样的 我们将两个聚类中心 也就是说红色的叉 和蓝色的叉 移动到 和它一样颜色的那堆点的均值处 那么我们要做的是 找出所有红色的点 计算出它们的均值 就是所有红色的点 平均下来的位置 然后我们就把红色点的聚类中心移动到这里 蓝色的点也是这样 找出所有蓝色的点 计算它们的均值 把蓝色的叉放到那里 如下图：
   
   

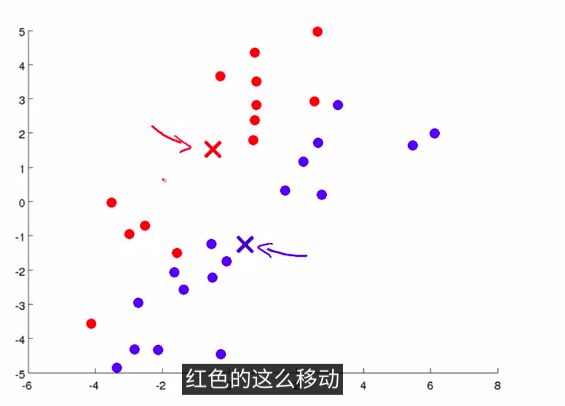
3. 这样就会进入另一个簇分配。逐步循环。一直迭代下去，最后，收敛后，就会发现已经分好了：如下图：
   
   

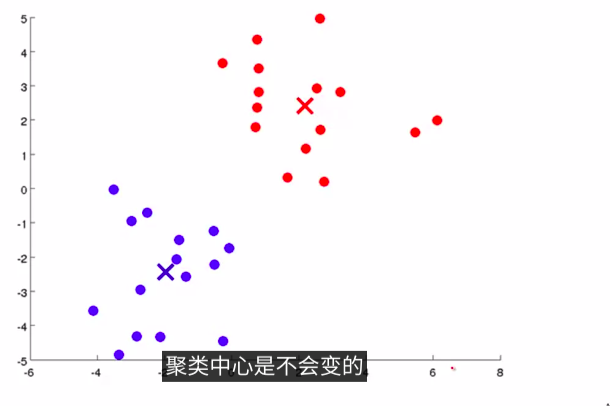
然后，我们用更标准的语言来详细介绍一下K均值算法：

• 首先，我们需要：
  
  

  K是我们要分为多少个簇。前提准备工作完成后

• 然后：
  
  进行簇分配和移动聚类中心
  
  

  注意：如果遇到了没有点分配给它的聚类中心。我们所要做的，就是重新随机找一个聚类中心，但是直接移除那个中心是更为常见的方法。但是，这样的例子并不常出现。

再讨论一个，遇到了没有分开的聚类怎么办？

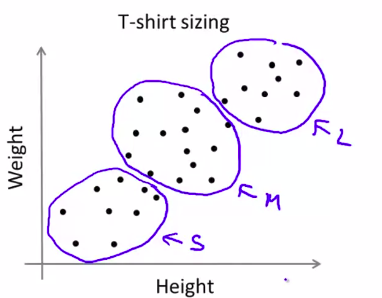
T-shirt的分类，确定s,m,l号码是怎么样的聚类？如何使用k

均值算法？

3. Optimization Objective优化目标函数！

先理解 什么是 k均值算法 的 优化目标函数

当k均值在运行的时候，我们将对两组变量进行跟踪

然后，我们就可以提出优化函数了：

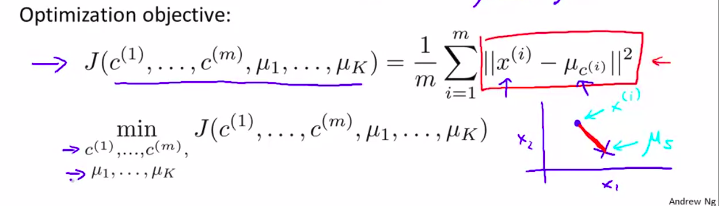
所以，k均值算法要做的事情就是，它将找到参数c(i) 和 μi，在这个代价函数（也叫失真代价函数distortion cost function） 的最小值。

更详细解 释：

详细理解失真函数，其实就是聚类中心分类的依据

4. Random Initialization

如何初始化。这将讨论如何避开局部最优来构建k均值聚类方法

其中一种方法是靠人品：

随机选择样本来当做聚类中心

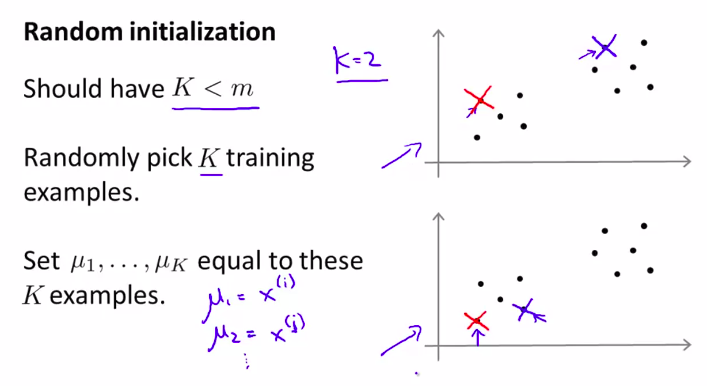
但是，如果随机选择的聚类中心，落到了局部最优上，怎么办？

如图所例：

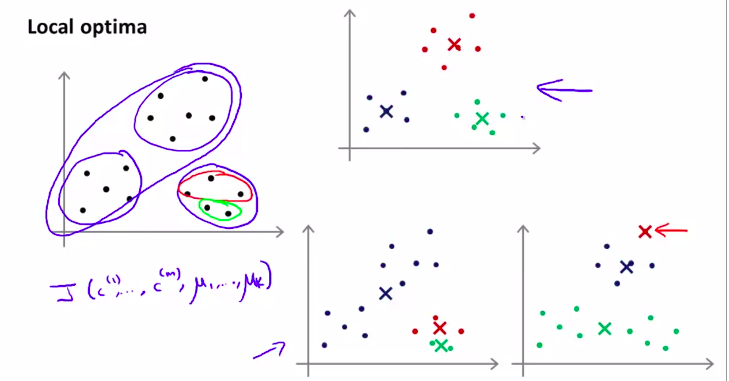
其中一个解决这种问题的方法就是简单粗暴：只要多次初始化，多次运行k均值算法就行了!

然后，在多次运行的结果中选择最优的！

注;这种方法在聚类数目较小的目标中，效果十分好，但是聚类一多，可能就会差强人意

（多次随机初始化）

5. How to choose K/the Number of Clusters

多数靠可视化，也就是靠看！多数还是靠手动

但是靠可视化来确定是模棱两可的，所以难以有一个自动化的方法来确定

• Elbow Method（肘部法则）
  
  

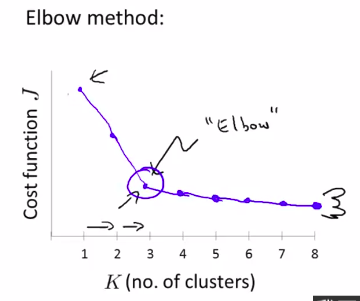
  但是事实并不会总是和人所愿。有的时候我们依然会得到一个模棱两可的图线。
  
  

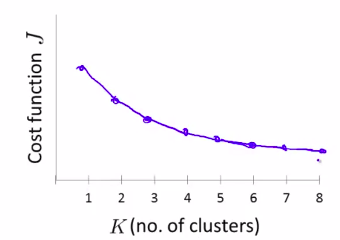
  但是它是一个值得期待的方法。可是并不能普遍很好的应用

• 例子：

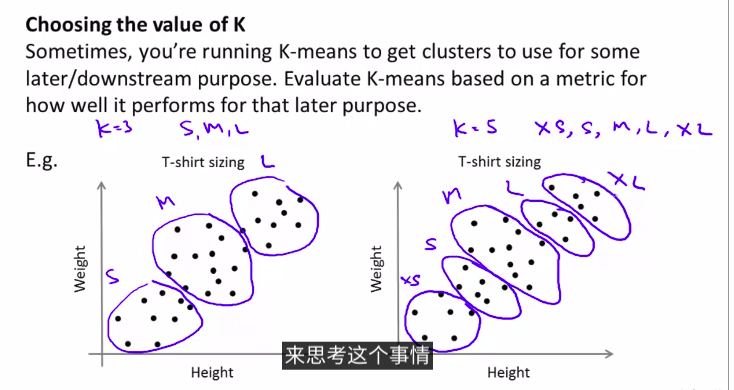
这是从实际例子来思考如何选择k

所以，更好的方法是从实际角度和后续应用来看如何选择K

---

1. Motivation I : Data Compression

接下来我们要学习第二种无监督学习问题，它叫做维数约减（dimensionality reduction）

这个算法的其中一个应用就是数据压缩

接下来我们简单介绍维数约简：

例子：数据压缩降维。

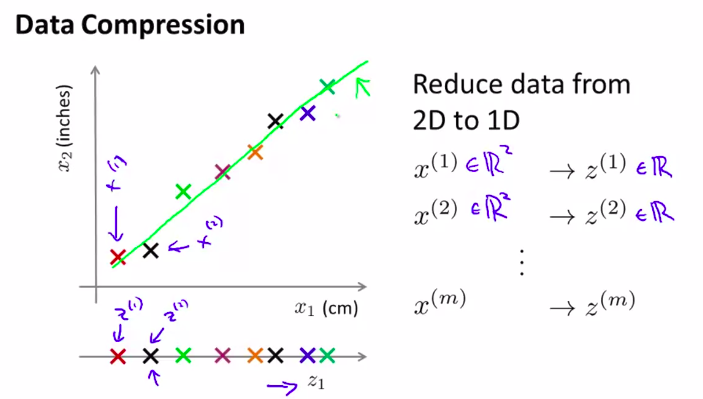
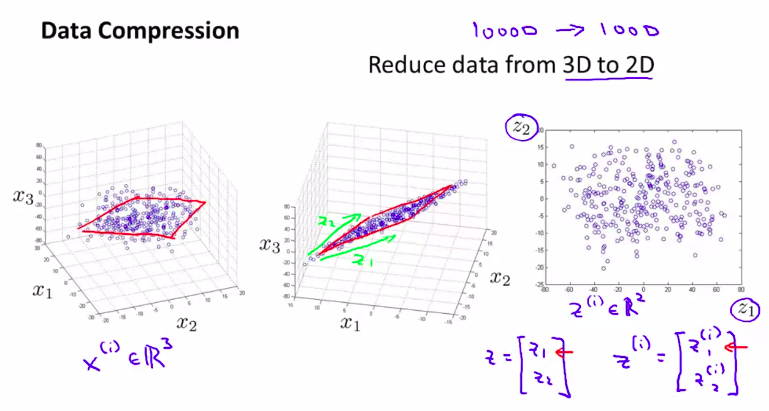
当然这是数据的粗略处理

2. Motivation II: Visualization

第二种数据降维的应用： 可视化数据

那一般都要降维到2或者3维。只有与这样才能可视化

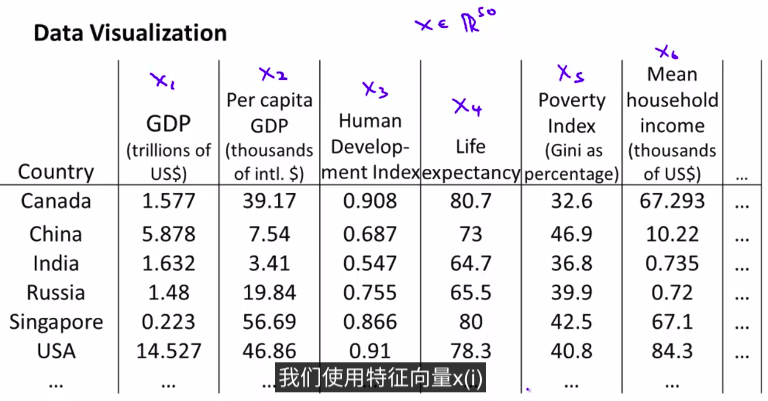
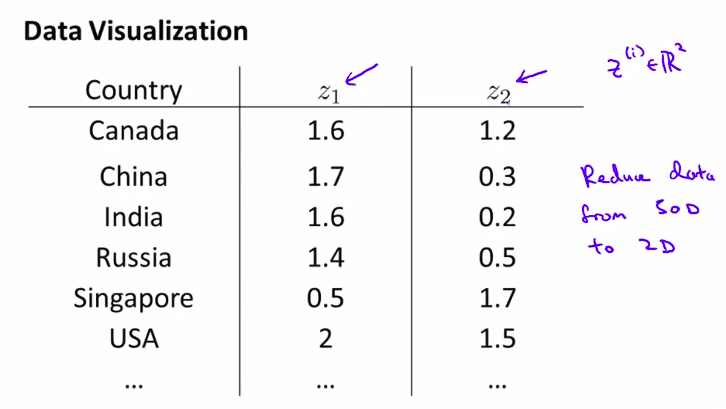
3. Principal Component Analysis Problem Formulation ( PCA算法 )

对于降维问题来说，目前最常用，最流行的算法是：主成分分析法。（Principal Component Analysis ）(PCA)

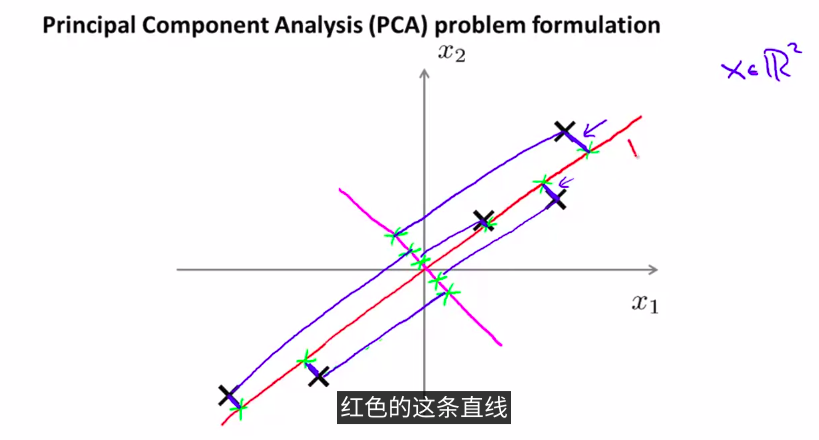
我们先从2维降到1维这个例子来理解

如图，将数据投影到一条线上，并使数据到这条线上的距离达到最小。也就是这蓝色线段的长度达到最小。当然，这些蓝色线段的长度，通常被叫做 投影误差。

在应用PCA之前，通常的做法是先进行均值归一化和特征规范化。

（品红色这条线是反例，算法并不会选择这条差的线）

正式一点描述：

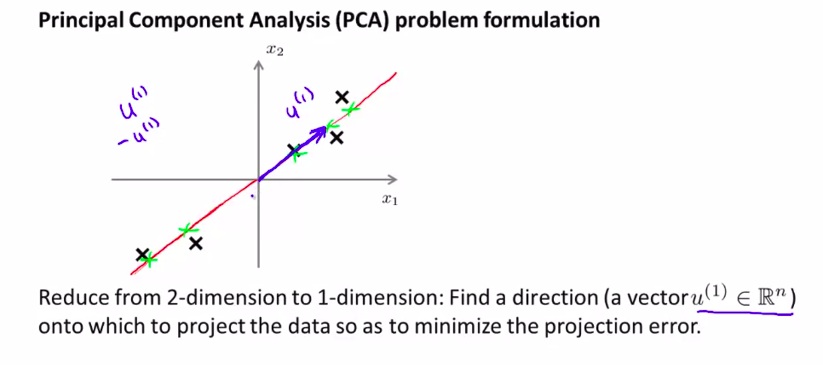
就是要得到一条直线，使向量投影最小

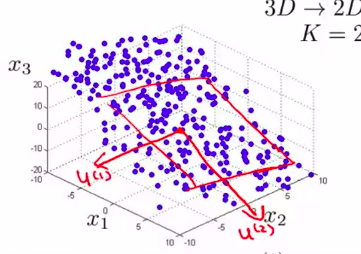
推广到N维就是：

当然，3D到2D就是：

把三维的数据投影到一个平面。

在2维情况下，PCA有一点像线性回归

但是，他们是两种不同的算法！！！

注意不同，如图：

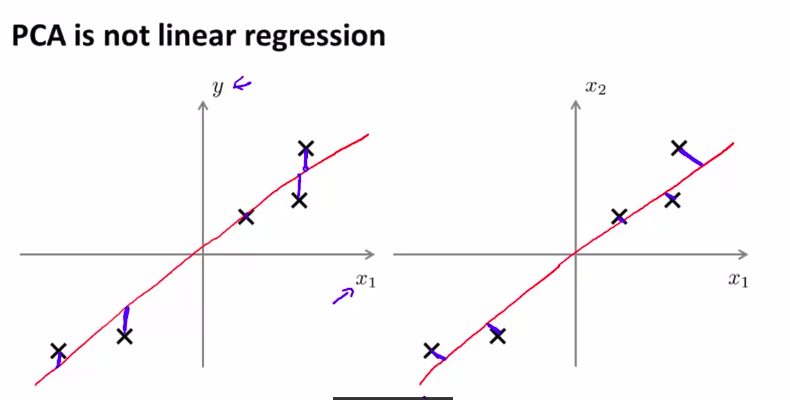
他们两个所拟合的直线，的原则不同！

而且，PCA没有y来制约。

x所有都是均等的。平等的。

所以。PCA是寻找一个低维的平面，对数据进行投影，以便最小化投影误差的平方，最小化每个点与投影后的对应点之间的距离的平方值。

下一节我们将学习，如何真正的找到这个低维平面

4 . Principal Component Analysis Algorithm

这节介绍PCA的实现过程。并应用PCA进行数据降维。

在应用之前，要有一个数据预处理过程。

一般要进行均值归一化(mean normalization)

当然，也可以进特征缩放(feature scaling)

(简单对之前的东西复习一下)

下面开始介绍算法：

先回顾一下大致实现过程：

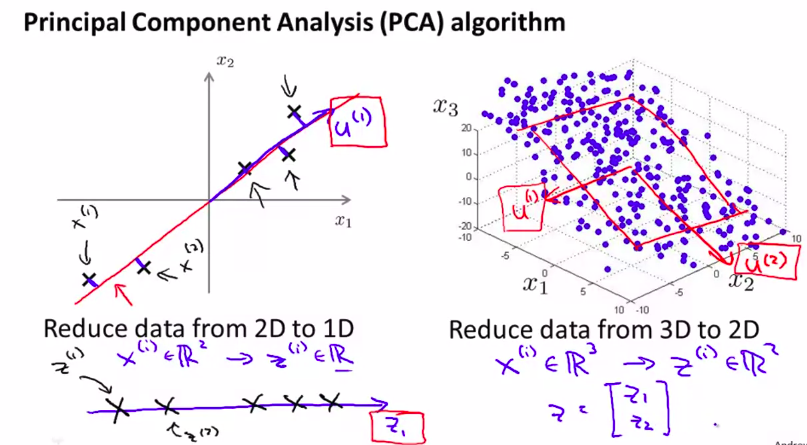
接下来，就是要计算：

协方差矩阵(covariance matrix)

本节课用字母 \(\Sigma\) 来表示

然后，我们需要做的就是计算出这个协方差矩阵的特征向量

这一步可以用命令：

[U,S,V] = svd(Sigma)

来实现。这个，命令叫做：

svd(singular value decomposition)

奇异值分解

如图：

当然，eig函数也是一样的效果，老师比较喜欢用svd

这是因为协方差矩阵总是满足一个数学性质：

称为：对称正定(symmetric positive definite)

当然，只要记住这个命令即可。数学细节可以不用在意don’t care it

let’s go on:

我们知道，这个协方差矩阵是一个n×n的矩阵

然后，svd函数输出三个矩阵

分别是U，S，V。

我们真正需要的是U。当然也是n×n矩阵》

然后，得到U后，如果我们想将数据的维度从n降低到k的话，我们只需要提取前k列的向量，即我们就得到了u(1)到u(k),也就是我们用来投影数据的k个方向。

最后，我们需要找到一个表达式来用，高维数据转化为低维数据

然后计算方法是：

然后我们就得到了k维数据的z

具体操作：

这就是PCA算法

当然，数学证明可以在bing上查到：

纯数学解释：https://zhuanlan.zhihu.com/p/26951643

带图详解过程：https://blog.csdn.net/aiaiai010101/article/details/72744713

5. Reconstruction from Compressed Representation

如何还原压缩过的数据？

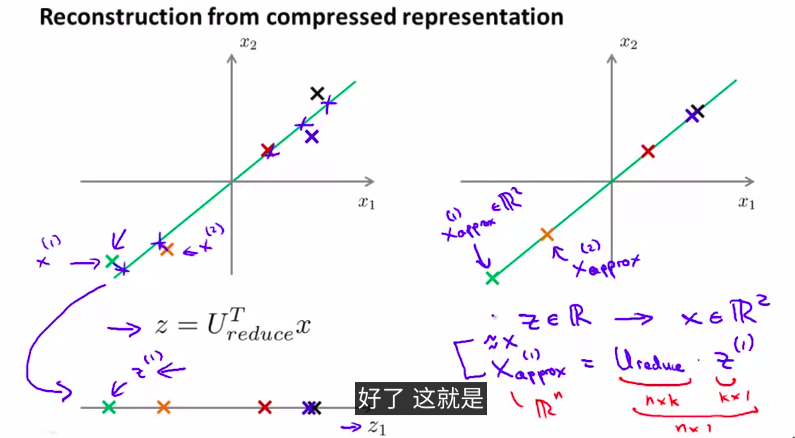
当然，数据肯定会有些许误差

6. Choosing the Number of Principal Components

如何选择k？k也被称为主成分的数量

PCA所要做的是尽量最小化 平均平方映射误差(Average Squared Projection Error)

还有就是数据的总变量：

所以，选择k的原则就是：

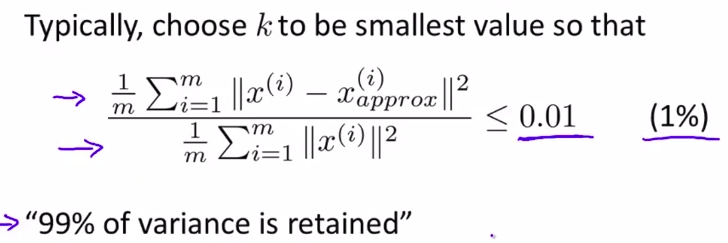
所以很多人并不是要选择k，而是要求k使这个有99%的差异性被保留。

所以0.01是很常用的，还有一个是0.05，或者0.10

都是很常用的取值范围

这样开始：（懒得打字了）

不停的试k！！！简单粗暴，效率低下！

当然，还有一种可以使方法变得简单的方法

这个方法十分高效，你只要调用一次svd，然后就能算出S。然后，你只要不断加 k 就可以了！！

所以，当你手动选择k的时候，说明k‘的性能也可以用这个东西来描述：

7. Advice for Applying PCA

例如，图片有很多维的向量，所以要压缩

降维对我们的算法很有帮助。低维数据能让算法运行得更快！更有效率，而且其精度也不会影响太多。

应用：

不好的应用：

避免过度拟合：

怎么可能这么想当然！

因为PCA在作用的时候，是没有label的，所以说，在压缩的过程中，会丢失一些数据和信息！

我们一般用正则化来做这件事

PCA的误用：

设计一个机器学习算法的时候，不要一开始就用PCA，最好先用原始数据来算一遍。