Python数据科学手册-机器学习: 流形学习

PCA对非线性的数据集处理效果不太好。

另一种方法 流形学习 manifold learning

是一种无监督评估器，试图将一个低维度流形嵌入到一个高纬度 空间来描述数据集 。

类似 一张纸 （二维） 卷起 弄皱 （三维）。二维流形 嵌入到一个三维空间， 就不再是线性的了。

流形方法技巧：

• 多维标度法 multidimensional scaling MSD
• 局部线性嵌入法 locally linear embedding LLE
• 保距映射法 isometric mapping Isomap

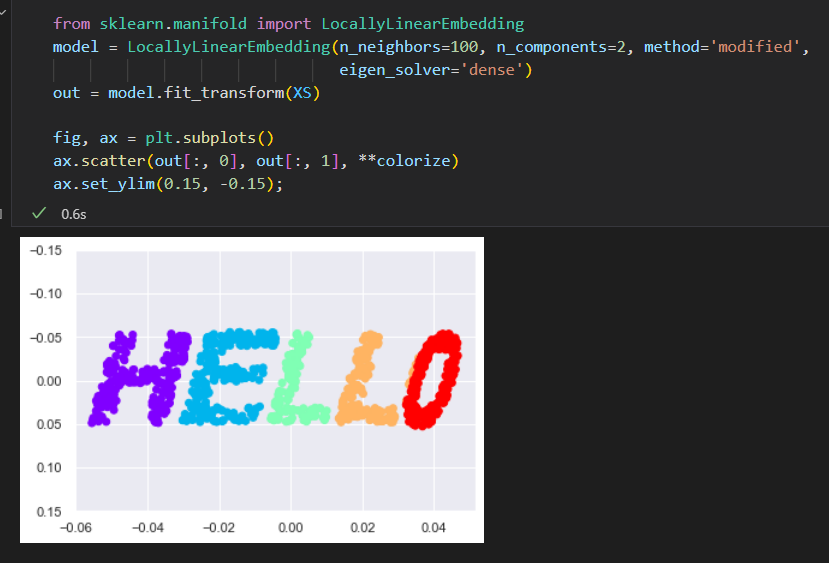
流形学习：HELLO

生成一些二维数据来定义一个流形。

创建一组数据，构成单词hello的形状





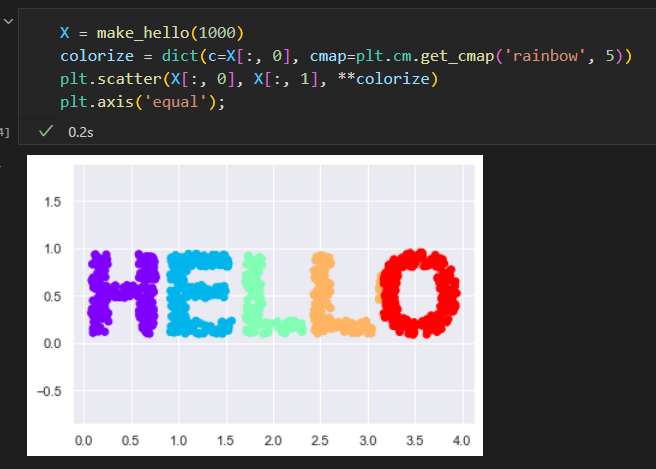
输出图像包含了很多二维的点。

多维标度法

x和 y 的值并不是数据间关系 的必要基础特征， 真正的基础特征是每个点与数据 集中其他 点 的距离。

表示这种关系的常用方法是 关系 距离 矩阵： 对于N个点。构建一个NxN的矩阵， 元素（i,j)是 点 i和点j之间的距离。

使用pairwise_distances函数计算原始数据的关系矩阵





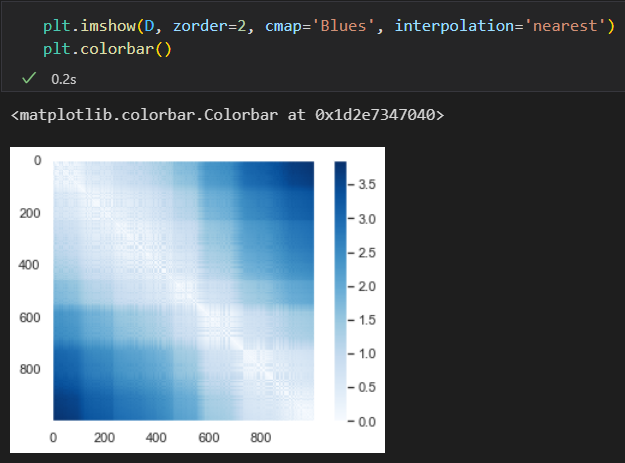
这个距离矩阵给出了一个数据集内部关系的表现形式，这种形式与数据集的旋转和投影无关系，但距离矩阵的可视化效果显得不够直观。

虽然从（x,y）坐标计算这个距离矩阵很简单，但是从距离矩阵转回到（x,y）却很困难。

这就是多维标度发可以解决的问题：他可以将一个数据集的距离矩阵还原成一个D维坐标来表示数据集。

看多维度表法是如何还原距离矩阵的，仅仅依靠描述数据点间关系的NXN距离矩阵，就可以还原出一种可行的二维坐标。

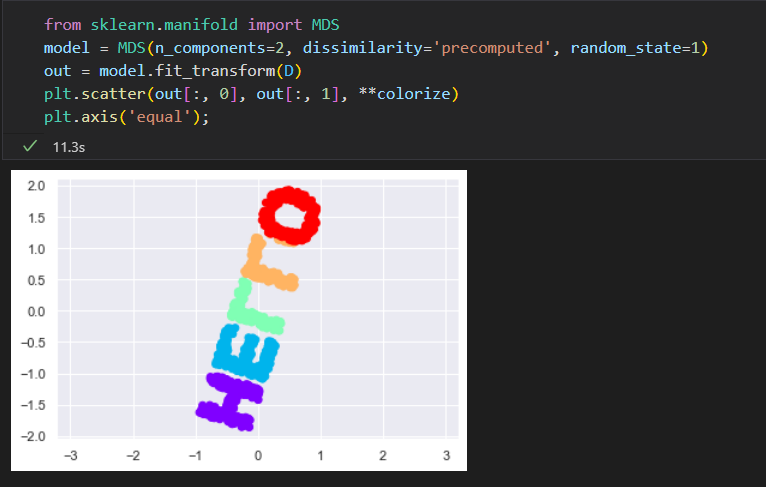
将MDS用于流形学习

既然距离矩阵可以冲数据的任意维度进行计算。 那么这种方法绝对非常实用，

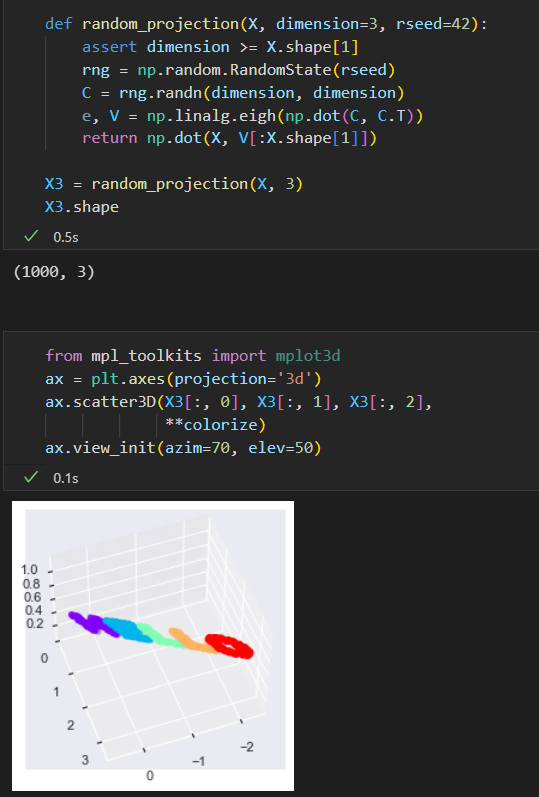
既然可以在一个二维平面中简单的旋转数据，那么也可以用一下函数将其投影到三维孔家。



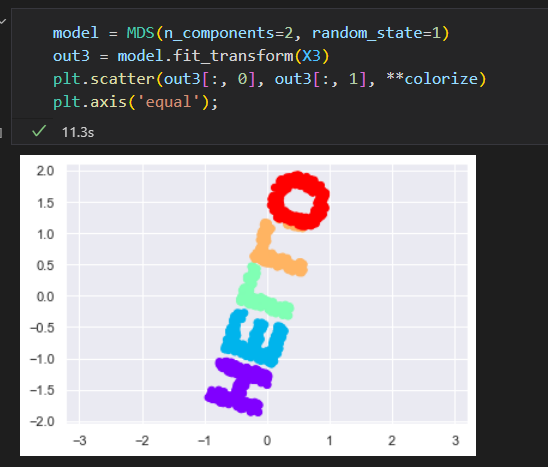
可以通过MDS评估器输入这个三维数据，计算距离急症，然后得出距离矩阵的最优二维嵌入结果。结果还原了原始数据的形状



以上就是使用流形学习评估器希望 达成的目标： 给的一个高维嵌入数据，寻找数据的一个低维表示。并保留数据间的特定关系。

在MDS示例中。保留的数据是每对数据点之间的距离。

非线性嵌入：当MDS失败是

当嵌入为非线性是，集超越简单的操作集合时，MDS算法就会失效。

将输入数据在三维空间中扭曲成 S形状的示例



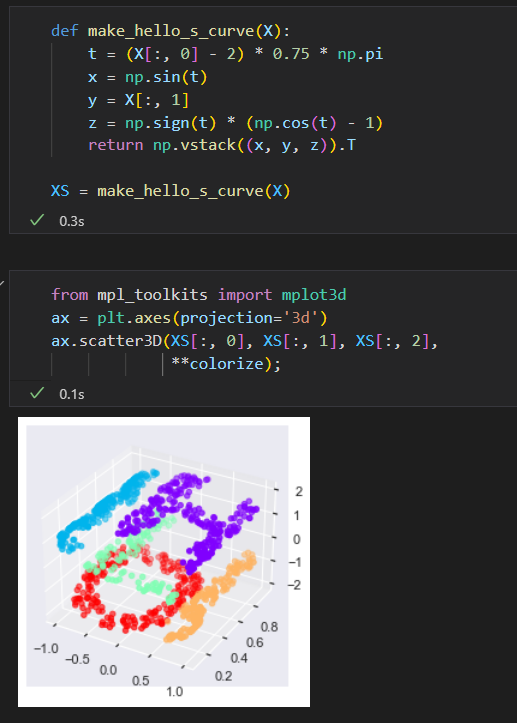
尝试用MDS算法来处理这个数据，就无法展示数据非线性嵌入的特征。进而导致我们丢失了这个嵌入式流形的内部基本关系特性。

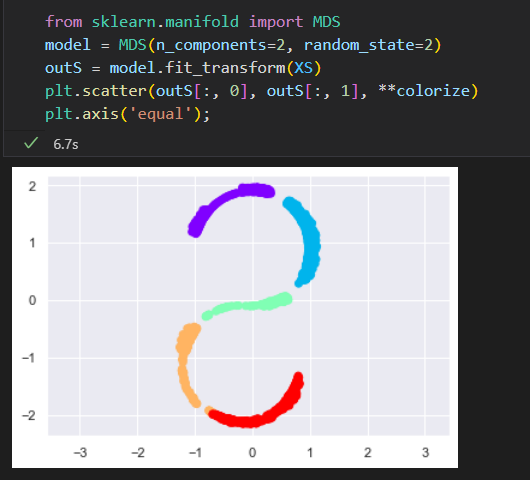
非线性流形： 局部线性嵌入

MDS算法构建嵌入式，总是期望保留相聚很远的数据点之间的距离。如果修改算法，只保留比较接近的点之间的距离。嵌入的结果可能会与我们的期望更接近。



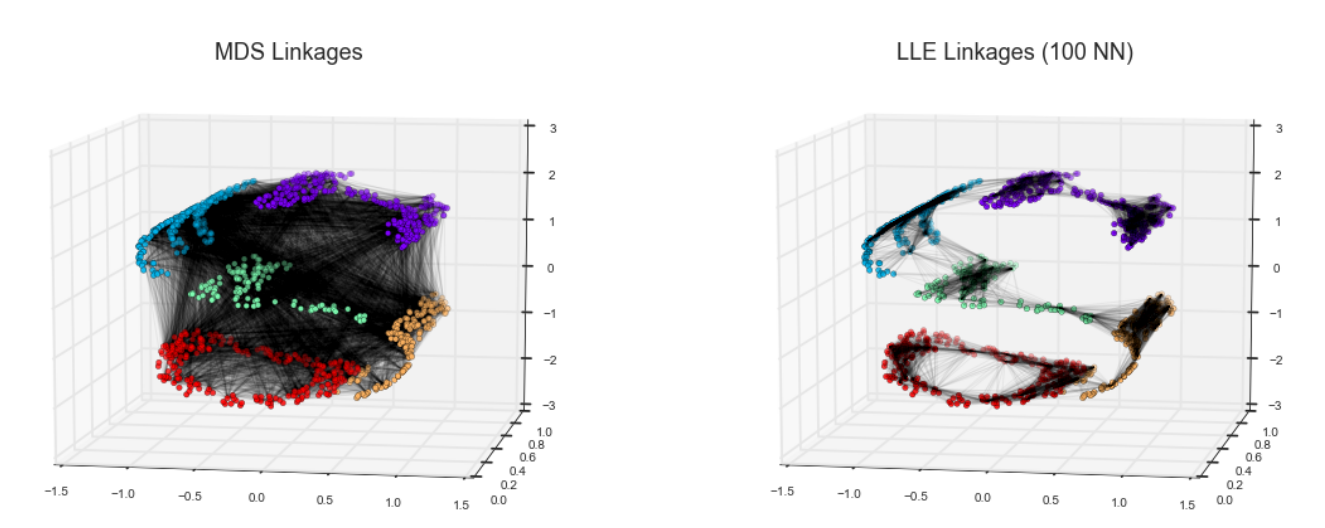
其中每一条细小的线都表示在嵌入式会保留的距离。不保留所有的距离。仅保留邻节点 间的距离。 每个点最近的100个邻节点。