POJ 3449 Geometric Shapes (求正方形的另外两点)

Geometric Shapes

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 1470		Accepted: 622

Description

While creating a customer logo, ACM uses graphical utilities to draw a picture that can later be cut into special fluorescent materials. To ensure proper processing, the shapes in the picture cannot intersect. However, some logos contain such intersecting shapes. It is necessary to detect them and decide how to change the picture.

Given a set of geometric shapes, you are to determine all of their intersections. Only outlines are considered, if a shape is completely inside another one, it is not counted as an intersection.

Input

Input contains several pictures. Each picture describes at most 26 shapes, each specified on a separate line. The line begins with an uppercase letter that uniquely identifies the shape inside the corresponding picture. Then there is a kind of the shape and two or more points, everything separated by at least one space. Possible shape kinds are:

• square: Followed by two distinct points giving the opposite corners of the square.
• rectangle: Three points are given, there will always be a right angle between the lines connecting the first point with the second and the second with the third.
• line: Specifies a line segment, two distinct end points are given.
• triangle: Three points are given, they are guaranteed not to be co-linear.
• polygon: Followed by an integer number N (3 ≤ N ≤ 20) and N points specifying vertices of the polygon in either clockwise or anti-clockwise order. The polygon will never intersect itself and its sides will have non-zero length.

All points are always given as two integer coordinates X and Y separated with a comma and enclosed in parentheses. You may assume that |X|, |Y | ≤ 10000.

The picture description is terminated by a line containing a single dash (“-”). After the last picture, there is a line with one dot (“.”).

Output

For each picture, output one line for each of the shapes, sorted alphabetically by its identifier (X). The line must be one of the following:

• “X has no intersections”, if X does not intersect with any other shapes.
• “X intersects with A”, if X intersects with exactly 1 other shape.
• “X intersects with A and B”, if X intersects with exactly 2 other shapes.
• “X intersects with A, B, . . ., and Z”, if X intersects with more than 2 other shapes.

Please note that there is an additional comma for more than two intersections. A, B, etc. are all intersecting shapes, sorted alphabetically.

Print one empty line after each picture, including the last one.

Sample Input

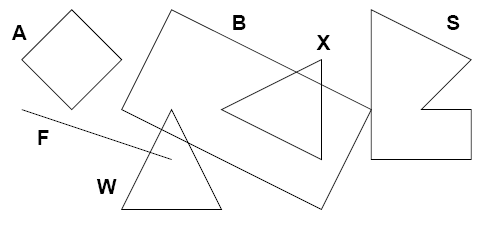
A square (1,2) (3,2)
F line (1,3) (4,4)
W triangle (3,5) (5,5) (4,3)
X triangle (7,2) (7,4) (5,3)
S polygon 6 (9,3) (10,3) (10,4) (8,4) (8,1) (10,2)
B rectangle (3,3) (7,5) (8,3)
-
B square (1,1) (2,2)
A square (3,3) (4,4)
-
.

Sample Output

A has no intersections
B intersects with S, W, and X
F intersects with W
S intersects with B
W intersects with B and F
X intersects with B
 
A has no intersections
B has no intersections

Source

CTU Open 2007

这个题目有个小的知识点就是知道正方形的对角线上的两个点坐标，求出其他两个点，我刚开始是用向量旋转做的，后来觉得一定还有其他的办法，因为正方形比较特殊，后来去网上搜到了可以直接用对角线上的坐标(x0,y0),(x2,y2)来求，对应关系如下：

x1 + x3 = x0 + x2;

x1 - x3 = y2 - y0;

y1 + y3 = y0 + y2;

y3 - y1 = x2 - x0;

求得另一对不相邻的顶点(x1,y1),(x3,y3)。

x1 = (x0 + x2 + y2 - y0) / 2

x3 = (x0 + x2 + y0 - y2) / 2

y1 = (y0 + y2 + x0 - x2) / 2

y3 = (y0 + y2 - x0 + x2) / 2

这样的话其他就没有难点了，就是遍历每个图形，看是否与其他的相交，如果不知道向量如何旋转的，请看http://www.cnblogs.com/Howe-Young/p/4466975.html

/*************************************************************************
    > File Name:            poj_3449.cpp
    > Author:               Howe_Young
    > Mail:                 1013410795@qq.com
    > Created Time:         2015年05月01日 星期五 18时38分39秒
 ************************************************************************/
 
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
 
using namespace std;
const int maxn = ;
struct point{
    double x, y;
};
struct shape{
    char id;
    char name[];
    point edge[];
    char info[maxn];
    int index, num;
};
shape s[maxn];
int n, i;
char ch;
void input()
{
        s[i].id = ch;
        s[i].index = ;
        scanf("%s", s[i].name);
        if (strcmp(s[i].name, "square") == )
        {
            scanf(" (%lf, %lf) (%lf, %lf)", &s[i].edge[].x, &s[i].edge[].y, &s[i].edge[].x, &s[i].edge[].y);
            s[i].edge[].x = (s[i].edge[].x + s[i].edge[].x + s[i].edge[].y - s[i].edge[].y) / ;
            s[i].edge[].y = (s[i].edge[].y + s[i].edge[].y - s[i].edge[].x + s[i].edge[].x) / ;
            s[i].edge[].x = (s[i].edge[].x + s[i].edge[].x - s[i].edge[].y + s[i].edge[].y ) / ;
            s[i].edge[].y = (s[i].edge[].y + s[i].edge[].y + s[i].edge[].x - s[i].edge[].x) / ;
            s[i].num = ;
            return;
        }
        else if (strcmp(s[i].name, "rectangle") == )
        {
            scanf(" (%lf,%lf) (%lf, %lf) (%lf, %lf)", &s[i].edge[].x, &s[i].edge[].y, &s[i].edge[].x, &s[i].edge[].y, &s[i].edge[].x, &s[i].edge[].y);
            s[i].edge[].x = s[i].edge[].x + s[i].edge[].x - s[i].edge[].x;
            s[i].edge[].y = s[i].edge[].y + s[i].edge[].y - s[i].edge[].y;
            s[i].num = ;
            return;
        }
        else if (strcmp(s[i].name, "line") == )
        {
            scanf(" (%lf, %lf) (%lf, %lf)", &s[i].edge[].x, &s[i].edge[].y, &s[i].edge[].x, &s[i].edge[].y);
            s[i].num = ;
            return;
        }
        else if(strcmp(s[i].name, "triangle") == )
        {
            scanf(" (%lf, %lf) (%lf, %lf) (%lf, %lf)", &s[i].edge[].x, &s[i].edge[].y, &s[i].edge[].x, &s[i].edge[].y, &s[i].edge[].x, &s[i].edge[].y);
            s[i].num = ;
            return;
        }
        else
        {
            int k;
            scanf("%d", &k);
            for (int j = ; j < k; j++)
                scanf(" (%lf, %lf)", &s[i].edge[j].x, &s[i].edge[j].y);
            s[i].num = k;
            return;
        }
 
}
double x_multi(point p1, point p2, point p3)
{
    return (p3.x - p1.x) * (p2.y - p1.y) - (p2.x - p1.x) * (p3.y - p1.y);
}
bool on_segment(point p1, point p2, point p3)
{
    double minx, miny, maxx, maxy;
    if (p1.x > p2.x)
    {
        minx = p2.x;
        maxx = p1.x;
    }
    else
    {
        minx = p1.x;
        maxx = p2.x;
    }
    if (p1.y > p2.y)
    {
        miny = p2.y;
        maxy = p1.y;
    }
    else
    {
        maxy = p2.y;
        miny = p1.y;
    }
    return (p3.x >= minx && p3.x <= maxx && p3.y >= miny && p3.y <= maxy);
}
bool segment_intersect(point p1, point p2, point p3, point p4)
{
    double d1 = x_multi(p1, p2, p3);
    double d2 = x_multi(p1, p2, p4);
    double d3 = x_multi(p3, p4, p1);
    double d4 = x_multi(p3, p4, p2);
    if (d1 * d2 <  && d3 * d4 < )
        return true;
    if (d1 ==  && on_segment(p1, p2, p3))
        return true;
    if (d2 ==  && on_segment(p1, p2, p4))
        return true;
    if (d3 ==  && on_segment(p3, p4, p1))
        return true;
    if (d4 ==  && on_segment(p3, p4, p2))
        return true;
    return false;
}
bool intersected(shape a, shape b)
{
    for (int p = ; p <= a.num; p++)
    {
        for (int q = ; q <= b.num; q++)
        {
            if (segment_intersect(a.edge[p - ], a.edge[p % a.num], b.edge[q - ], b.edge[q % b.num]))
            {
                return true;
            }
        }
    }
    return false;
}
bool cmp1(const shape a, const shape b)
{
    return a.id < b.id;
}
bool cmp2(const char a, const char b)
{
    return a < b;
}
void output(shape a)
{
    if (a.index == )
    {
        printf("%c has no intersections\n", a.id);
        return;
    }
    if (a.index == )
    {
        printf("%c intersects with %c\n", a.id, a.info[]);
        return;
    }
    if (a.index == )
    {
        printf("%c intersects with %c and %c\n", a.id, a.info[], a.info[]);
        return;
    }
    printf("%c intersects with %c, ", a.id, a.info[]);
    for (int t = ; t < a.index - ; t++)
        printf("%c, ", a.info[t]);
    printf("and %c\n", a.info[a.index - ]);
 
}
int main()
{
    while (cin >> ch && ch != '.')
    {
        memset(s, , sizeof(s));
        i = ;
        if (ch == '-')
            continue;
        input();
        while (cin >> ch)
        {
            i++;
            if (ch == '-')
                break;
            input();
        }
        n = i;
        for (int t = ; t < n; t++)
        {
            for (int j = t + ; j < n; j++)
            {
                if (intersected(s[t], s[j]))
                {
                    s[t].info[s[t].index++] = s[j].id;
                    s[j].info[s[j].index++] = s[t].id;
                }
            }
        }
        sort(s, s + n, cmp1);
        for (int t = ; t < n; t++)
        {
            sort(s[t].info, s[t].info + s[t].index, cmp2);
            output(s[t]);
        }
        puts("");
    }
    return ;
}