交替方向乘子法（ADMM）

参考1

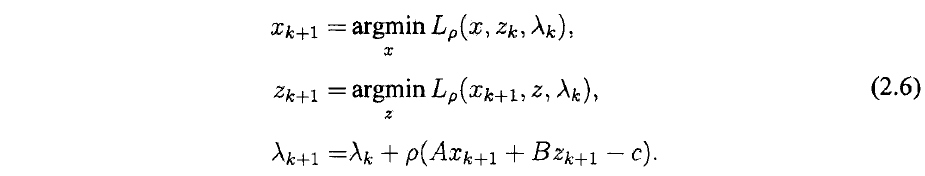
参考2

经典的ADMM算法适用于求解如下2-block的凸优化问题（ $p^*$ 是最优值，令 $x^*,z^*$ 表示一组最优解）：

$\begin{align} p^* = \min ~ & f(x)+g(z)\\ \text{s.t. } & Ax+Bz=c. \end{align}$

Block指我们可以将决策域分块，分成两组变量， $x\in \mathbb{R}^n,z\in \mathbb{R}^m.$ 这里面 $A\in \mathbb{R}^{p\times n},B\in \mathbb{R}^{p\times m},c\in \mathbb{R}^p.$ $f:\mathbb{R}^n\rightarrow \mathbb{R},g:\mathbb{R}^m\rightarrow \mathbb{R}$ 都是凸的。分成2-block是因为3-block及以上的问题性质会差一点，分析起来不太好说清楚（虽然实际当中基本上几个block都可以用，一般都会收敛...）。

那么我们这里就可以写出这个凸优化问题的增广拉格朗日函数（augmented Lagrangian function）：

$L_{\rho}(x,z,y)=f(x)+g(z)+y^T(Ax+Bz-c)+(\rho/2)\|Ax+Bz-c\|_2^2.$

注意到这个增广的意思就是在原来的拉格朗日函数后面加了个平方的正则项（系数 $\rho/2$ ），这个主要是为了不需要 $f$ 一定要是严格凸（strictly convex）/值域有限（只要是一般的凸函数就行了）然后也能保证收敛性。然后我们对 $L_\rho$ 用dual ascent（对偶上升法），或者也就是拉格朗日乘子法就知道可以有这样一个算法形式：

$\begin{align} (x^{k+1},z^{k+1}):=~ & \arg\min_{x,z} L_{\rho}(x,z,y^k)\\ y^{k+1}:= ~ & y^k+\rho(Ax^{k+1}+Bz^{k+1}-c). \end{align}$

其实dual ascent原理非常简单，本质上来说就是primal variable迭代方向取拉格朗日函数对primal variable的次微分，dual variable迭代方向取拉格朗日函数对dual variable的次微分（这里的话就是 $\frac{\partial L_{\rho}}{\partial y}$ ）。这也是所谓拉格朗日乘子法的一般思路（method of multipliers）。当然这边还有一些细节，比如对偶变量迭代步长选了 $\rho$ 。所以如果你想从基础打起的话，可以从比如S. Boyd and L. Vandenberghe的凸优化书第五章看起。

那么ADMM，也就是所谓“交替方向”的乘子法就是在原基础上（ $x,z$ 一起迭代）改成 $x,z$ 单独交替迭代（如果有更多block也是类似）。即，我们的ADMM算法为

$\begin{align} x^{k+1}:=~ & \arg\min_{x} L_{\rho}(x,z^k,y^k)\\ z^{k+1}:=~ & \arg\min_{z} L_{\rho}(x^{k+1},z,y^k)\\ y^{k+1}:= ~ & y^k+\rho(Ax^{k+1}+Bz^{k+1}-c). \end{align}$

本节最后，我们指出ADMM算法形式的另一种等价形式。如果定义所谓的残差（residual）为 $r^k:=Ax^k+Bz^k-c$ ，那么注意到再定义 $u^k:=(1/\rho)y^k$ 作为所谓scaled dual variable，我们有 $(y^k)^Tr^k+(\rho/2)\|r^k\|_2^2=(\rho/2)\|r^k+u^k\|_2^2-(\rho/2)\|u^k\|_2^2.$ 即我们可以改写ADMM算法形式为

$\begin{align} x^{k+1}:=~ & \arg\min_{x} \left\{ f(x)+(\rho/2)\|Ax+Bz^k-c+u^k\|_2^2 \right\}\\ z^{k+1}:=~ & \arg\min_{z} \left\{ g(z)+(\rho/2)\|Ax^{k+1}+Bz-c+u^k\|_2^2 \right\}\\ u^{k+1}:= ~ & u^k+Ax^{k+1}+Bz^{k+1}-c. \end{align}$

嗯这个形式就比前面那个更简洁些，我们一般叫前一种形式为ADMM的unscaled形式，而这种就自然是scaled形式了。很多ADMM分析都是基于这个scaled形式的。

参考文献

ADMM ：http://web.stanford.edu/~boyd/admm.html

许浩锋. 基于交替方向乘子法的分布式在线学习算法[D]. 中国科学技术大学, 2015.

覃含章：https://www.zhihu.com/question/309568920/answer/580226096

用ADMM实现统计学习问题的分布式计算 · MullOver ：http://shijun.wang/2016/01/19/admm-for-distributed-statistical-learning/

《凸优化》中文版PDF+英文版PDF+习题题解：https://pan.baidu.com/s/1oRGp4_LfDVLo86r79pnXvg