树链剖分详解（洛谷模板 P3384）

洛谷·[模板]树链剖分

写在前面

首先，在学树链剖分之前最好先把 LCA、树形DP、DFS序 这三个知识点学了

emm还有必备的 链式前向星、线段树 也要先学了。

如果这三个知识点没掌握好的话，树链剖分难以理解也是当然的。

---

树链剖分

树链剖分 就是对一棵树分成几条链，把树形变为线性，减少处理难度

需要处理的问题：

• 将树从x到y结点最短路径上所有节点的值都加上z
• 求树从x到y结点最短路径上所有节点的值之和
• 将以x为根节点的子树内所有节点值都加上z
• 求以x为根节点的子树内所有节点值之和

目录：

• 概念

• dfs1()

• dfs2()

• 处理问题

• 对剖过后的树建线段树

概念

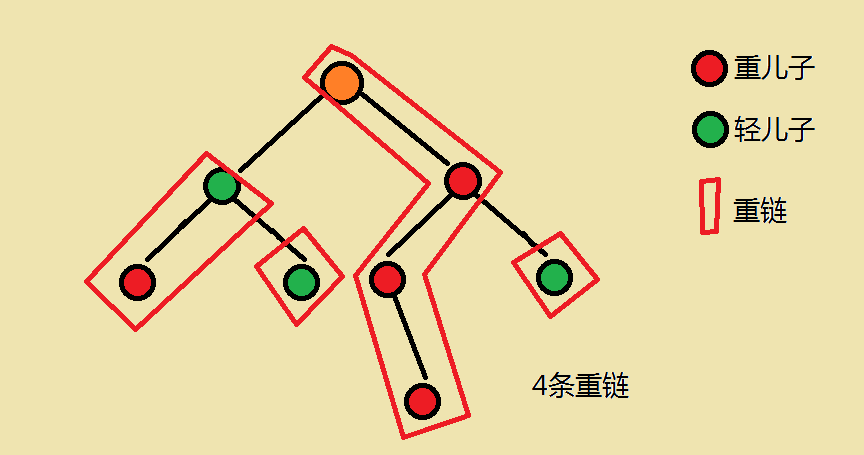
• 重儿子：对于每一个非叶子节点，它的儿子中 以那个儿子为根的子树节点数最大的儿子 为该节点的重儿子 (Ps: 感谢@shzr大佬指出我此句话的表达不严谨qwq, 已修改)
• 轻儿子：对于每一个非叶子节点，它的儿子中 非重儿子 的剩下所有儿子即为轻儿子
• 叶子节点没有重儿子也没有轻儿子（因为它没有儿子。。）
• 重边：一个父亲连接他的重儿子的边称为重边 //原写法：连接任意两个重儿子的边叫做重边
• 轻边：剩下的即为轻边
• 重链：相邻重边连起来的 连接一条重儿子 的链叫重链
  • 对于叶子节点，若其为轻儿子，则有一条以自己为起点的长度为1的链
  • 每一条重链以轻儿子为起点

dfs1()

这个dfs要处理几件事情：

• 标记每个点的深度dep[]
• 标记每个点的父亲fa[]
• 标记每个非叶子节点的子树大小(含它自己)
• 标记每个非叶子节点的重儿子编号son[]

inline void dfs1(int x,int f,int deep){//x当前节点，f父亲，deep深度
	dep[x]=deep;//标记每个点的深度
	fa[x]=f;//标记每个点的父亲
	siz[x]=1;//标记每个非叶子节点的子树大小
	int maxson=-1;//记录重儿子的儿子数
	for(Rint i=beg[x];i;i=nex[i]){
		int y=to[i];
		if(y==f)continue;//若为父亲则continue
		dfs1(y,x,deep+1);//dfs其儿子
		siz[x]+=siz[y];//把它的儿子数加到它身上
		if(siz[y]>maxson)son[x]=y,maxson=siz[y];//标记每个非叶子节点的重儿子编号
	}
}//变量解释见最下面

dfs2()

这个dfs2也要预处理几件事情

• 标记每个点的新编号
• 赋值每个点的初始值到新编号上
• 处理每个点所在链的顶端
• 处理每条链

顺序：先处理重儿子再处理轻儿子，理由后面说

inline void dfs2(int x,int topf){//x当前节点，topf当前链的最顶端的节点
	id[x]=++cnt;//标记每个点的新编号
	wt[cnt]=w[x];//把每个点的初始值赋到新编号上来
	top[x]=topf;//这个点所在链的顶端
	if(!son[x])return;//如果没有儿子则返回
	dfs2(son[x],topf);//按先处理重儿子，再处理轻儿子的顺序递归处理
	for(Rint i=beg[x];i;i=nex[i]){
		int y=to[i];
		if(y==fa[x]||y==son[x])continue;
		dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链
	}
}//变量解释见最下面

处理问题

Attention 重要的来了！！！

前面说到dfs2的顺序是先处理重儿子再处理轻儿子

我们来模拟一下：

• 因为顺序是先重再轻，所以每一条重链的新编号是连续的
• 因为是dfs，所以每一个子树的新编号也是连续的

现在回顾一下我们要处理的问题

• 处理任意两点间路径上的点权和
• 处理一点及其子树的点权和
• 修改任意两点间路径上的点权
• 修改一点及其子树的点权

1、当我们要处理任意两点间路径时：

设所在链顶端的深度更深的那个点为x点

• ans加上x点到x所在链顶端 这一段区间的点权和
• 把x跳到x所在链顶端的那个点的上面一个点

不停执行这两个步骤，直到两个点处于一条链上，这时再加上此时两个点的区间和即可

这时我们注意到，我们所要处理的所有区间均为连续编号(新编号)，于是想到线段树，用线段树处理连续编号区间和

每次查询时间复杂度为\(O( \log^2n)\)

inline int qRange(int x,int y){
	int ans=0;
	while(top[x]!=top[y]){//当两个点不在同一条链上
		if(dep[top[x]]<dep[top[y]])swap(x,y);//把x点改为所在链顶端的深度更深的那个点
		res=0;
		query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
		ans+=res;
		ans%=mod;//按题意取模
		x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
	}
	//直到两个点处于一条链上
	if(dep[x]>dep[y])swap(x,y);//把x点深度更深的那个点
	res=0;
	query(1,1,n,id[x],id[y]);//这时再加上此时两个点的区间和即可
	ans+=res;
	return ans%mod;
}//变量解释见最下面

2、处理一点及其子树的点权和：

想到记录了每个非叶子节点的子树大小(含它自己)，并且每个子树的新编号都是连续的

于是直接线段树区间查询即可

时间复杂度为\(O( \log n)\)

inline int qSon(int x){
	res=0;
	query(1,1,n,id[x],id[x]+siz[x]-1);//子树区间右端点为id[x]+siz[x]-1
	return res;
}

当然，区间修改就和区间查询一样的啦~~

inline void updRange(int x,int y,int k){
	k%=mod;
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		update(1,1,n,id[top[x]],id[x],k);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	update(1,1,n,id[x],id[y],k);
}

inline void updSon(int x,int k){
	update(1,1,n,id[x],id[x]+siz[x]-1,k);
}//变量解释见最下面

建树

既然前面说到要用线段树，那么按题意建树就可以啦！

不过，建树这一步当然是在处理问题之前哦~

AC代码：

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#define Rint register int
#define mem(a,b) memset(a,(b),sizeof(a))
#define Temp template<typename T>
using namespace std;
typedef long long LL;
Temp inline void read(T &x){
    x=0;T w=1,ch=getchar();
    while(!isdigit(ch)&&ch!='-')ch=getchar();
    if(ch=='-')w=-1,ch=getchar();
    while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
    x=x*w;
}

#define mid ((l+r)>>1)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define len (r-l+1)

const int maxn=200000+10;
int n,m,r,mod;
//见题意
int e,beg[maxn],nex[maxn],to[maxn],w[maxn],wt[maxn];
//链式前向星数组，w[]、wt[]初始点权数组
int a[maxn<<2],laz[maxn<<2];
//线段树数组、lazy操作
int son[maxn],id[maxn],fa[maxn],cnt,dep[maxn],siz[maxn],top[maxn];
//son[]重儿子编号,id[]新编号,fa[]父亲节点,cnt dfs_clock/dfs序,dep[]深度,siz[]子树大小,top[]当前链顶端节点
int res=0;
//查询答案 

inline void add(int x,int y){//链式前向星加边
    to[++e]=y;
    nex[e]=beg[x];
    beg[x]=e;
}
//-------------------------------------- 以下为线段树
inline void pushdown(int rt,int lenn){
	laz[rt<<1]+=laz[rt];
	laz[rt<<1|1]+=laz[rt];
    a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
    a[rt<<1|1]+=laz[rt]*(lenn>>1);
    a[rt<<1]%=mod;
    a[rt<<1|1]%=mod;
    laz[rt]=0;
}

inline void build(int rt,int l,int r){
    if(l==r){
        a[rt]=wt[l];
        if(a[rt]>mod)a[rt]%=mod;
        return;
    }
    build(lson);
    build(rson);
    a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
}

inline void query(int rt,int l,int r,int L,int R){
	if(L<=l&&r<=R){res+=a[rt];res%=mod;return;}
	else{
		if(laz[rt])pushdown(rt,len);
		if(L<=mid)query(lson,L,R);
		if(R>mid)query(rson,L,R);
	}
}

inline void update(int rt,int l,int r,int L,int R,int k){
    if(L<=l&&r<=R){
		laz[rt]+=k;
		a[rt]+=k*len;
	}
	else{
		if(laz[rt])pushdown(rt,len);
		if(L<=mid)update(lson,L,R,k);
		if(R>mid)update(rson,L,R,k);
		a[rt]=(a[rt<<1]+a[rt<<1|1])%mod;
	}
}
//---------------------------------以上为线段树
inline int qRange(int x,int y){
	int ans=0;
	while(top[x]!=top[y]){//当两个点不在同一条链上
		if(dep[top[x]]<dep[top[y]])swap(x,y);//把x点改为所在链顶端的深度更深的那个点
		res=0;
		query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
		ans+=res;
		ans%=mod;//按题意取模
		x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
	}
	//直到两个点处于一条链上
	if(dep[x]>dep[y])swap(x,y);//把x点深度更深的那个点
	res=0;
	query(1,1,n,id[x],id[y]);//这时再加上此时两个点的区间和即可
	ans+=res;
	return ans%mod;
}

inline void updRange(int x,int y,int k){//同上
	k%=mod;
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		update(1,1,n,id[top[x]],id[x],k);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	update(1,1,n,id[x],id[y],k);
}

inline int qSon(int x){
	res=0;
	query(1,1,n,id[x],id[x]+siz[x]-1);//子树区间右端点为id[x]+siz[x]-1
	return res;
}

inline void updSon(int x,int k){//同上
	update(1,1,n,id[x],id[x]+siz[x]-1,k);
}

inline void dfs1(int x,int f,int deep){//x当前节点，f父亲，deep深度
	dep[x]=deep;//标记每个点的深度
	fa[x]=f;//标记每个点的父亲
	siz[x]=1;//标记每个非叶子节点的子树大小
	int maxson=-1;//记录重儿子的儿子数
	for(Rint i=beg[x];i;i=nex[i]){
		int y=to[i];
		if(y==f)continue;//若为父亲则continue
		dfs1(y,x,deep+1);//dfs其儿子
		siz[x]+=siz[y];//把它的儿子数加到它身上
		if(siz[y]>maxson)son[x]=y,maxson=siz[y];//标记每个非叶子节点的重儿子编号
	}
}

inline void dfs2(int x,int topf){//x当前节点，topf当前链的最顶端的节点
	id[x]=++cnt;//标记每个点的新编号
	wt[cnt]=w[x];//把每个点的初始值赋到新编号上来
	top[x]=topf;//这个点所在链的顶端
	if(!son[x])return;//如果没有儿子则返回
	dfs2(son[x],topf);//按先处理重儿子，再处理轻儿子的顺序递归处理
	for(Rint i=beg[x];i;i=nex[i]){
		int y=to[i];
		if(y==fa[x]||y==son[x])continue;
		dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链
	}
}

int main(){
    read(n);read(m);read(r);read(mod);
    for(Rint i=1;i<=n;i++)read(w[i]);
    for(Rint i=1;i<n;i++){
        int a,b;
        read(a);read(b);
        add(a,b);add(b,a);
    }
    dfs1(r,0,1);
    dfs2(r,r);
    build(1,1,n);
	while(m--){
        int k,x,y,z;
        read(k);
        if(k==1){
            read(x);read(y);read(z);
            updRange(x,y,z);
        }
        else if(k==2){
            read(x);read(y);
            printf("%d\n",qRange(x,y));
        }
        else if(k==3){
            read(x);read(y);
            updSon(x,y);
        }
        else{
            read(x);
            printf("%d\n",qSon(x));
    	}
    }
}