HDU-problem-1002-人类史上最大最好的希望事件-矩阵快速幂

Problem Description

作为CNCS的半壁江山，狗哥常常在宇宙中心邵阳眺望黄浦江，夜晚的星空总是迷人，有时候还能见到彗星滑落。

狗哥是幸运的，他在两秒钟内看到了十七颗彗星划过天际，作为打ACM的学者，自然不会有「稳定-1」情况。他开始研究彗星运动的轨迹，发现他们都遵照斐波那契螺旋线在运动着。

尤里卡！狗哥觉得这就是找寻「生命，宇宙和一切的终极答案」的精要所在，但是怎么表示呢？狗哥觉得求取斐波那契螺旋线经过的一个个方格的面积之和就是公式的表现。

例如下图，螺旋线每划过一个方格，都转过了四分之一圈。如果我们以四分之一圈为单位，那么我们用类似带分数的形式表示螺旋线转动的起点和终点。例如，0+0
到 0 + 1 意即从第一个方格转到第二个方格，划过了前两个方格，他们的面积之和为2（1+1）。同理，0+0 到 1+0
划过了前五个方格，他们的面积之和为40（1+1+4+9+25）。

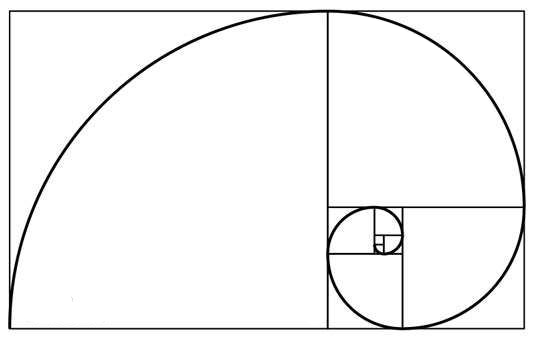
但是聪明的狗哥需要一个程序去获得指定范围内的螺旋线面积之和，狗哥给了你一首「希望之花」的时间，而他需要利用这个时间去打出四暗刻单骑。如果你能完成这个程序，狗哥会封你为格拉摩根伯爵

 

Input

不定组数据。

首先输入一个整数Q，代表狗哥询问次数。

接下来Q行，每行四个整数a,b,c,d，代表狗哥想求 a+b 到 c+d 之间的螺旋线面积之和。

1<= Q <= 10000

0<= a,c <= 10000

0 <= b,d <= 3

结果对192600817取模。

 

Output

一个数字，表示螺旋线面积之和。

 

Sample Input

4
0 0 0 1
0 0 1 0
1 2 2 1
1 1 0 3
4
0 0 0 1
0 0 1 0
1 2 2 1
1 1 0 3

 

Sample Output

2
40
4791
98
2
40
4791
98

题意: 求"a+b"到"c+d"以斐波那契数列为边长的正方形的面积之和,其中a或c是只有多少个4个正方形,b或d表示有b+1或d+1个正方形.如0+0是第一个正方形,0+1是第二个正方形,1+0是第五正方形.

简单的说就是"0+0","0+1","0+2","0+3","1+0"...的正方形.

注意:打表时需要每次都将矩阵初始化,否则上一次计算的结果会保留到下一次导致计算错误.

 

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define ll long long
 using namespace std;
 ll an[];
 ;
 struct Mat
 {
     ll m[][];
 } ans,A;;
 Mat mul(Mat A,Mat B)
 {
     Mat ret;
     ; i<; i++)
         ; j<; j++)
         {
             ret.m[i][j]=;
             ; k<; k++)
                 ret.m[i][j]=(ret.m[i][j]+((A.m[i][k])*(B.m[k][j]))%mod)%mod;
         }
     return ret;
 }
 Mat pow(Mat A,long long n)
 {
     Mat ret;
     ret.m[][]=;
     ret.m[][]=;
     ret.m[][]=;
     ret.m[][]=;
     while(n)
     {
         )
             ret=mul(ret,A);
         A=mul(A,A);
         n>>=;
     }
     return ret;
 }
 void init()
 {
     ans.m[][]=;
     ans.m[][]=;
     A.m[][]=;
     A.m[][]=;
     A.m[][]=;
     A.m[][]=;
 }
 int main()
 {
     int q,aa,bb,c,d;
     init();
     an[]=;
     ; i<; i++)
     {
         init();///每次计算时记得初始化矩阵
         ans=mul(ans,pow(A,i-));
         an[i]=an[i-]+ans.m[][]*ans.m[][];
     }
     while(cin>>q)
     {
         while(q--)
         {
             cin>>aa>>bb>>c>>d;
             ll st=*aa+bb+,ed=*c+d+;
             if(st>ed)swap(st,ed);
             printf(]);
         }
     }
 }